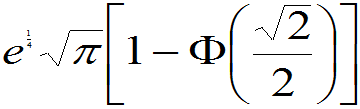三.连续性随机变量
1.联合概率密度
定义3.3 设(X,Y)的联合分布函数为F(x,y),若存在非负函数f(x,y),使得对于任意的实数x,y均有
F(x,y)=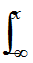
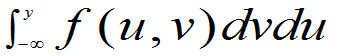 (3.12)
(3.12)
则称(X,Y)为连续型随机变量,并称f(x,y)为(X,Y)的联合概率密度,简称为概率密度。
2.f(x,y)有如下性质:
性质1 f(x,y)³0
性质2 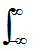
 =1
=1
性质3 若f(x,y)的连续点(x,y)处,有
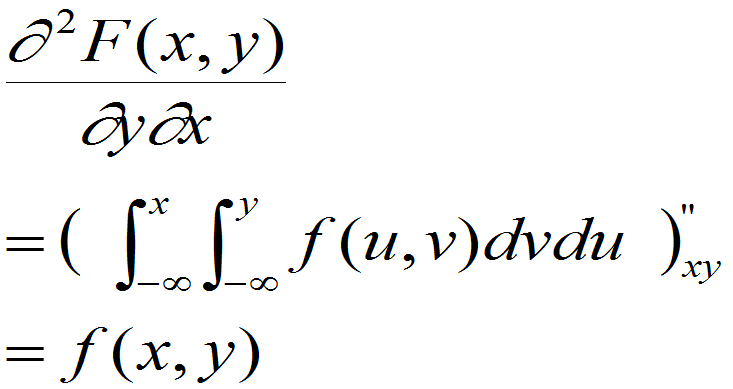
性质4 若随机点(X,Y)落于平面上相当任意的区域D内记为(X,Y)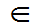 D,则
D,则
P{(X,Y)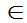 D}=
D}=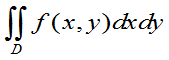 (3.16)
(3.16)
注:在f(x,y)非0域与D公共部分积分有非0值。
P71例2
例3:(第一版书上例3.3) 设(X,Y)的联合概率密度为
f(x,y)=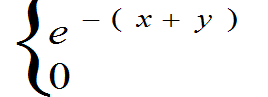

求(1)(X,Y) 的联合分布函数F(x,y);
(2) P{X>1}
(3)P{(X,Y)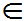 D},其中D={(x,y):x+y£1};
D},其中D={(x,y):x+y£1};
(4)P{X2³Y}
解:注意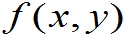 的非零域为H
的非零域为H
(1)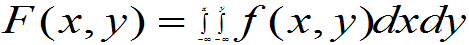 ,当
,当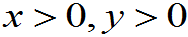
时,
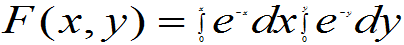

其他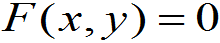
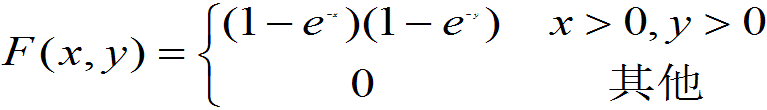
(2)P{X>1}=1- P{X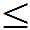 1}=1-Fx(1)=1- F(1,+
1}=1-Fx(1)=1- F(1,+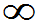 )
)
=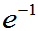
(3) P{(X,Y)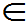 D}=
D}=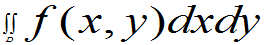
=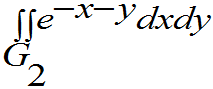 =
=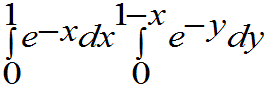
=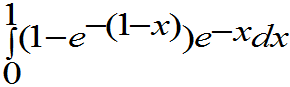
=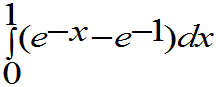
=
(4) P{X2³Y}=
=  =
=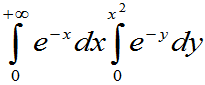
=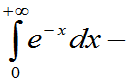
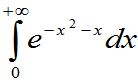
=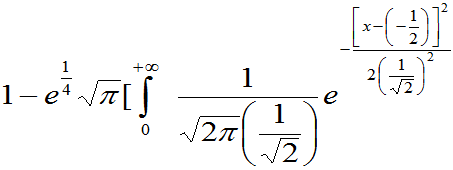 ]
]
注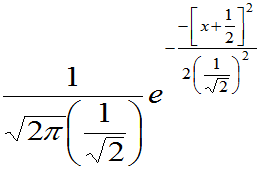 是
是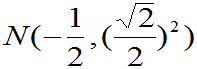 的概率密度,即
的概率密度,即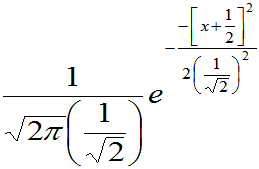 =
=
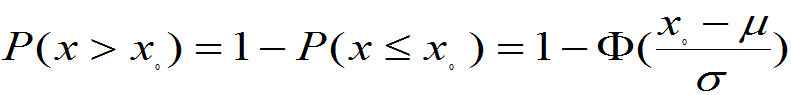
可知
 P{X2³Y}=1-
P{X2³Y}=1-