§2.4 连续型随机变量
- 定义2.2
设随机变量X的分布函数为F(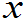 ),如果存在一个非负可积函数f(
),如果存在一个非负可积函数f( ),使对任意的实数
),使对任意的实数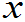 ,均有
,均有
F(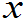 )=
)= (2.20)
(2.20)
则称X是连续型随机变量,称f(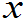 )是X的概率密度或密度函数,简称密度。
)是X的概率密度或密度函数,简称密度。
二、图形
例如:正态分布
密度函数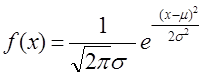 图形:
图形:
data normal;
do i=-3 to 3 by 0.01;
z0=exp(-i**2/2)/sqrt(2*(3.1415926));
output;
end;
run;
proc gplot data=normal;
plot z0*i=1 ;
symbol1 v=none i=join r=1 c=black;
run;
分布函数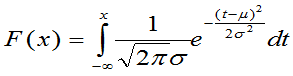 图形:
图形:
data normal;
do x=-3 to 5 by 0.01;
y=PROBNORM(x);
output;
end;
run;
proc gplot data=normal;
plot y*x=1 ;
symbol1 v=none i=join r=1 c=black;
run;
三、性质
性质1 f(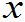 )
)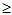 0 (2.21)
0 (2.21)
性质2
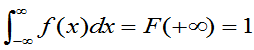 (2.22)
(2.22)
性质3 P(a<X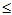 b)=F(b)-F(a)
b)=F(b)-F(a)
= 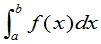 (2.23)
(2.23)
性质4
在f(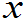 )的连续点
)的连续点 处,有
处,有
 =
=
 (2.24)
(2.24)
性质5
在f(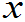 )的连续点
)的连续点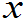 处,当
处,当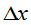 >0,且很小时,有
>0,且很小时,有
P(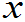 <X)=
<X)= 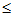
 +
+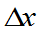
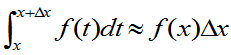
几点说明:
- 由5可以看出f(
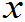 )值的大(小)反映R.V.X在
)值的大(小)反映R.V.X在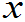 邻域概率的大(小)。
邻域概率的大(小)。
- 连续型随机变量X取任一点
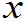 0的概率为零。即:P(X=
0的概率为零。即:P(X=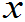 0)=0。
0)=0。
- 连续型随机变量X的密度函数为f(
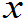 ),则它取值于区间(a,b)、(a,b]、[a,b)、[a,b]上的概率都相等,即
),则它取值于区间(a,b)、(a,b]、[a,b)、[a,b]上的概率都相等,即

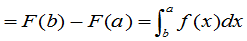
同理,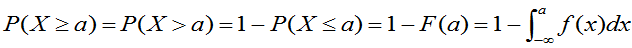 。
。
4.连续型R.V.X的F( )是连续函数。但f(
)是连续函数。但f(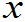 )不一定是连续的。
)不一定是连续的。
例1:(P51)设计R.V.X具有概率密度
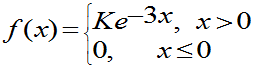
确定常数K,并求P{X>0.1}
指数分布:
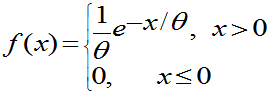
例:(第一版)设R.V.
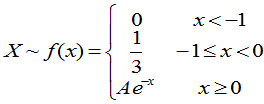
(1)确定常数A;(2)写出X的分布函数F(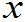 ); (3)P
); (3)P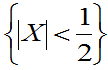 。
。
例:(第一版) 已知随机变量
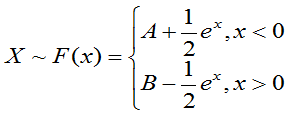
- 确定A和B;(2)求
 ;(3)求
;(3)求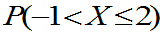
二、均匀分布
例:设R.V.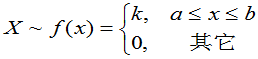 ,称X在[
,称X在[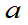 ,b]上服从均匀分布。(1)确定k。(2)求P(a<X
,b]上服从均匀分布。(1)确定k。(2)求P(a<X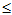 a+s)(a<a<a+s<b)。(3)写出X的分布函数F(
a+s)(a<a<a+s<b)。(3)写出X的分布函数F(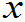 )。
)。
定义:若随机变量X的概率密度为

则称X在[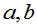 ]上服从均匀分布,记为X~U[a,b]
]上服从均匀分布,记为X~U[a,b]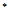 ,相应的分布函数为
,相应的分布函数为
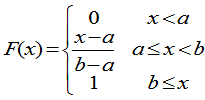
一般地,设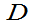 是轴上一些不相交的区间之和,若
是轴上一些不相交的区间之和,若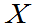 的概率密度为
的概率密度为

则称X在D上服从均匀分布。
如果 ,则对于满足
,则对于满足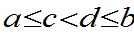 的任意的
的任意的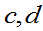 ,有
,有
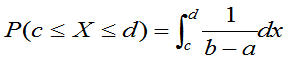 =
= (2.32)
(2.32)
三、指数分布
若随机变量X的概率密度为
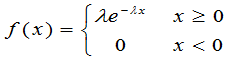 (2.33)
(2.33)
其中常数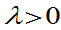 ,则称X服从参数为l的指数分布,相应的分布函数为
,则称X服从参数为l的指数分布,相应的分布函数为
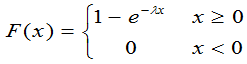 (2.34)
(2.34)
例:(第一版书上例2.12)
经过长期的观测,对某些电子元件的寿命可作如下假定:在已使用了th的条件下,在以后的Dth内损坏的概率为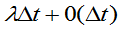 ,其中l是不依赖于t的常数;电子元件寿命为零的概率是零,求电子元件在内损坏的概率。略
,其中l是不依赖于t的常数;电子元件寿命为零的概率是零,求电子元件在内损坏的概率。略
四、正态分布
1、定义: 若随机变量X的概率密度为
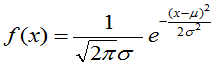 ,
, 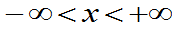 (2.35)
(2.35)
其中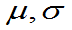 都为常数且
都为常数且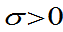 ,则称X服从参数为
,则称X服从参数为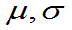 的正态分布,记为
的正态分布,记为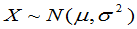 ,有时也简称X为正态随机变量。X的分布函数为
,有时也简称X为正态随机变量。X的分布函数为
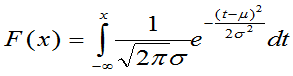 (2.36)
(2.36)
- 验证


- 作出
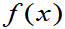 的图形
的图形
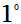
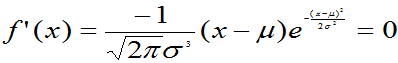 ,得驻点
,得驻点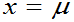 ,
,

 得
得 ,
,
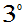

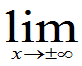



作图SAS程序:
data normal;
do i=-3 to 3 by 0.01;
z0=exp(-i**2/2)/sqrt(2*(3.1415926));
output;
end;
run;
proc gplot data=normal;
plot z0*i=1 ;
symbol1 v=none i=join r=1 c=black;
run;
注意:一定要和由正态随机数区别开来。如下面产生的是正态随机数。
data normal;
retain _seed_ 0;
do _i_ = 1 to 1000;
z = 0 + 1 * rannor(_seed_);
output;
end;
drop _seed_ ;
run;
proc gplot data=normal;
plot z*_i_=1 ;
symbol1 v=none i=join r=1 c=black;
run;
- 性质:
- f(x)的图形是关于直线x=m对称的曲线
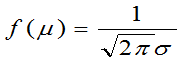 为最大值,当x远离m时,f(x)®0
为最大值,当x远离m时,f(x)®0
- 当m固定而s变化时对图形的影响,s
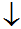
 小
小
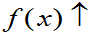 大,分布曲线在
大,分布曲线在 形成陡峭的高峰。
形成陡峭的高峰。
s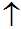 大
大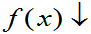 小,分布曲线在
小,分布曲线在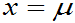 变成缓峰。
变成缓峰。
m=2, s=0.5, 1, 2
data normal;
do i=-2 to 6 by 0.01;
z0=exp(-(i-2)**2/2)/sqrt(2*(3.1415926));
z1=exp(-(i-2)**2/(2*0.25))/(0.5*sqrt(2*(3.1415926)));
z2=exp(-(i-2)**2/(2*4))/(2*sqrt(2*(3.1415926)));
output;
end;
proc gplot data=normal;
plot z0*i=1 z1*i=1 z2*i=1 /overlay ;
symbol1 v=none i=join r=1 c=black;
run;
m=2, s=0.5, 1, 2, 5, 10图形:
data normal;
do i=-5 to 9 by 0.01;
z0=exp(-(i-2)**2/2)/sqrt(2*(3.1415926));
z1=exp(-(i-2)**2/(2*0.25))/(0.5*sqrt(2*(3.1415926)));
z2=exp(-(i-2)**2/(2*4))/(2*sqrt(2*(3.1415926)));
z3=exp(-(i-2)**2/(2*25))/(5*sqrt(2*(3.1415926)));
z4=exp(-(i-2)**2/(2*100))/(10*sqrt(2*(3.1415926)));
output;
end;
run;
proc gplot data=normal;
plot z0*i=1 z1*i=1 z2*i=1 z3*i=1 z4*i=1 /overlay ;
symbol1 v=none i=join r=1 c=black;
run;
- 当s固定而当m变化时对图形的影响是分布曲线形状不变,仅曲线左、右平移。
如图:s=1, m=0, 2
data normal;
do i=-3 to 5 by 0.01;
z0=exp(-i**2/2)/sqrt(2*(3.1415926));
z1=exp(-(i-2)**2/2)/sqrt(2*(3.1415926));
output;
end;
run;
proc gplot data=normal;
plot z0*i=1 z1*i=1/overlay ;
symbol1 v=none i=join r=1 c=black;
run;
分布函数图:
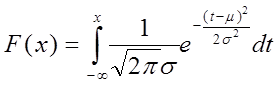
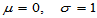
data normal;
do x=-5 to 10 by 0.01;
y=PROBNORM(x);
output;
end;
run;
proc gplot data=normal;
plot y*x=1 ;
symbol1 v=none i=join r=1 c=black;
run;




