§2.1 随机变量
- 概念
对于随机试验:
E | 甲,乙两人同时向某目标射击一次 |
中靶情况 |
|
E:  ,X表示射击中靶的次数,对应的取值为;0,1,2。
,X表示射击中靶的次数,对应的取值为;0,1,2。
定义:随机变量是定义在样本空间S={ω}上的一个单值实函数,记作X=X(ω),简记为X。
- 分类
- 离散型随机变量
- 非离散型随机变量
§2.2 离散型随机变量
一.离散型随机变量的分布
 设离散型随机变量可能取的值为:
设离散型随机变量可能取的值为: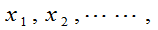
 取这些值的概率为
取这些值的概率为
 P(X=
P(X=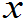 i)= pi ,i=1,2,... (2.1
i)= pi ,i=1,2,... (2.1 )
)
称(2.1)式为离散型随机变量X的 分布律。(2.1)式也可以用表格的形式表示如下:
分布律。(2.1)式也可以用表格的形式表示如下:
X |
|
| … |
| … |
P |
|
| … |
| … |
上述表格称为离散型随机变量X的分布列,分布列也可以表示成下列矩阵的形式:
离散型随机变量的分布律,分布列(以及下一节介绍的分布函数)统称为离散型随机变量的概率分布,简称为离散型随机变量的分布。
根据概率的性质,可知离散型随机变量的分布律具有下列性质
(1)pi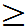 0,i=1,2,...
0,i=1,2,...
(2)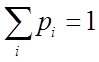
常见的几种分布
- 单点分布
例: 若随机变量X只取一个常数值C,即P(X=C)=1,则称X服从单点分布。(也叫退化分布。)
2、0-1分布
例: 若随机变量X只能取两个数值0或1,其分布为
X | 0 | 1 |
P | q | p |
0<p< 1,q=1-p,或记为P(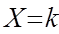 )=pkq1-k ,k=0,1
)=pkq1-k ,k=0,1
则称X 服从参数为p 的两点分布或参数为p的0-1分布。
- 几何分布
例: 一射手每次打靶射击一发子弹,打中的概率为p(0<p<1),不中的概率为q=1-p.今向靶作独立重复射击,直到中靶为止,则消耗的子弹数X 是一个离散型随机变量,其分布为
X | 1 | 2 | 3 | … | k | … |
P | p | qp | q2p | … | qk-1p | … |
或记为
 (
(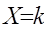 )=
)=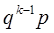 , k=1,2, ...
, k=1,2, ...
则称X服从参数为p的几何分布。
4、超几何分布
例:
设一批同类型的产品共有N件,其中次品有M件。今从中任取n(假定n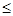 N-M)件,则这n件中所含的次品数X是一个离散型随机变量,其分布为
N-M)件,则这n件中所含的次品数X是一个离散型随机变量,其分布为
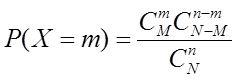 ,m=0,1…,k,k=min(M,n)
,m=0,1…,k,k=min(M,n)
则称X服从超几何分布。
- 二项分布
在n重伯努利试验中,事件A发生的次数X是一个离散型随机变量,其分布为
P( X= k )=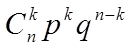 ,k=0,1,2,¼,n,称X服从参数为n,p的二项分布。记为
,k=0,1,2,¼,n,称X服从参数为n,p的二项分布。记为
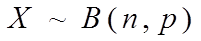 。
。
例2:P39.
例3:P40.
在电脑上,应用相应的数学或统计分析软件,这些概率是很容易计算出来的,所以,还有必要用逼近的方法吗?


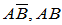

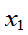
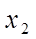
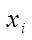
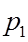
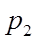

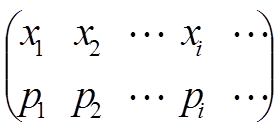


 浙公网安备 33010602011771号
浙公网安备 33010602011771号