确定现象:在一定条件下必然发生的现象,如向上抛一石子必然下落,等
随机现象:称某一现象是"随机的",如果该现象(事件或试验)的结果是不能确切地预测的。
由此产生的概念有:随机现象,随机事件,随机试验。
例:有一位科学家,他通晓现有的所有学科,如果对一项试验(比如:掷硬币),该万能科学家也无法确切地预测该实验的结果(是正面朝上还是反面朝上),这一实验就是随机实验,其结果是"随机的"----为一随机事件。
例:明天下午三点钟"深圳市区下雨"这一现象是随机的,其结果为随机事件。
随机现象的结果(随机事件)的随机度如何解释或如何量化呢?
这就要引入"概率"的概念。
概率的描述性定义:对于一随机事件A,用一个数P(A)来表示该事件发生的可能性大小,这个数P(A)就称为随机事件A发生的概率。
§1.1 随机试验
序号 | 条件 | 观察特性 | 可能结果 |
E1 | 抛一枚硬币 | 正、反面出现的情况 | 正面H,反面T |
E2 | 将一枚硬币抛掷三次 | 正、反面出现的情况 | HHH,HHT,HTH,THH,HTT,THT,TTH,TTT |
E3 | 同上 | 出现正面的次数 | 0,1,2,3 |
E4 | 抛一颗骰子 | 出现的点数 | 1, 2, 3, 4,5,6 |
E5 | 记录电话交换机呼唤次数 | 一分钟内接到的呼唤次数 | 0,1,2,3,…. |
E6 | 一批灯泡中任抽取一次 | 测量使用寿命 |
|
E7 | 记录某地昼夜温度 | 最高和最低温度 |
|
以上试验的共同特点是:
1.试验可以在相同的条件下重复进行;
2.试验的全部可能结果不止一个,并且在试验之前能明确知道所有的可能结果;
3.每次试验必发生全部可能结果中的一个且仅发生一个,但某一次试验究竟发生哪一个可能结果在试验之前不能预言。
我们把对随机现象进行一次观察和实验统称为随机试验,它一定满足以上三个条件。我们把满足上述三个条件的试验叫随机试验,简称试验,记E。
§1.2样本空间与随机事件
(一) 样本空间与基本事件
E的一个可能结果称为E的一个基本事件,记为ω,e等。
E的基本事件全体构成的集,称为E的样本空间,记为S或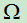 ,
,
即:S={ω|ω为E的基本事件},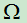 ={e}.
={e}.
注意:ω的完备性,互斥性特点。
例:§1.1中试验 E --- E7
--- E7
E :S
:S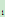 ={H,T}
={H,T}
E :S
:S ={ HHH,HHT,HTH,THH,
={ HHH,HHT,HTH,THH,
HTT,THT,TTH,TTT }
E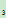 :S
:S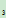 ={0,1,2,3}
={0,1,2,3}
E :S
:S ={1,2,3,4,5,6}
={1,2,3,4,5,6}
E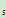 : S
: S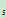 ={0,1,2,3,…}
={0,1,2,3,…}
E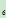 :S
:S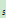 ={t
={t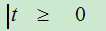 }
}
E7:S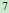 ={
={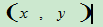
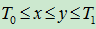 }
}
(二) 随机事件
我们把试验E 的全部可能结果中某一确定的部分称为随机事件。记为 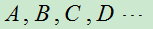
事件是由基本事件组成的,事件是样本空间的子集。
集合论 | 集合 点 子集 |
概率论 | S |
在一次试验中,事件A 发生的含义是,当且仅当A 中的某一个基本事件发生。事件A 发生也称为事件A 出现。
必然事件:S
不可能事件: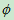
例1.(P4) 在E2中事件A1:"第一次出现是的H",
即:
(三) 事件的关系与运算
设E 的S ,A ,B,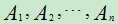
1.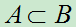
2.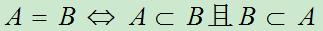
3.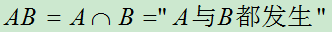
4.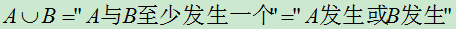
5.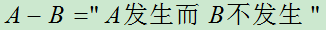
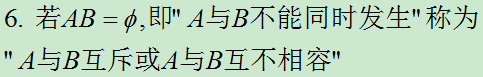
7.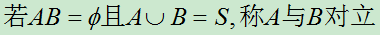 。
。
记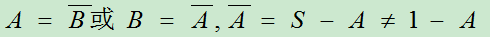 。
。
(常用的关系) 补充
1.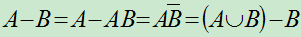
2.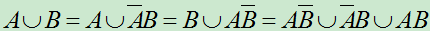
3.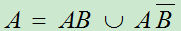
吸收律
若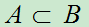 ,则
,则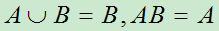
特别注意: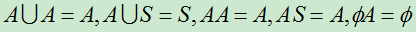
德·莫根律(对偶公式)
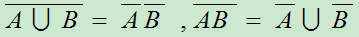
推广: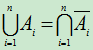 ,
,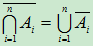 。
。
例2:P6,在例1中….
其它例子:
例3: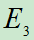 :设
:设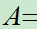 {甲中},
{甲中},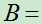 {乙中},问
{乙中},问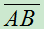 与
与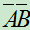 各表示什么事件?是否是相等事件?
各表示什么事件?是否是相等事件?
留为练习
例4:一射手向目标射击3发子弹,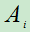 表示第i次射击打中目标
表示第i次射击打中目标 。试用
。试用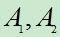 及
及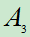 其运算表示下列事件:
其运算表示下列事件:
(1)"三发子弹都打中目标";
(2)"三发子弹都未打中目标";
(3)"三发子弹至少有一发打中目标";
(4)"三发子弹恰好有一发打中目标";
(5)"三发子弹至多有一发打中目标".
留为练习
§1.3 概率与频率
- 事件的频率及其稳定性
设某试验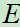 的样本空间为
的样本空间为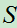 ,
,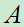 为E的一个事件。把试验E重复进行了n次,在这n次试验中,A发生的次数
为E的一个事件。把试验E重复进行了n次,在这n次试验中,A发生的次数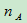 称为A的频数。称
称为A的频数。称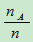 为事件A在n次试验中发生的频率,记作:
为事件A在n次试验中发生的频率,记作:
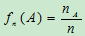 。
。
频率的基本性质
- 对任意事件A,有
 ;
;
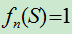 ,
, ;
;
- 若
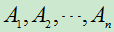 是互不相容的,则
是互不相容的,则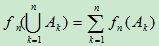 ,
,
推论:对任一事件A,有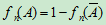 。
。
实践证明:当试验次数n很大时,事件A的频率 几乎稳定地接近一个常数p。频率的这种性质称为频率的稳定性,它是事件本身所固有的。书上p8—9页例1,2.
几乎稳定地接近一个常数p。频率的这种性质称为频率的稳定性,它是事件本身所固有的。书上p8—9页例1,2.
概率的频率定义
定义1.1 在一组不变的条件下,重复作n次试验,记m是n次试验中事件A发生的次数。当试验次数n很大时,如果频率 稳定地在某数值p附近摆动,而且一般地说,随着试验次数的增加,这种摆动的幅度越来越小,则称数值p为事件A在这一组不变的条件下发生的概率,记作
稳定地在某数值p附近摆动,而且一般地说,随着试验次数的增加,这种摆动的幅度越来越小,则称数值p为事件A在这一组不变的条件下发生的概率,记作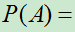 p。
p。
补充:概率的几种度量方法
事件A的概率,记为P(A),表示该事件发生的可能性大小,是事件的一个非负实值函数,满足某种概率进行代数运算的公理。
对概率P(A)有几种不同的度量方法:
前面给出了用频率度量概率的方法,也称为古典概率度量。还是二种度量方法。
- 几何概率度量

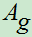 表示"在区域
表示"在区域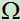 中随机取一点,而该点落在区域g中"这一事件。
中随机取一点,而该点落在区域g中"这一事件。
 例:
例:


这时, 可以是整个园:测度为面积;也可以是整个园周:测度为长度。
可以是整个园:测度为面积;也可以是整个园周:测度为长度。
- 主观概率度量
对事件A的信念度称为这一事件的概率P(A).
主观概率(信念度)是通过相对似然的概念来运算的。
例如:见朱手稿。。。
现通过例子说明此方法:
例1:事件A"明天下午3点深圳市区有雨",
求P(A): 即求A的主观概率;
现有一大转盘,标有红色区域,事件B:"指针落在红色区域"。
让你选择A发生还是B发生的可能性大,为了迫使你选择,有这样的将励机制,。。。选择对的话,将10万元。。。


 红色区域
红色区域
如果开始时,红色区域充满整个园,你当然要选B发生的可能性大,逐步调节红色区域的大小,渐渐缩小,。。。等到选A或B都一样时停止,这时,可以由B的几何概率作为A的主观概率。
当你对选A或B谁发生的可能性大没有偏好时,。。。
例2. 假如你面临以下两种选择:1.如果事件A发生,你将得到少量的报酬R;否则没有报酬。2.参加抽奖,你赢得一份小报酬R的概率为P,但是你输或者说你得不到报酬的概率为1-P。
如果你对1,2两种选择没有偏好,那么你判断事件A发生的概率为P.(主观)
(二) 概率的公理化定义
概率的公理化定义
定义1.2 设试验E的样本空间为S,如果对每一个事件A都有一个实数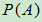 与之对应,且满足下面三条公理:
与之对应,且满足下面三条公理:
公理1(非负性):对任一事件A,有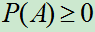 ;
;
公理2(规范性):对必然事件S,有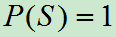 ;
;
公理3(完全可加性)若可列无穷多个事件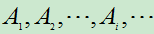 互不相容,则
互不相容,则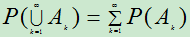 ,那么称
,那么称 为事件A的概率。
为事件A的概率。
概率的性质
(1)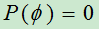 ;
;
(2)有限可加性: 若 互不相容,则
互不相容,则 ;
;
(3)对事件A,都有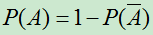 ;
;
- 若
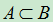 ,则
,则 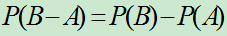 ;
;
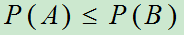 ;
;
特别的,对任何事件A,都有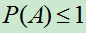 ;
;
- 对任何两个事件A,B,都有
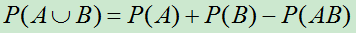 ;
;
- 对任何n个事件
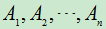 ,都有
,都有
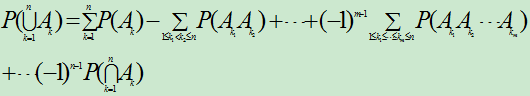
例10---12为第一版上的例子。
例10: A,B是E中二个事件,已知
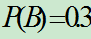 ,
,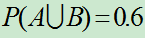 ,求
,求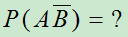
解: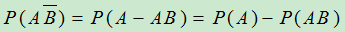

例11:在某城市的居民中订购报纸的情况是:订购A报的占45%,订购B报的占35%;订购C报的占30%,同时订购A,B的占10%,同时订购A,C的占8%,同时订购B,C的占5%,同时订购A,B,C的占3%。求下列事件的概率(百分率)
(1){只订购A报纸的};(2){至少订一种报纸的}。
例12:在所有的两位数(即从10至99)中,
任取一个数,求这个数能被2或者3整除的概率。
§1.4 等可能概型(古典概型)
一、古典概率
1.古典概型与计算公式
E满足:
① S中基本事件ω个数是有限的n ;
② 每个基本事件发生是等可能的.
称E为古典概型。
E中事件A包含k个基本事件,则A发生的概率为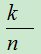
 P(A).
P(A).
2.古典概率的基本性质
设E是古典概型,其样本空间为 ,A,A
,A,A ,A
,A ,…,A
,…,A 是E中事件:
是E中事件:
①.0≤P(A)≤1
②.P(S)=1,P( )=0
)=0
③.若A ,A
,A ,…,A
,…,A 是互不相容的事件,则有P
是互不相容的事件,则有P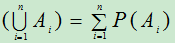 ;
;
推论: P(A)=1- P( )。
)。
- P13,将一枚硬币掷三次,。。。。
P14---17 例2—7.照书上讲。。。
以下例4---9为第一版上的例子:
例4:E 中求任取一球的号码为偶数的概率。
中求任取一球的号码为偶数的概率。
解:设A={所取的球的号码为偶数}={ w2,w4,w6 }
即A中基本事件数k=3,于是P(A)= .
.
例5:(1.10)在一袋中有10 个相同的球,分别标有号码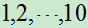 。每次任取一个球,记录其号码后放回袋中,再任取下一个。这种取法叫做"有放回抽取"。今有放回抽取3个球,求这3个球的号码均为偶数的概率。
。每次任取一个球,记录其号码后放回袋中,再任取下一个。这种取法叫做"有放回抽取"。今有放回抽取3个球,求这3个球的号码均为偶数的概率。
例6:(1.11) 在一袋中有10 个相同的球,分别标有号码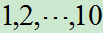 。每次任取一个球,记录其号码后不放回袋中,再任取下一个。这种取法叫做"不放回抽取"。今不放回抽取3个球,求这3个球的号码均为偶数的概率。
。每次任取一个球,记录其号码后不放回袋中,再任取下一个。这种取法叫做"不放回抽取"。今不放回抽取3个球,求这3个球的号码均为偶数的概率。
例7:盒中有a个红球,b个白球(a≥2 , b≥1),
每次从中任取一球,不放回地连取三次,求下列事件的概率:
(1) " 取出的三个球依次为红,白,红色球 "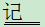 A ;
A ;
(2)" 取出的三个球有两个是红色球 "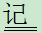 B .
B .
例:(1.13) 在一袋中有10 个相同的球,分别标有号码 。今任取两个球,求取得的第一个球号码为奇数,第二个球号码为偶数的概率。
。今任取两个球,求取得的第一个球号码为奇数,第二个球号码为偶数的概率。
例8:(1.14)设一批同类型的产品共有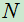 件,其中次品有
件,其中次品有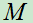 件。今从中任取
件。今从中任取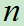 (假定
(假定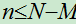 )件,求次品恰有
)件,求次品恰有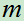 件的概率
件的概率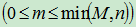
例9:一箱内装有同类产品六件(其中4件是正品,二件是次品)。从中每次取一件,连取两次。求下列事件的概率:
(1)" 取到的两件产品的质量是相同的 " A ;
A ;
(2)"取到的两件产品至少有一件是正品" B .
B .
§1.5 条件概率
条件概率
- 条件概率
例1 将一枚硬币抛掷两次,观察其出现正反面的情况,设事件A为"到少有一次为H", 事件B为"两次掷出同一面"。现在来求已知事件A已经发生的条件下事件B发生的概率。
解:样本空间为S={HH,HT,TH,TT},
A={HH,HT,TH}, B={HH,TT}
于是在A发生的条件下B发生的概率(记为P(B/A))为:
P(B/A)=1/3
注意到:
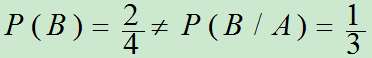
易知:

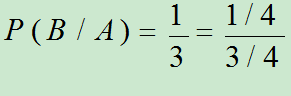
- 定义:设A,B为E中的二个事件,且
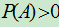 ,则在事件A已发生的条件下,事件B发生的条件概率定义为:
,则在事件A已发生的条件下,事件B发生的条件概率定义为: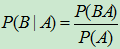 .同样若
.同样若 ,则
,则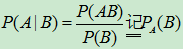 。
。
- 性质(定理)
如果
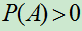 ,则
,则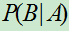 是概率.
是概率.
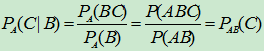
- 计算方法
法一:公式计算法;
法二:直接计算法.
不难验证,条件概率P(·/A)符合概率定义中的三个条件:
1.非负性
2.完全性
3.可加性
P19
例2 P19,。
下面的例11--13为第一版。
例11:甲乙二厂同生产一种零件,分放在二个箱内,它们产品的情况如下:
正品 | 次品 | 小计 | |
甲厂 | 50 | 20 | 70 |
乙厂 | 25 | 5 | 30 |
小计 | 75 | 25 | 100 |
从中任取一件产品,求下列事件的概率:
(1)"取得的一件产品是甲厂产品"=A;
(2)"取得的一件产品是次品"=B;
(3)"取得的一件产品是甲厂生产的次品";
(4)已知取得的一件产品是甲厂生产的,求它是次品的概率。
例12:在标号依此为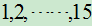 的15个同类球
的15个同类球
中,任取一球。易算出下列事件的概率和条件概率。
(1)取得"标号为偶数"(事件A)的概率;
(2)取得"标号小于6"(事件B)的概率;
(3)取得"标号既为偶数,又小于6"(事件AB)的概率;
(4)若已知"所取球的标号小于6"(即在B已发生的条件下),则"球的标号为偶数"(即A再发生)的概率。
例13:(书例1.20) 设有100件同类型的产品,其中80件一等品,15件二等品,5件次品。从中任取一件,已知"取得的是非次品"(事件B),求"它是一等品"(事件A)的概率。
(二)概率的乘法公式
定义: 设两个事件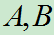 ,且
,且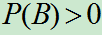 ,由条件概率公式得
,由条件概率公式得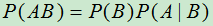 ,若
,若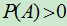 ,有
,有 称为概率的乘法公式(定理).
称为概率的乘法公式(定理).
例3,4,P21---22;
例14
—16为第一版:例14: (书例1.21) 10件同类型产品,其中8件正品,2件次品。今不放回抽取两次,每次取一件,求"两件均为正品"(事件A)的概率。
推广:对n个事件 ,且
,且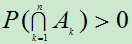 ,则有
,则有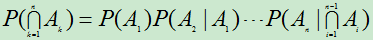 。
。
例15: (书例1. 22) 一城市位于甲,乙两河的汇合处,当两河流至少有一泛滥时,该市就会被淹,已知在指定的时间内,甲,乙两河泛滥的概率均为0.01,又当甲河泛滥时引起乙河泛滥的概率为0.5。求在指定的时间内该市被淹的概率。
例: 已知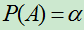 ,
,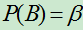 ,
,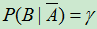 ,且
,且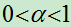 ,
,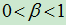 。求:
。求: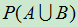 ;
; 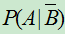 。
。
例16:十个人抓一张电影票,问每个人抓到电影票的概率与抽签的次序是否有关?
条件概率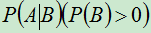 与
与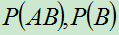 有如下的一般关系
有如下的一般关系
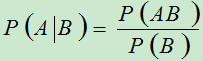
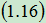
(三)全概率公式
例17(第一版):口袋中有16个球,其中白球10个,红球6个。每次取一球,取后不放回,连取两次。求下列事件的概率:
(1)"第一次,第二次取的都是白球";
(2)"第二次才取到白球";
(3)"第二次取到白球".
思考:三个事件有什么不同?
第(3)个事件有何特点?难点在哪?怎么解决问题?
定理1.1(全概率公式)
若事件组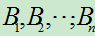 满足:
满足:
(1) 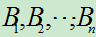 互不相容且
互不相容且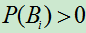 ,
,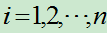 ,
,
(2)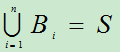 ;
;
则对任何事件A,均有
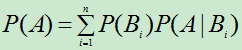 。 (1.19)
。 (1.19)
称满足(1)、(2)的事件组为完备事件组。(1.19)式称为全概率公式。
重点在于:什么情况下用全概率公式,如何用全概率公式解决实际问题。关键是找出 且找出
且找出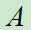 发生的"
发生的" 种可能原因"或"可能的前提条件"或"情况"将其视为
种可能原因"或"可能的前提条件"或"情况"将其视为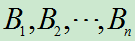 。
。
例18(第一版):(书例1.23) 市场出售的灯泡,甲厂占80%(其中合格率为95%),乙厂占20%(其中合格率为90%)。任买一灯泡,求它是合格品的概率。
例19(第一版):甲、乙、丙三厂生产一批同类产品。甲厂产量是乙厂、丙厂产量之和,而乙厂产量是丙厂产量的二倍。又知甲、乙、丙三厂产品的正品率分别为0.90,0.96,0.84。
- 求从该批产品中任取一件是正品的概率;
- 已知取得的一件是正品,问它是哪个厂产品的可能性最大(概率)?
(四) 贝叶斯公式
定理1.2 若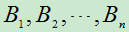 是一完备事件组,则对任意的事件
是一完备事件组,则对任意的事件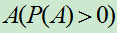 ,均有
,均有
 。
。
此式称为贝叶斯公式。
例6,7,P24页。
例20(第一版):(书例1.26) 某厂产品96%是(真)合格品。有一验收方法,把(真)合格品判为"合格品"的概率为0.98,把非合格品判为"合格品"的概率为0.05。求此验收方法判为"合格品"的一产品为(真)合格品的概率。
例21(第一版):袋中有n个球,其中白球数未知,假设有i个白球的可能性对所有的i=0,1,…,n都相等。现从袋中任取一球,求在取得的球是白球的条件下,袋中原来有i个白球的概率?(i=0,1,…,n)
§1.6 事件的独立性.伯努利概型
一.事件的独立性
1.两个事件A,B的独立性
定义1.3 对任意的事件A,B,若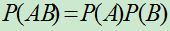 ,则称事件A,B是相互独立的。
,则称事件A,B是相互独立的。
性质1: 若A与B独立,则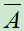 与B,A与
与B,A与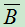 ,
,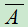 与
与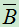 相互独立。
相互独立。
2.推广
定义1.4 对任意三个事件A,B,C,若

则称事件A,B,C相互独立,简称A,B,C独立。
一般的,对任意n个事件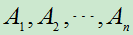 ,若
,若
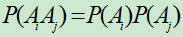 ,
,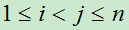 ;
;
 ,
, ;
;
…………………
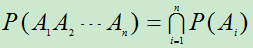 。
。
则称事件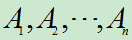 相互独立,简称
相互独立,简称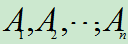 独立。
独立。
性质2:若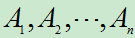 相互独立,则
相互独立,则
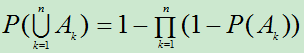 。
。
例22(第一版):(书例1.27) 甲,乙,丙三人同时独立向同一目标射击,他们射中目标的概率分别为0.4,0.5,0.7。求
- 至少有一人射中目标的概率;
- 恰有一人射中目标的概率。
例23(第一版): 袋中装有编号为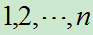
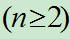 的n个球,有放回地抽r次,求:
的n个球,有放回地抽r次,求:
(1)1号球不被抽到的概率;
(2)1号球和2号球均被抽到的概率。
二.伯努利概型
- 若试验E只有两个可能结果A和
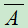 ,且
,且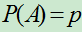 ,
,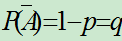 ,
,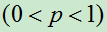 则称E为伯努利概型。
则称E为伯努利概型。
称A为"成功", 为"失败"。
为"失败"。
- n重伯努利试验
将伯努利试验E,在相同条件下,独立地重复进行n次,作为一个试验,则这个试验为n重伯努利概型。记为En。
注意两点:相同条件下,即每次
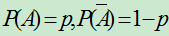 相同。
相同。
各次试验结果是独立的。
3. 定理1.3
设E为伯努利试验,且
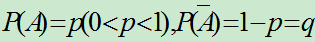 ,则在n重伯努利概型中,事件A恰好发生
,则在n重伯努利概型中,事件A恰好发生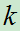 次的概率为:
次的概率为: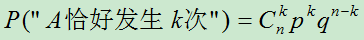 ,
,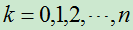 。
。
例2---3P27—28.
第一章作业:
设计一随机试验E,给该试验的样本空间S,基本事件ω,并给出一至二个事件。
习题1,2,17,18,20,26
例24(第一版):(书例1. 29) 某射手的命中率为0.9,他独立重复向目标射击5次,求恰好命中3次的概率。
例25(第一版).(书例1. 30) 设一批同类型的产品有N件,其中次品有M件。今从中有放回抽取n件,求次品恰有m件的概率。
§ 1—5几个例题(第一版)
例:(书例1.33)一袋中装有N-1只黑球和1只白球,每次从袋中随机地摸出一只球并放入一只黑球,这样继续下去,求第k次摸球时摸到黑球的概率。
例:(书例1.34)把7个编号的同类型的球扔进4个编号的盒子中,每个球被扔进任何一个盒子中都是等可能的。求第一个盒子恰有2个球的概率。
例:(书例1.37)甲,乙,丙三人同时独立向一飞机射击,他们设中飞机的概率分别为0.4,0.5,0.7。设若只有一人射中,飞机坠毁的概率为0.2;若恰有两人射中,飞机坠毁的概率为0.6;若三人均射中,飞机必然坠毁。求飞机坠毁的概率。若已知飞机坠毁,求它是恰有二人射中的概率。
例:(例1.38)设某型号的高射炮发射一发炮弹击中飞机的概率为0.6,现用此型号的炮若干门同时发射一发炮弹,问至少需配置几门高射炮才能以不小于0.99的概率击中来犯的一架敌机?
例:(例1.41)甲,乙二人进行棋类比赛。每次比赛没有和棋,甲赢的概率为p,乙赢的概率为q,p+q=1 ,赢者得1分,输者得0分。比赛独立地进行到有一人超过对方2分才结束,多得二分者为胜。求甲,乙获胜的概率各是多少。
例:(例1.42)甲,乙二人约定,将一枚匀称的硬币掷两次,若正面至少出现一次,则甲胜;否则乙胜。求甲胜的概率。


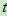

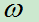 A
A

 浙公网安备 33010602011771号
浙公网安备 33010602011771号