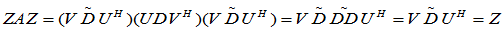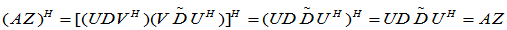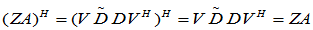第十三讲 Penrose 广义逆矩阵(I)
一、Penrose 广义逆矩阵的定义及存在性
所谓广义,即推广了原有概念或结果。我们知道,逆矩阵概念是针对非奇异的(或称为满秩的)方阵。故这一概念可推广到:(1)奇异方阵;(2)非方矩阵。事实上, Penrose广义逆矩阵涵盖了两种情况。
对于满秩方阵A, A 存在,且AA
存在,且AA =A
=A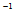 A=I 故,当然有
A=I 故,当然有
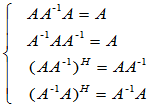

这四个对满秩方阵显然成立的等式构成了Penrose广义逆的启示。
- Penrose定义:设A
 C
C ,若Z
,若Z C
C 且使如下四个等式成立,
且使如下四个等式成立,
AZA = A, ZAZ = Z, (AZ)
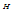 = AZ , (ZA)
= AZ , (ZA) = ZA
= ZA
则称Z为A的Moore-Penrose(广义)逆,记为,A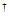 。
。
而上述四个等式有依次称为Penrose方程(i),(ii) ,(iii) ,(iv)。
- Moore-Penrose逆的存在性和唯一性
定理:任给A
 C
C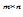 ,A
,A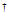 均存在且唯一。
均存在且唯一。
证明:存在性.
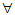 A
A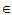 C
C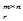 ,均存在酉矩阵U
,均存在酉矩阵U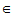 C
C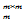 ,V
,V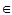 C
C 使
使
U
 AV = D =
AV = D =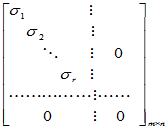 即 A = UDV
即 A = UDV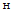
其中,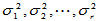 是A
是A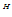 A的全部非零特征值。
A的全部非零特征值。
此时,令Z=V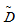 U
U
 C
C 则
则
 =
=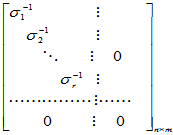
即,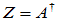
其中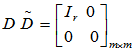
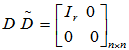
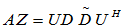 ,
, 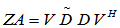
唯一性:设Z ,Y均满足四个Penrose方程,则
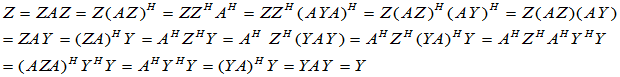 即,满足四个Penrose方程的Z是唯一的.
即,满足四个Penrose方程的Z是唯一的.
该证明实际上给出了Moore-Penrose逆的一种构造方法。由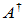 的唯一性可知:(1)当A 为满秩方阵时,
的唯一性可知:(1)当A 为满秩方阵时,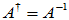 ; (2)
; (2) 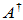 实际上还是一个限制相当严格,狭窄的量,可考虑更加放宽。
实际上还是一个限制相当严格,狭窄的量,可考虑更加放宽。
- {
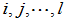 }-逆的定义:
}-逆的定义: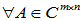 ,若
,若 且满足Penrose方程中的第
且满足Penrose方程中的第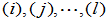 个方程,则称Z为A 的
个方程,则称Z为A 的 -逆,记为
-逆,记为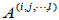 ,其全体记为
,其全体记为 。
。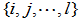 -逆共有
-逆共有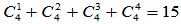 类,但实
类,但实
际上常用的为如下5类:A{1}, A{1,2}, A{1,3}, A{1,4}, A{1,2,3,4}=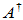
二、{1}-逆的性质
引理: 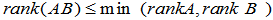
证明:矩阵的秩=行秩=列秩. 将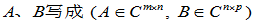
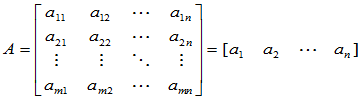
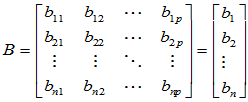
(1)设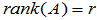 ,则必存在
,则必存在 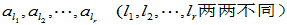 成为线性无关的向量组。所以,其它列向量
成为线性无关的向量组。所以,其它列向量 可表示为:
可表示为:
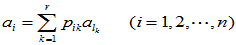

可见AB 的各列向量均为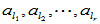 的线性组合。亦即
的线性组合。亦即
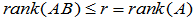
(2) 同理。设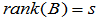 ,则必存在
,则必存在 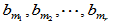 成为线性无关的向量组。所以,其它列向量
成为线性无关的向量组。所以,其它列向量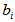 可表示为:
可表示为:
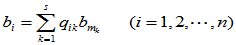
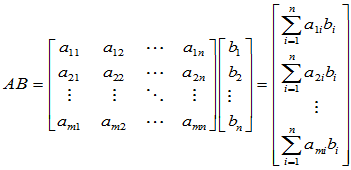
可见,AB的各行向量均为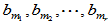 的线性组合,故
的线性组合,故
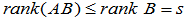
合起来即 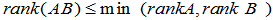
定理:设
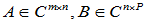 ,
, 则
则
(1) 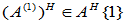
(2) 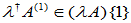
(3) S、T为可逆方阵且与A可乘,则
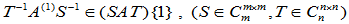
(4) 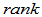 (
(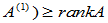
(5) 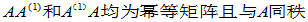 (
(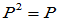 )
)
(6) 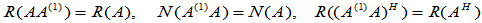
(7) 
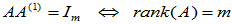
(8) 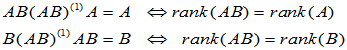
证明:(1) 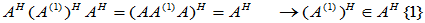
(2) 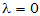 时,
时, ,
, .显然成立.
.显然成立.
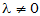 时,
时,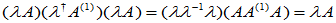
(3) 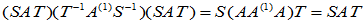
(4) 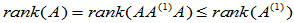
(5) 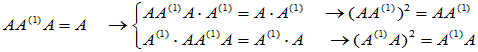
又 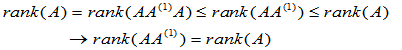
同理,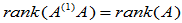
(6) 
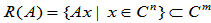 ,
,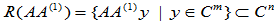
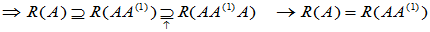
同理
又法:将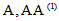 写成
写成
 均为m维列向量,则
均为m维列向量,则
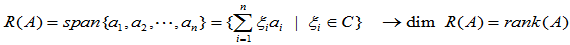
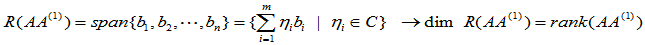 即
即 
故 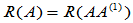
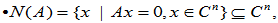
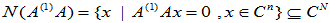
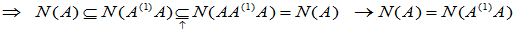
同理
又法: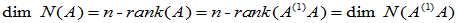
又 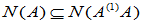 故
故 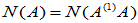
在 中,将
中,将 换为
换为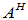 ,
,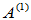 换为
换为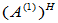 ,则有
,则有
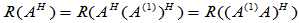
(7) 以  为例.
为例.
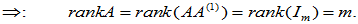
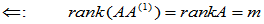
即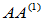 为m阶满秩可逆方阵,
为m阶满秩可逆方阵,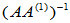 存在。
存在。
又  幂等:
幂等: 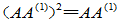 , 乘以
, 乘以 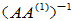 ,得
,得 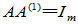
(8) 
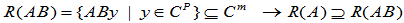
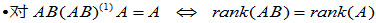
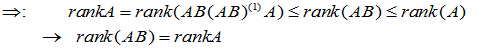
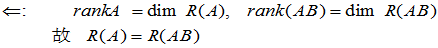
即,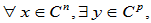 使
使 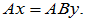 故
故
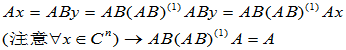
 对
对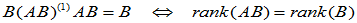
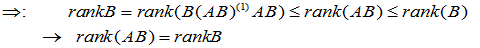
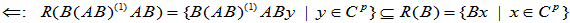
又,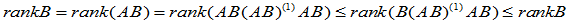

即,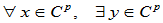 ,使
,使 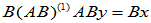 . 故
. 故

定理:矩阵A当且仅当A 为满秩方阵时具有唯一的{1}逆,此时
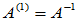
作业:P306 3,4,5