第十二讲 满秩分解与奇异值分解
一、矩阵的满秩分解
1. 定义:设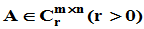 ,若存在矩阵
,若存在矩阵 及
及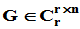 ,使得
,使得
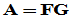 ,则称其为
,则称其为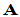 的一个满秩分解。
的一个满秩分解。
说明:(1)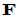 为列满秩矩阵,即列数等于秩;
为列满秩矩阵,即列数等于秩;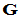 为行满秩矩阵,即行数等于秩。
为行满秩矩阵,即行数等于秩。
(2)满秩分解不唯一。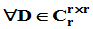 (
(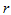 阶可逆方阵),则
阶可逆方阵),则
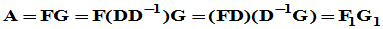 ,且
,且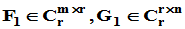
2. 存在性定理:任何非零矩阵均存在满秩分解
证:采用构造性证明方法。设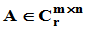 ,则存在初等变换矩阵
,则存在初等变换矩阵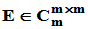 ,
,
使  , 其中
, 其中
将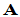 写成
写成 ,并把
,并把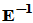 分块成
分块成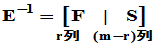 ,其中
,其中
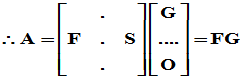 是满秩分解。
是满秩分解。
3. Hermite标准形(行阶梯标准形)
设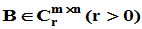 ,且满足
,且满足
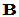 的前
的前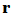 行中每一行至少含一个非零元素(称为非零行),且第一个非零元素为1,而后
行中每一行至少含一个非零元素(称为非零行),且第一个非零元素为1,而后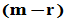 行的元素全为零(称为零行);
行的元素全为零(称为零行);
- 若
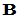 中第
中第 行的第一个非零元素(即1)在第
行的第一个非零元素(即1)在第 列
列 ,则
,则
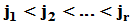 ;
;
- 矩阵
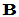 的第
的第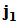 列,第
列,第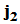 列,…,第
列,…,第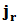 列合起来恰为
列合起来恰为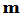 阶单位方阵
阶单位方阵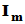 的前
的前 列(即
列(即 列上除了前述的1外全为0)则称
列上除了前述的1外全为0)则称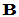 为Hermite标准形。
为Hermite标准形。
例1  为Hermite标准形
为Hermite标准形
 也是Hermite标准形
也是Hermite标准形
4. 满秩分解的一种求法
设 ,
,
- 采用行初等变换将
 化成Hermite标准形,其矩阵形式为
化成Hermite标准形,其矩阵形式为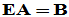 ,其中
,其中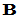 为Hermite标准形定义中给出的形状;
为Hermite标准形定义中给出的形状;
- 选取置换矩阵
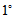
 的第
的第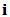 列为
列为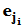 ,即该列向量除第
,即该列向量除第 个元素为1外,其余元素全为零
个元素为1外,其余元素全为零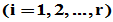 ;
;
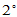 其它
其它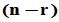 列只需确保
列只需确保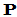 为置换矩阵即可(
为置换矩阵即可( 的每一行,每一列均只有一个非零元素,且为1);
的每一行,每一列均只有一个非零元素,且为1);
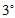 用
用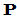 右乘任何矩阵(可乘性得到满足时),即可得该矩阵的第
右乘任何矩阵(可乘性得到满足时),即可得该矩阵的第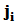 列置换到新矩阵(即乘积矩阵)的第
列置换到新矩阵(即乘积矩阵)的第 列
列
 令
令 ,即
,即
(3)令 的前
的前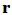 行
行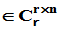 ,
, 则
则
证明: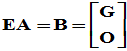 ,
, 则
则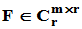 ,
,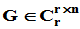 ,
, 已知,但
已知,但 ,当然可以通过求出
,当然可以通过求出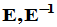 再将
再将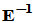 分块得到,但这样
分块得到,但这样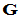 就没必要采用Hermite标准形形式,注意到
就没必要采用Hermite标准形形式,注意到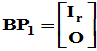 ,则
,则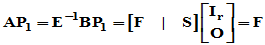 证毕
证毕
例1  求其满秩分解
求其满秩分解
解:(1)首先求出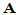 的秩。显然,前两列互相独立,而第三行可由第一行减去第二行得到,故
的秩。显然,前两列互相独立,而第三行可由第一行减去第二行得到,故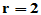 。
。
(2)进行初等变换将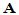 化为Hermite标准型。
化为Hermite标准型。

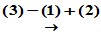

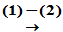

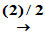
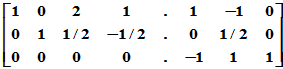 , 即
, 即
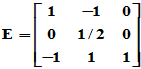 ,
,  ,
,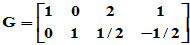
(3)求出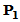 及
及
由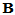 可见,
可见,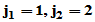 故
故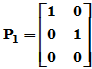 ,
,
验证:
而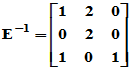
二、酉对角分解与奇异值分解
1. 厄米矩阵的谱分解
 为厄米矩阵,则存在酉矩阵
为厄米矩阵,则存在酉矩阵 ,使
,使

将 写成列向量形式,即
写成列向量形式,即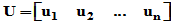 ,则
,则
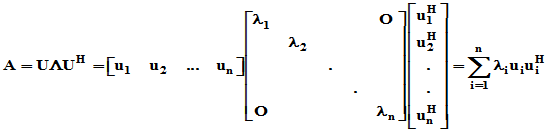
2. 非奇异矩阵的酉对角分解
定理:设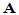 为
为 阶非奇异矩阵,则存在
阶非奇异矩阵,则存在 阶酉矩阵
阶酉矩阵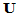 及
及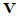 ,使得
,使得
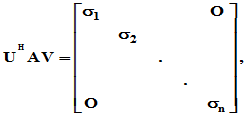
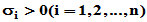
(若将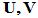 写成
写成
 ,则
,则 )
)
证: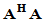 也为
也为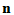 阶非奇异矩阵,而且是厄米,正定矩阵,故存在
阶非奇异矩阵,而且是厄米,正定矩阵,故存在 阶酉矩阵
阶酉矩阵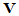 ,使
,使 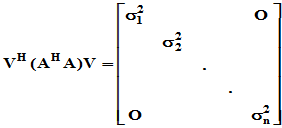
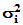 为
为 的特征值。
的特征值。
令 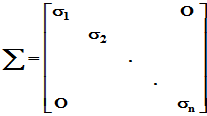 ,则
,则 
令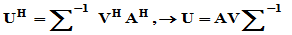 ,则
,则

即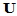 也是酉矩阵,而且
也是酉矩阵,而且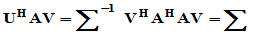 证毕
证毕
酉对角分解的求法正如证明中所给:先对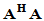 对角化(酉对角化),求出变换矩阵
对角化(酉对角化),求出变换矩阵 ,再令
,再令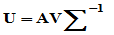 即可。
即可。
3. 一般矩阵的奇异值分解
定理:设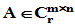 ,则存在
,则存在 阶酉矩阵
阶酉矩阵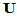 及
及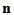 阶酉矩阵
阶酉矩阵 ,使
,使
 即
即

证:首先考虑 。因为
。因为 ,故
,故 ,
,
而且是厄米,半正定的,存在 阶酉矩阵
阶酉矩阵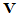 ,使
,使
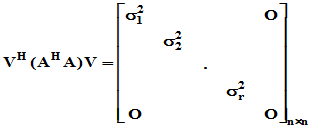
令 ,
,  则
则
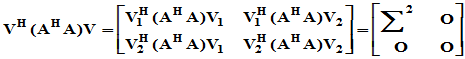

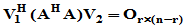
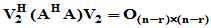
令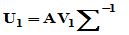 则
则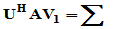 ,又
,又
在 的基础上构造酉矩阵
的基础上构造酉矩阵 ,即
,即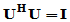
这由前面基扩充定理可知是可行的,从而有
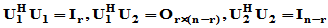
故
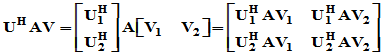
其中已知
 而
而 
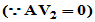
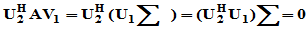
故定理得证。
奇异值分解的求法可按证明步骤求之。
作业: P225 1(2), 2, 5




