第九讲 矩阵微分方程
一、矩阵的微分和积分
1. 矩阵导数定义：若矩阵
的每一个元素
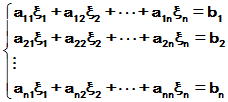是变量t的可微函数，则称A(t)可微，其导数定义为
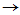
由此出发，函数可以定义高阶导数，类似地，又可以定义偏导数。
- 矩阵导数性质：若A(t),B(t)是两个可进行相应运算的可微矩阵，则
（1）
（2）
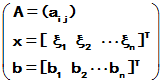
（3）
（4）
(A与t无关)
此处仅对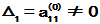
加以证明
证：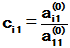
又
- 矩阵积分定义：若矩阵
的每个元素
都是区间
上的可积函数，则称A(t)在区间
上可积，并定义A(t)在
上的积分为
- 矩阵积分性质
（1）
（2）
（3）
- 阶线性齐次常系数常微分方程组
设有一阶线性其次常系数常微分方程组
式中t是自变量，
是t的一元函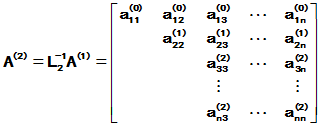数
是常系数。
令
，
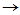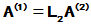
则原方程组变成如下矩阵方程
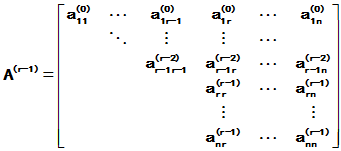
其解为
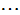
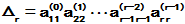
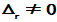
对该解求导，可以验证
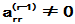且t＝0时，
表明x(t)确为方程的解，积分常数亦正确
例：求解微分方程组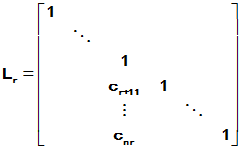
， 初始条件为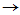
解：
，
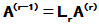
求出A的特征多项式，
， 
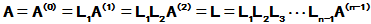
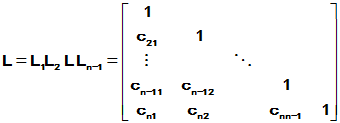定义待定系数的多项式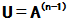 
解方程 
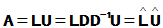
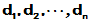
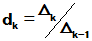
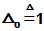
- 一阶线性非齐次常系数常微分方程组
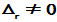
令
方程组化为矩阵方程
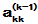
采用常数变易法求解之；齐次方程的解为
，可设非齐次方程的解为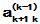
，
代入方程，得：
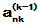
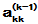
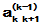
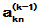
由积分性质(3)可验证c(t)是解。
加上初始条件
，有
说明:高阶常微分方程常常可以化为一阶常微分方程组来处理，
如：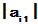 
令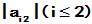
，则可得
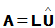
一般地，n阶常微分方程可以化为n个一阶常微分方程组成的方程组。
作业：p170-171 5、9
p177 3、4
