第六讲 Jordon 标准形的变换与应用
- Jordon标准形变换矩阵的求法
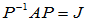
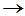
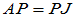
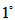 将P按J的结构写成列块的形式
将P按J的结构写成列块的形式



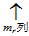
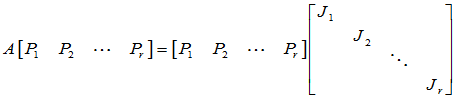
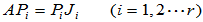
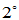 求解r个矩阵方程
求解r个矩阵方程 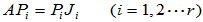
 将r个
将r个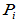 合成变换矩阵
合成变换矩阵 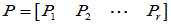
★ 关于方程
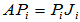 的求解
的求解

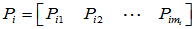

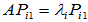
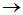
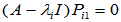

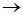
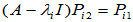
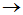
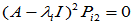
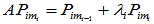
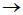
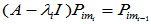

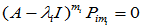
两种具体做法: (ⅰ) 按照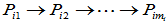 的顺序求解,即先求出特征向量
的顺序求解,即先求出特征向量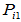 ,然后由后续方程求出
,然后由后续方程求出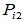 、
、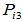 、…;(ⅱ)先求
、…;(ⅱ)先求 的特征向量
的特征向量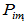 ,然后直接得到
,然后直接得到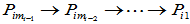 。
。
前一做法由于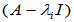 为奇异矩阵,每一步均存在多解及无解问题,故各步之间不能完全独立,前一步尚需依赖后一步、再后一步、…,直至最后一步才能完全确定一些待定系数;而后一做法仅出现一次求解方程,其余为直接赋值,无上述问题。但又可能导致低阶
为奇异矩阵,每一步均存在多解及无解问题,故各步之间不能完全独立,前一步尚需依赖后一步、再后一步、…,直至最后一步才能完全确定一些待定系数;而后一做法仅出现一次求解方程,其余为直接赋值,无上述问题。但又可能导致低阶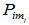 出现零向量的问题。
出现零向量的问题。
由于 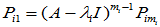
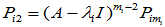

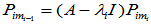
故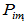 应满足:
应满足: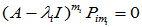 但
但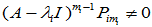
同一特征值可能出现在不同的Jordan块中,对于这种情况,按各Jordan块阶数高低一次进行处理,高阶先处理,低阶后处理,同阶同时处理。
- 最高阶(没有属于同一特征值的Jordan块同阶)可按下述方法求出
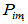 ,即使
,即使 但
但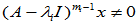 的
的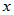 作为
作为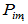 。
。
然后由方程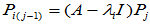 依次求出
依次求出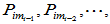 直至
直至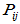 且j等于下一个属于同一特征值的Jordan块的阶数。
且j等于下一个属于同一特征值的Jordan块的阶数。
- 对于上述新Jordan块,它的
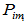 不仅要考虑到满足
不仅要考虑到满足
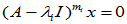 但
但 ,
,
而且还应与前述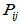 线性无关。
线性无关。
- 其它属于同一特征值的Jordan块处理时,按照(2)的原则处理即可。
- 出现多个属于同一特征值的Jordan块同阶时,还应考虑线性无关问题。
例:求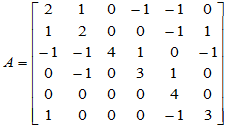 的Jordan标准形及其变换矩阵。
的Jordan标准形及其变换矩阵。
[解]:上一讲已求出其Jordan标准形,也可按如下方法求得。
(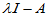 )可采用初等变换化为
)可采用初等变换化为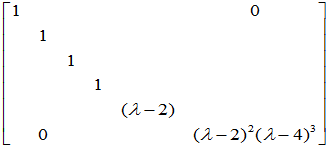
按此得出Jordon标准形
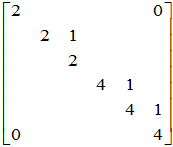
同时可见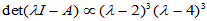 ,即
,即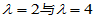 匀为三重特征值.
匀为三重特征值.
下面求变换矩阵P
(1) 的Jordon矩阵仅有一块,
的Jordon矩阵仅有一块,
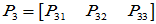
先求 ,
,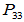 应满足
应满足 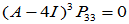
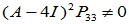
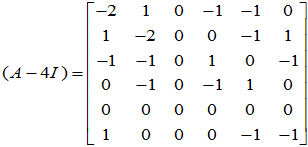
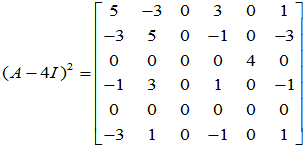
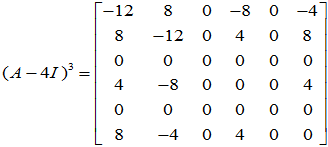
求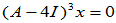
 设
设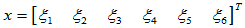
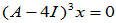 其通解为
其通解为
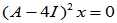 其通解为
其通解为
可取 =
=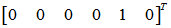

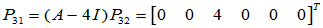
(2)对 存在两个Jordan块,
存在两个Jordan块,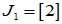 ,
, ,
,
分别对应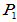 ,
,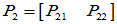
从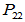 入手:
入手: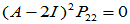 ,
,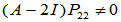
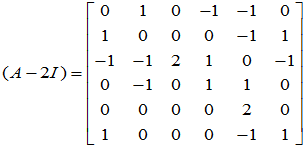
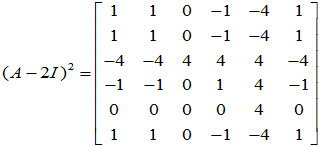
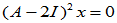
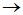

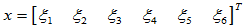 =
=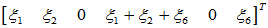
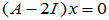
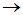
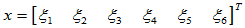 =
=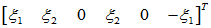
取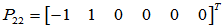
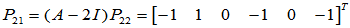
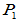 :
: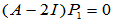
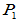 与
与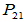 应线性无关,可取
应线性无关,可取 =
=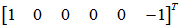
(3)合成变换矩阵
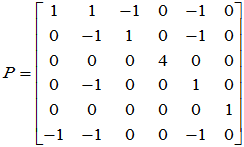
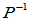 存在
存在
可以验证: 
二、 Jordan标准形的幂及多项式
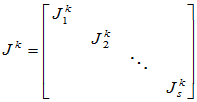 , 即
, 即 ,
,

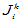 亦为类似的上三角形条带矩阵,在与主对角线平行的斜线上各元素相等. 其中
亦为类似的上三角形条带矩阵,在与主对角线平行的斜线上各元素相等. 其中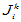 第一行的元素依次为
第一行的元素依次为

设有多项式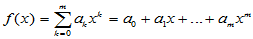 .则
.则

又 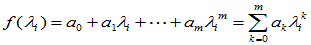
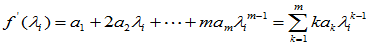
……
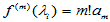
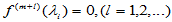
故
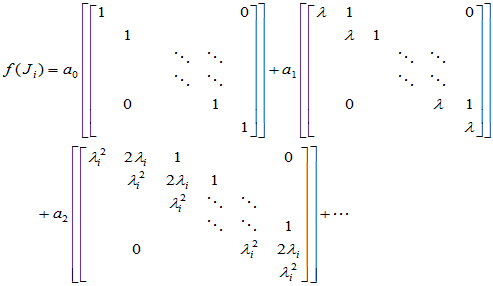
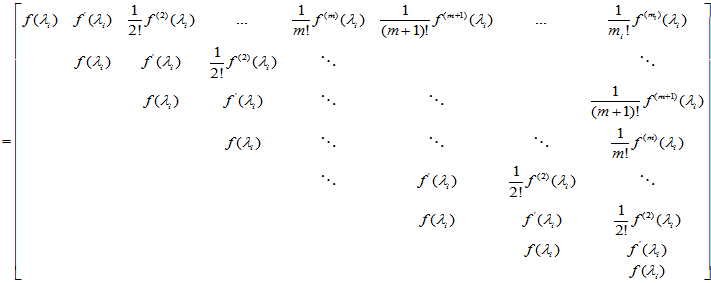
这就是说, 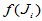 仍为上三角矩阵, 在与主对角线平行的斜线上各元素均相等, 而
仍为上三角矩阵, 在与主对角线平行的斜线上各元素均相等, 而
其第一行元素依次为
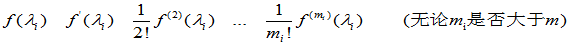
若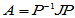 , 则
, 则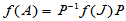 计算十分方便,无需再采用矩阵乘积.
计算十分方便,无需再采用矩阵乘积.
作业: P107 11




