第四讲 矩阵的对角化
 基
基
元素 | 坐标向量 | |
加法 | 元素加法 | 坐标向量的加法 |
数乘 | 数与元素"乘" | 数与坐标向量相乘 |
线性变换及其作用 | 对应关系 | 矩阵与坐标列向量的乘积 |
对任何线性空间,给定基后,我们对元素进行线性变换或线性运算时,只需用元素的坐标向量以及线性变换的矩阵即可,因此,在后面的内容中着重研究矩阵和向量。

对角矩阵的形式比较简单,处理起来较方便,比如求解矩阵方程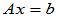 时,将矩阵
时,将矩阵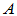 对角化后很容易得到方程的解。对角化的过程实际上是一个去耦的过程。以前我们学习过相似变化对角化。那么,一个方阵是否总可以通过相似变化将其对角化呢?或者对角化需要什么样的条件呢?如果不能对角化,我们还可以做哪些处理使问题变得简单呢?
对角化后很容易得到方程的解。对角化的过程实际上是一个去耦的过程。以前我们学习过相似变化对角化。那么,一个方阵是否总可以通过相似变化将其对角化呢?或者对角化需要什么样的条件呢?如果不能对角化,我们还可以做哪些处理使问题变得简单呢?
- 特征征值与特征向量
1. 定义:对 阶方阵
阶方阵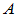 ,若存在数
,若存在数 ,及非零向量(列向量)
,及非零向量(列向量)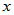 ,使得
,使得 ,则称
,则称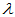 为
为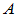 的特征值,
的特征值,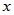 为
为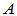 的属于特征值
的属于特征值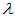 的特征向量。
的特征向量。
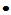 特征值不唯一
特征值不唯一
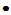 特征向量非零
特征向量非零
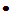
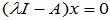 有非零解,则
有非零解,则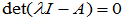 ,称
,称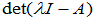 为
为 的多项式。
的多项式。
[例1]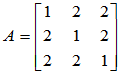 ,求其特征值和特征向量。
,求其特征值和特征向量。
[解] 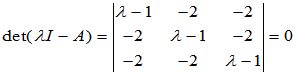
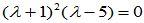
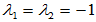
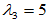
属于特征值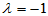 的特征向量
的特征向量 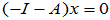
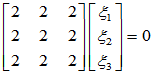
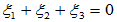
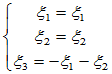
可取基础解系为 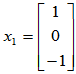
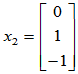
属于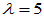 的特征向量
的特征向量 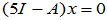
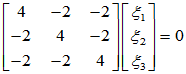
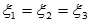
可取基础解系为 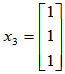
2. 矩阵的迹与行列式
 所有对角元素之和
所有对角元素之和

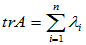
3. 两个定理
- 设
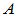 、
、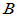 分别为
分别为 和
和 阶矩阵,则
阶矩阵,则
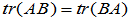
(2)sylvster定理:设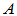 、
、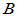 分别为
分别为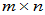 和
和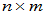 阶矩阵,则
阶矩阵,则
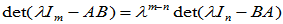
即:AB与BA的特征值只差零特征值的个数,非零特征值相同。
- 矩阵对角化的充要条件
定理:
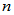 阶方阵
阶方阵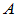 可通过相似变换对角化的充要条件是它具有
可通过相似变换对角化的充要条件是它具有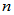 个线性无关的特征向量。
个线性无关的特征向量。
[证明] 充分性:已知
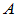 具有
具有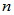 个线性无关的特征向量
个线性无关的特征向量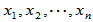 ,则
,则
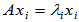
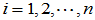
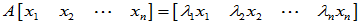
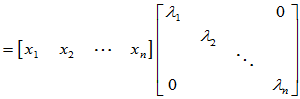
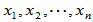 线性无关,故
线性无关,故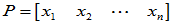 为满秩矩阵,
为满秩矩阵,
令
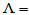
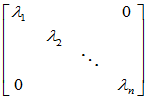 ,则有
,则有
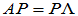

必要性:已知存在可逆方阵
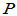 ,使
,使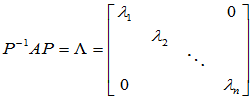
将
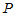 写成列向量
写成列向量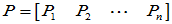 ,
,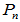 为
为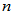 维列向量
维列向量
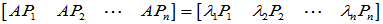
可见,
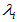 为
为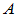 的特征值,
的特征值, 为
为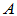 的特征向量,
的特征向量,
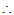
 具有
具有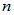 个线性无关的特征向量。
个线性无关的特征向量。
推论:
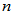 阶方阵有
阶方阵有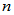 个互异的特征值,则必可对角化。(充分条件)
个互异的特征值,则必可对角化。(充分条件)
- 内积空间
1. Euclid空间
设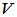 是实线性空间(
是实线性空间(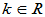 ),对于
),对于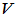 中任何两个元素
中任何两个元素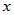 、
、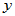 均按某一规则存在一个实数与之对应,记为
均按某一规则存在一个实数与之对应,记为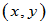 ,若它满足
,若它满足
(1)交换律 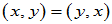
(2)分配律 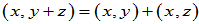
(3)齐次律 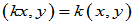
(4)非负性  ,当且仅当
,当且仅当 时,
时,
则称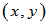 为
为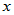 与
与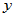 的内积,定义了内积的实线性空间称为Euclid空间。
的内积,定义了内积的实线性空间称为Euclid空间。
对于一个给定的线性空间,可以定义多种内积,较典型的如三维向量空间的数量积就满足以上四条性质,构成内积。以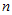 维向量空间为例:
维向量空间为例:
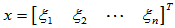 ,
,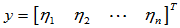
可定义内积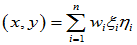
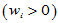 ,它满足内积的四条性质:
,它满足内积的四条性质:
(1)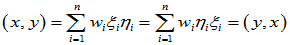
(2)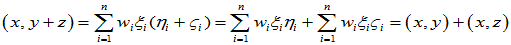
(3)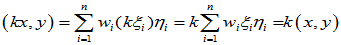
(4)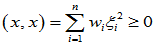 当且仅当
当且仅当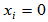 时,
时,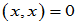
该内积可写为: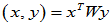 ,其中
,其中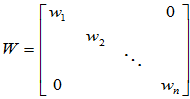
更一般的,对实对称正定矩阵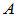 ,
,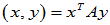 也满足内积的定义。
也满足内积的定义。
正定:(1)特征值全为正(2)各阶顺序主子式大于0
2. 酉空间:
设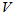 是复线性空间(
是复线性空间(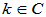 ),对于
),对于 中任何两个元素
中任何两个元素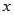 、
、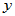 均按某一规则存在一个复数与之对应,记为
均按某一规则存在一个复数与之对应,记为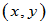 ,若它满足
,若它满足
(1)交换律 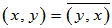
(2)分配律 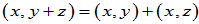
(3)齐次律  or
or 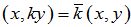
(4)非负性  ,当且仅当
,当且仅当 时,
时,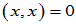
则称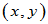 为
为 与
与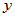 的内积,定义了内积的复线性空间称为酉空间。
的内积,定义了内积的复线性空间称为酉空间。
以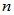 维向量空间为例,
维向量空间为例,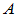 为厄米(
为厄米( )正定(
)正定(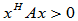 )矩阵,
)矩阵,

较常见的比如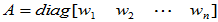 ,
,
最简单:实 
复 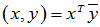
3. 正交性:若 ,则称
,则称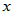 与
与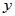 正交。
正交。
 与
与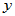 的夹角:
的夹角: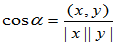 ,
,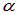 称为
称为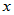 与
与 的夹角。
的夹角。
4. Gram-Schmidt正交化手续
设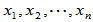 为一组线性无关的元素或向量,可以进行如下正交归一化操作(正交规范化或正交单位化):
为一组线性无关的元素或向量,可以进行如下正交归一化操作(正交规范化或正交单位化):
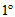
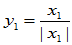
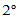
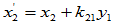 选择合适的
选择合适的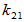 使
使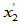 与
与 正交,
正交,
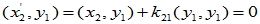
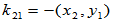

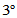
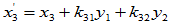 选择
选择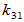 、
、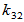 使
使 与
与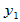 和
和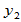 均正交
均正交
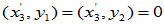
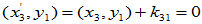

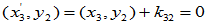
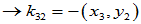
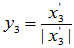
一般的,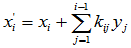
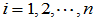
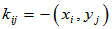
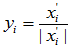
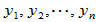 成为一组正交归一化向量:
成为一组正交归一化向量:
若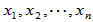 为一组基元素,则
为一组基元素,则 成为标准正交基。
成为标准正交基。
作业:P106-107 1(1)(2),2,4,5,10,11




