第二讲 线性子空间
一、线性子空间的定义及其性质
- 定义:设V1是数域K上的线性空间V的一个非空子集合,且对V已有的线性运算满足以下条件
- 如果x、y
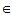 V1,则x+y
V1,则x+y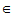 V1;
V1;
- 如果x
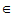 V1,k
V1,k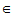 K,则kx
K,则kx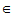 V1,
V1,
则称V1是V的一个线性子空间或子空间。
- 性质:(1)线性子空间V1与线性空间V享有共同的零元素;
(2)V1中元素的负元素仍在V1中。
[证明](1) 0
0
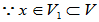
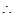 V中的零元素也在V1中,V1与V享有共同的零元素。
V中的零元素也在V1中,V1与V享有共同的零元素。
(2)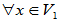
(-1)x=(-x)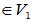 封闭性
封闭性
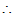 V1中元素的负元素仍在V1中
V1中元素的负元素仍在V1中
- 分类:子空间可分为平凡子空间和非平凡子空间
平凡子空间:{0}和V本身
非平凡子空间:除以上两类子空间
4. 生成子空间:设x1、x2、···、xm为V中的元素,它们的所有线性组合的集合
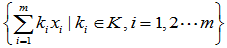
也是V的线性子空间,称为由x1、x2、···、xm生(张)成的子空间,记为L(x1、x2、···、xm)或者Span(x1、x2、···、xm)。
若x1、x2、···、xm线性无关,则
dim{L(x1、x2、···、xm)}=m
5. 基扩定理:设V1是数域K上的线性空间Vn的一个m维子空间,x1、x2、···、xm是V1的一个基,则这m个基向量必可扩充为Vn的一个基;换言之,在Vn中必可找到n-m个元素xm+1、xm+2、···、xn,使得x1、x2、···、xn成为Vn的一个基。这n-m个元素必不在V1中。
二、子空间的交与和
1.定义:设V1、V2是线性空间V的两个子空间,则
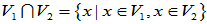
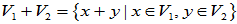
分别称为V1和V2的交与和。
2.定理:若V1和V2是线性空间V的两个子空间,则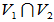 ,V1+V2均为V的子空间
,V1+V2均为V的子空间
[证明](1)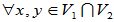
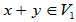

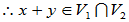
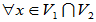
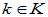
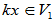
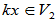
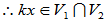
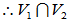 是V的一个线性子空间。
是V的一个线性子空间。
(2)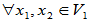
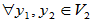

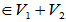
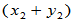





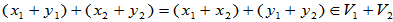
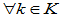
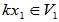
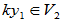
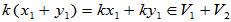
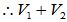 是V的子空间。
是V的子空间。
- 维数公式:若V1、V2是线性空间V的子空间,则有
dim(V1+V2)+ dim(V1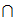 V2)= dimV1+ dimV2
V2)= dimV1+ dimV2
[证明] 设dimV1=n1, dimV2=n2, dim(V1 V2)=m
V2)=m
需要证明dim(V1+V2)=n1+n2-m
设x1、x2、···、xm是V1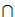 V2的一个基,根据基扩定理
V2的一个基,根据基扩定理
存在1)y1、y2、···、yn1-m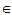 V1,使x1、x2、···、xm、y1、y2、···、yn1-m成为V1的一个基;
V1,使x1、x2、···、xm、y1、y2、···、yn1-m成为V1的一个基;
2)z1、z2、···、zn2-m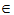 V2,使x1、x2、···、xm、z1、z2、···、zn2-m
V2,使x1、x2、···、xm、z1、z2、···、zn2-m
成为V2的一个基;
考察x1、x2、···、xm、y1、y2、···、yn1-m、z1、z2、···、zn2-m,
若能证明它为V1+V2的一个基,则有dim(V1+V2)=n1+n2-m。
成为基的两个条件:
- 它可以线性表示V1+V2中的任意元素
- 线性无关
显然条件1)是满足的,现在证明条件2),采用反证法。
假定上述元素组线性相关,则存在一组不全为0的数k1、k2、···、km、p1、p2、···、pn1-m、q1、q2、···、qn2-m使
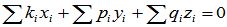
令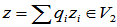 ,则
,则
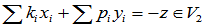 但
但
根据基扩定理 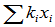

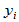
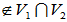 , x1、x2、···、xm、y1、y2、···、yn1-m成为V1的一个基
, x1、x2、···、xm、y1、y2、···、yn1-m成为V1的一个基
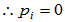
同理:
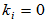
这与假设矛盾,所以上述元素线性无关,可作为V1+V2的一个基。
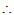 dim(V1+V2)=n1+n2-m
dim(V1+V2)=n1+n2-m
三、子空间的直和
1. 定义:设V1、V2是线性空间V的子空间,若其和空间V1+V2中的任一元素只能唯一的表示为V1的一个元素与V2的一个元素之和,即 ,存在唯一的
,存在唯一的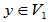 、
、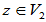 ,使
,使 ,则称
,则称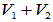 为V1与V2的直和,记为
为V1与V2的直和,记为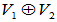
子空间的直和并不是一种特殊的和,仍然是
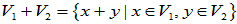 ,
,
反映的是两个子空间的关系特殊。
2. 定理:如下四种表述等价
(1)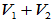 成为直和
成为直和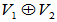
(2)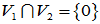
(3)dim(V1+V2)=dimV1+ dimV2
(4)x1、x2、···、xs为V1的基,y1、y2、···、yt为V2的基,则x1、x2、···、xs、y1、y2、···、yt为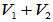 的基
的基
[证明](2)和(3)的等价性显然
采用循环证法:(1)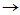 (2)
(2)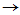 (4)
(4)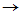 (1)
(1)
(1) (2):已知
(2):已知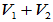 =
=
假定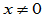 且
且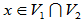 ,则
,则
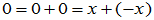
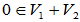 ,
,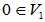 ,
,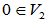 ,
,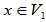 ,
,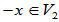
说明对0元素存在两种分解,这与直和的定义矛盾,所以假定不成立,在 中只能存在0元素,即
中只能存在0元素,即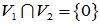
(2)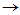 (4):已知
(4):已知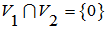
成为基的两个条件:
- 可以线性表示V1+V2中的任意元素
2)线性无关
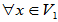 、
、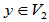 ,存在如下坐标表示式
,存在如下坐标表示式
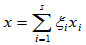
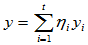
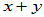 可表示V1+V2中的任一元素,
可表示V1+V2中的任一元素,
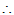 x1、x2、···、xs、y1、y2、···、yt可表示V1+V2中的任意元素。
x1、x2、···、xs、y1、y2、···、yt可表示V1+V2中的任意元素。
假设x1、x2、···、xs、y1、y2、···、yt线性相关,即存在不全为0的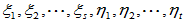 使
使
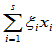
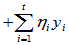 =0
=0
而 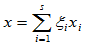
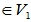
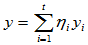
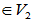
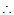
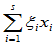 =-y
=-y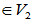

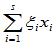

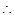
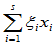 =0
=0
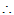
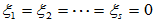
同理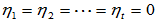
这与其线性相关性矛盾,x1、x2、···、xs、y1、y2、···、yt线性无关
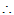 x1、x2、···、xs、y1、y2、···、yt可作为
x1、x2、···、xs、y1、y2、···、yt可作为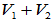 的基
的基
(4)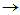 (1):已知(4)成立
(1):已知(4)成立
在x1、x2、···、xs、y1、y2、···、yt这组基下
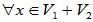 存在唯一的坐标
存在唯一的坐标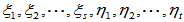 使
使
x=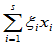

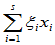
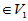

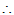
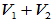 成为直和
成为直和
作业:P25-26,11、12、13




 浙公网安备 33010602011771号
浙公网安备 33010602011771号