前言:为什么要学习矩阵理论?怎么来学习、掌握?
- 向量、矩阵及其运算法则是描述、分析、处理线性系统的有力工具——其"有力"具体表现在这种工具的普适性和简便性上。
- 学习基础知识
 专业课程中进一步认知
专业课程中进一步认知  科学研究中应用
科学研究中应用
第一讲 线性空间
一、线性空间的定义及性质
[预备知识]
★ 集合:笼统地说是指一些事物(或者对象,称为元素)组成的整体。
集合的表示:枚举、表达式,如
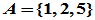 ;
; 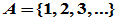 ;
; 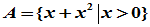
集合的运算:并(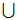 ),交(
),交(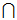 )
)
另外,集合的"和"( ):并不是严格意义上集合的运算,因为它限定了集合中元素须有可加性。
):并不是严格意义上集合的运算,因为它限定了集合中元素须有可加性。
★ 数域:一种数集,对四则运算封闭(除数不为零)。比如有理数域、实数域(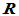 )和复数域(
)和复数域( )。实数域和复数域是工程上较常用的两个数域。
)。实数域和复数域是工程上较常用的两个数域。
线性空间是线性代数最基本的概念之一,也是学习矩阵理论的重要基础。线性空间的概念是对各种具体线性系统的一种统一的抽象。
1. 线性空间的定义:
设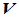 是一个非空集合,其元素用
是一个非空集合,其元素用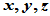 等表示;
等表示;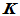 是一个数域,其元素用
是一个数域,其元素用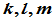 等表示。如果
等表示。如果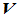 满足
满足
(I)在 中定义一个"加法"运算,即当
中定义一个"加法"运算,即当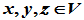 时,有唯一的"和"
时,有唯一的"和"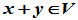 (封闭性),且加法运算满足下列性质
(封闭性),且加法运算满足下列性质
(1)结合律 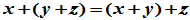 ;
;
(2)交换律 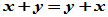 ;
;
(3)零元律 存在零元素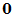 ,使
,使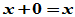 ;
;
(4)负元律 对于任一元素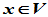 ,存在一元素
,存在一元素 ,使
,使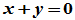 ,且称
,且称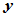 为
为 的负元素,记为
的负元素,记为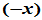 。即,
。即,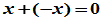 。
。
(II)在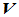 中定义一个"数乘"运算,即当
中定义一个"数乘"运算,即当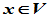 ,
,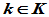 时,有唯一的"积"
时,有唯一的"积" (封闭性),且数乘运算满足下列性质
(封闭性),且数乘运算满足下列性质
(5)数因子分配律 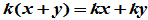 ;
;
(6)分配律 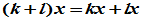 ;
;
(7)结合律 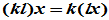 ;
;
(8)恒等律 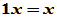 ;
;
则称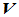 为数域
为数域 上的线性空间。
上的线性空间。
注意:
(1)线性空间不能离开某一数域来定义。实际上,对于不同数域,同一个集合构成的线性空间会不同,甚至一种能成为线性空间而另一种不能成为线性空间。
(2)两种运算、八条性质
数域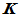 中的运算是具体的四则运算,而
中的运算是具体的四则运算,而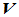 中所定义的加法运算和数乘运算则可以十分抽象。
中所定义的加法运算和数乘运算则可以十分抽象。
(3)除了两种运算和八条性质外,还应注意唯一性、封闭性
唯一性一般较显然,封闭性还需要证明,出现不封闭的情况:集合小、运算本身就不满足。
当数域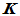 为实数域时,
为实数域时,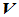 就称为实线性空间;
就称为实线性空间;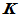 为复数域,
为复数域,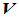 就称为复线性空间。
就称为复线性空间。
例1. 设 ={全体正实数},其"加法"及"数乘"运算定义为
={全体正实数},其"加法"及"数乘"运算定义为
x y=xy ,
y=xy , 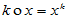
证明: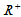 是实数域R上的线性空间。
是实数域R上的线性空间。
证:首先需要证明两种运算的唯一性和封闭性
①唯一性和封闭性
 唯一性显然
唯一性显然
 若x>0,y>0,
若x>0,y>0, 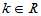 ,则有
,则有
 x
x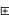 y=xy
y=xy
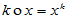
 封闭性得证。
封闭性得证。
②八条性质
(1) x
x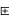 (y
(y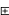 z)=x(yz)=(xy)z=(x
z)=x(yz)=(xy)z=(x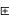 y)
y)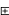 z
z
(2) x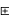 y=xy=yx= y
y=xy=yx= y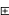 x
x
(3) 1是零元素 x 1=
1=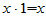 [x
[x o=x——>xo=x->o=1]
o=x——>xo=x->o=1]
(4) 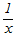 是x的负元素 x
是x的负元素 x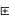
 =
= [x+y=o ]
[x+y=o ]
(5) 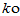 (x
(x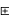 y)
y)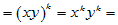
 x
x
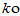 y [数因子分配律]
y [数因子分配律]
(6) 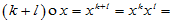 (
(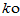 x)
x)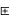 (
(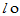 x) [分配律]
x) [分配律]
(7)  [结合律]
[结合律]
(8) 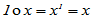 [恒等律]
[恒等律]
由此可证,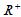 是实数域R上的线性空间。
是实数域R上的线性空间。
- 定理:线性空间具有如下性质
- 零元素是唯一的,任一元素的负元素也是唯一的。
- 如下恒等式成立:
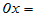 o,
o, 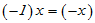 。
。
证明:(1)采用反证法:
①零元素是唯一的。 设存在两个零元素o1和o2,则由于o1和o2 均为零元素, 按零元律有 [交换律]
o1+o2=o1 = o2+o1=o2
所以 o1=o2
即 o1和o2 相同,与假设相矛盾,故只有一个零元素。
②任一元素的负元素也是唯一的。假设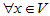 ,存在两个负元素
,存在两个负元素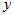 和
和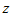 ,则根据负元律有
,则根据负元律有
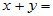 o=
o=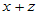
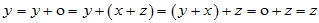
[零元律] [结合律] [零元律]
即 和
和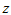 相同,故负元素唯一。
相同,故负元素唯一。
(2) ①:设w=0x,则 x+w=1x+0x=(1+0)x=x,故 w=o。
[恒等律]
②:设w=(-1)x,则x+w=1x+(-1)x=[1+(-1)]x=0x=o,故w=-x。
- 线性相关性
线性空间中相关性概念与线性代数中向量组线性相关性概念类似。
•线性组合: 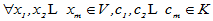
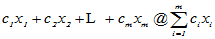
称为元素组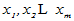 的一个线性组合。
的一个线性组合。
•线性表示: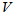 中某个元素x可表示为其中某个元素组的线性组合,则称x可由该元素组线性表示。
中某个元素x可表示为其中某个元素组的线性组合,则称x可由该元素组线性表示。
•线性相关性:如果存在一组不全为零的数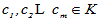 ,使得对于元素
,使得对于元素 有
有
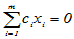
则称元素组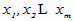 线性相关,否则称其线性无关。【线性相关性概念是个非常重要的概念,有了线性相关性才有下面的线性空间的维数、基和坐标】
线性相关,否则称其线性无关。【线性相关性概念是个非常重要的概念,有了线性相关性才有下面的线性空间的维数、基和坐标】
- 线性空间的维数
定义:线性空间 中最大线性无关元素组所含元素个数称为
中最大线性无关元素组所含元素个数称为 的维数,记为
的维数,记为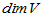 。
。
本课程只考虑有限维情况,对于无限维情况不涉及 。
例2. 全体m×n阶实矩阵的集合构成一个实线性空间(对于矩阵加法和数对矩阵的数乘运算),求其维数。
解:一个直接的方法就是找一个最大线性无关组,其元素尽可能简单。
令Eij为这样的一个m×n阶矩阵,其(i, j)元素为1,其余元素为零。
显然,这样的矩阵共有mn个,构成一个具有mn个元素的线性无关元素组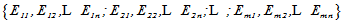 。另一方面,还需说明元素个数最大。对于任意的
。另一方面,还需说明元素个数最大。对于任意的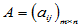 ,都可由以上元素组线性表示,
,都可由以上元素组线性表示,
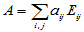 ——>
——> 
即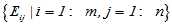 构成了最大线性无关元素组,所以该空间的维数为mn。
构成了最大线性无关元素组,所以该空间的维数为mn。
- 线性空间的基与坐标
- 基的定义:设V是数域K上的线性空间,
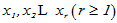 是属于V的r个任意元素,如果它满足
是属于V的r个任意元素,如果它满足
(1)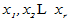 线性无关;
线性无关;
(2)V中任一向量x均可由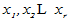 线性表示。
线性表示。
则称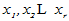 为V的一个基,并称
为V的一个基,并称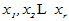 为该基的基元素。
为该基的基元素。
•基正是V中最大线性无关元素组;V的维数正是基中所含元素的个数。
•基是不唯一的,但不同的基所含元素个数相等。
- 考虑全体复数所形成的集合C。如果K=C(复数域),则该集合对复数加法和复数复数的乘法构成线性空间,其基可取为1,空间维数为1;如果取K=R(实数域),则该集合对复数加法及实数对复数的数乘构成线性空间,其基可取为{1,i},空间维数为2。
数域K | 两种运算 | 基 | 一般元素 | 空间类型 | 维数 |
复数域C | (1)复数加法;(2)复数对复数的数乘 | {1} |
| 复线性空间 | 1 |
实数域R | (1)复数加法;(2)实数对复数的数乘 | {1,i} |
| 实线性空间 | 2 |
- 坐标的定义:称线性空间
 的一个基
的一个基 为
为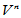 的一个坐标系,
的一个坐标系,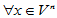 ,它在该基下的线性表示为:
,它在该基下的线性表示为:
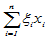
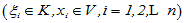
则称 为x在该坐标系中的坐标或分量,记为
为x在该坐标系中的坐标或分量,记为 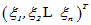
讨论:(1)一般来说,线性空间及其元素是抽象的对象,不同空间的元素完全可以具有千差万别的类别及性质。但坐标表示却把它们统一了起来,坐标表示把这种差别留给了基和基元素,由坐标所组成的新向量仅由数域中的数表示出来。
(2)更进一步,原本抽象的"加法"及 "数乘"经过坐标表示就演化为向量加法及数对向量的数乘。
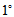
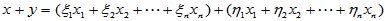
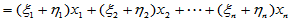

正对应 

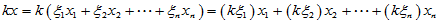
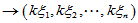
正对应 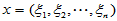
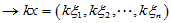
(3)显然,同一元素在不同坐标系中的坐标是不同的。后面我们还要研究这一变换关系。
- 基变换与坐标变换
基是不唯一的,因此,需要研究基改变时坐标变换的规律。
设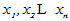 是
是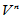 的旧基,
的旧基,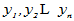 是
是 的新基,由于两者都是基,所以可以相互线性表示
的新基,由于两者都是基,所以可以相互线性表示
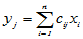 (
(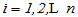 )
)
即 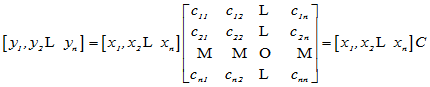
其中C称为过渡矩阵,上式就给出了基变换关系,可以证明,C是可逆的。
设 ,它在旧基下的线性表示为
,它在旧基下的线性表示为
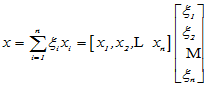
它在新基下的线性表示为

则 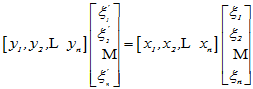
由于基元素的线性无关性,得到坐标变换关系

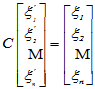

作业:P25-26 3,5,7,9
补充:证明对于线性空间的零元素o,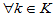 ,均有ko=o。
,均有ko=o。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号