§3 二次曲线的切线和奇点
一 切线:
1、定义:若一直线l与二次曲线C交于二重合实点,或l整个在二次曲线C上,则称l
为C的切线。切线与C的公共点称为切点。
2、求法:
设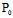 (
(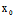 ,
, )∈C,以
)∈C,以 为切点的切线 l:
为切点的切线 l: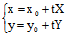
今确定X:Y
1°当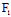 (
(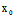 ,
,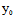 ),
), (
(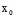 ,
,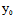 )不全为0时,
)不全为0时,
若X:Y不是渐近方向,则l与C相切〈═〉l与C交于二重合实点
〈═〉△=[ (
(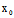 ,
, )X+
)X+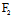 (
( ,
, )Y]²-Φ(X,Y)F(
)Y]²-Φ(X,Y)F(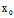 ,
,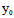 )=0
)=0
〈═〉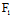 (
(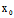 ,
,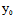 )X+
)X+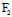 (
(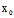 ,
, )Y=0〈═〉X:Y=-
)Y=0〈═〉X:Y=-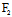 (
(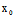 ,
,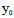 ):
):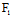 (
( ,
,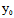 )
)
若X:Y是渐近方向,则l与C相切〈═〉l处在C上〈═〉
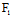 (
(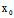 ,
,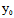 )X+
)X+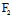 (
(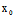 ,
,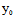 )Y=0〈═〉X:Y=-
)Y=0〈═〉X:Y=-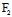 (
( ,
, ):
):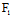 (
( ,
, )
)
从而切线l:
即 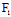 (
(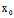 ,
, )(x-
)(x- )+
)+ (
(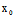 ,
,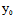 )(y-
)(y-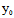 )=0
)=0
 (
(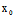 ,
,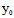 )x+
)x+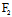 (
(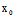 ,
, )y-[
)y-[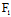 (
(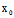 ,
,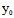 )
)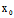 +
+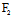 (
(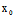 ,
, )
) ]=0
]=0
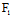 (
(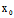 ,
, )x+
)x+ (
(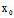 ,
,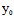 )y+
)y+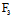 (
( ,
, )=0
)=0
亦即
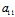
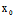 x+
x+ (
(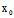 y+
y+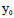 x)+
x)+
 y+
y+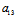 (x+
(x+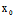 )+
)+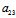 (y+
(y+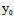 )+
)+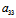 =0 (*)
=0 (*)
注:在 (
( ,
,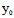 )与
)与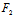 (
(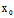 ,
,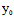 )不全为0时,(*)即为以
)不全为0时,(*)即为以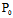 (
(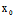 ,
,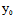 )为切点的切线方程。不难看出,若
)为切点的切线方程。不难看出,若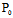 (
(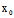 ,
,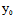 )使
)使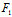 (
(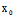 ,
,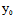 ),
),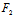 (
(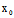 ,
, )不全为0,则要求以
)不全为0,则要求以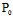 为切点的切线,只需要在C的方程中,以
为切点的切线,只需要在C的方程中,以
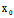 x ,
x ,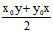 ,
, y ,
y ,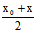 ,
,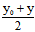
替换x² xy y² x y
即可
2°当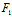 (
(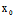 ,
, )=
)=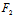 (
( ,
, )=0时,
)=0时,
对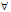 过
过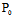 且沿非渐近方向的直线l:
且沿非渐近方向的直线l: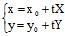 ,
,
△=[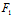 (
(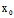 ,
,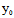 )X+
)X+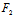 (
(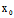 ,
,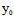 )Y]²-Φ(X,Y)F(
)Y]²-Φ(X,Y)F(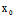 ,
,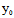 )=0
)=0
∴l是切线;而对任意过 且沿渐近方向的直线l:
且沿渐近方向的直线l: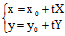
Φ(X,Y)= (
(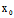 ,
,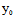 )X+
)X+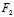 (
(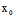 ,
,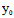 )Y=F(
)Y=F(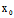 ,
,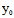 )=0,
)=0,
∴l整个在曲线 即l也是切线
可见,若曲线C上一点 (
(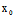 ,
,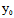 )使
)使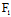 (
(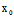 ,y。)=
,y。)=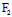 (
(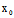 ,
,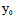 )=0,则过
)=0,则过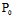 的任一直线均是C的切线。为使得过C上任一点只有唯一切线,在这种情形下,通常只取过
的任一直线均是C的切线。为使得过C上任一点只有唯一切线,在这种情形下,通常只取过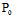 且沿渐近方向的直线作为C的切线。
且沿渐近方向的直线作为C的切线。
二 奇点:
1、定义:二次曲线上坐标满足 的点称为奇点。二次曲线上的非奇点又称为正常点。
的点称为奇点。二次曲线上的非奇点又称为正常点。
可见:
1°一点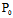 (
(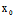 ,
,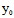 )为奇点〈═〉
)为奇点〈═〉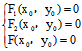 〈═〉
〈═〉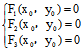
2°奇点必是中心,但中心未必是奇点,从而无心曲线没有奇点。
3°在奇点处,曲线有沿渐近方向的切线;而在正常点处,曲线有沿
X:Y=-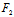 (
(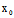 ,
,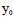 ):
):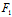 (
(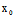 ,
,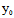 )的切线,从而在正常点处,切线是唯一的
)的切线,从而在正常点处,切线是唯一的
2、性质:
1°二次曲线有奇点的必要条件是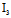 =0
=0
事实上,若二次曲线有奇点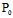 (
(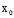 ,
,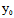 ),则
),则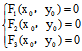
∴方程组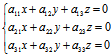 有非0解(
有非0解(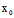 ,
,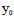 ,1)
,1)
∴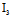 =0
=0
思考: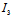 =0是否为二次曲线有奇点的充分条件?为什么?
=0是否为二次曲线有奇点的充分条件?为什么?
2°二次曲线有奇点的充要条件是其为有心二次曲线,其中心全在二次曲线上,
事实上"〈═"显然
"═〉"设二次曲线F(x,y)=0有奇点。
若曲线为中心二次曲线,则这唯一中心也是奇点
∴中心在曲线上;
若曲线为线心曲线,因它有奇点 ∴方程组

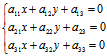 有解
有解

 同解
同解
同解
 有解
有解
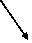 而
而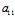 :
: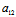 =
= :
: ∴
∴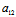 :
: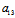 =
=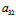 :
:
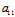 :
: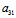 =
= :
: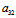 =
= :
: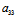
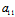 x+
x+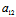 y+
y+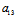 =0
=0
∴中心全是奇点,从而所有中心都在曲线上。
例:求二次曲线y²-4x-4y=0的切线l
(i)l过点(3,-2);
(ii)l过点(-1,0)。
解:(i)易验证点(3,-2)在曲线上,且该曲线上无奇点,∴切线方程为
-2y-2(y-2)-2(x+3)=0
即 x+2y+1=0
(ii)易验证(-1,0)不在曲线上,
法一:设过(-1,0)的切线l与曲线切于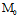 (
(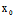 ,
,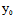 )
)
则 l:y -2(y+
-2(y+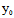 )-2(x+
)-2(x+ )=0
)=0
而(-1,0)∈l ∴-2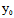 -2(
-2( -1)=0
-1)=0
即  +
+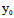 -1=0
-1=0
又 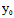 ²-4
²-4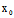 -4
-4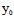 =0
=0
∴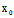 =-1,3
=-1,3 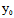 =2,-2 ∴切线l:2y-2(y+2)-2(x-1)=0
=2,-2 ∴切线l:2y-2(y+2)-2(x-1)=0
或-2y-2(y-2)-2(x+3)=0 即
x+1=0或x+2y+1=0
法二:
设过(-1,0)饿切线l: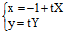 则
则
△=[ (-1,0)X+
(-1,0)X+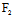 (-1,0)Y]²-Φ(X,Y)F(-1,0)=0
(-1,0)Y]²-Φ(X,Y)F(-1,0)=0
即 [-2X-2Y]²-4Y²=0
亦即X²+2XY=0 ∴X=0或X=-2Y
∴X:Y=0:1 或 X:Y=-2:1 ∴ l: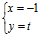 或 l:
或 l:
法三:设切线l: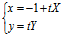 则 X:Y =(x+1):y
则 X:Y =(x+1):y
而△=[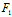 (-1,0)X+
(-1,0)X+ (-1,1)Y]²-Φ(X,Y)F(-1,0)=0
(-1,1)Y]²-Φ(X,Y)F(-1,0)=0
∴[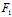 (-1,0)(x+1)+
(-1,0)(x+1)+ (-1,0)y]²-4y²=0
(-1,0)y]²-4y²=0
即[-1(x+1)-2y]²-4y²=0
亦即(x+y+1)²-y²=0 ∴x+1=0或 x+2y+1=0
三 二次曲线的法线:
定义:设二次曲线F(x,y)=0在 处存在切线,称过
处存在切线,称过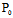 且垂直于切线的直线为曲
且垂直于切线的直线为曲
线在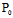 的法线。
的法线。
求法:若 (
(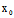 ,
,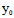 )是二次曲线F(x,y)上的正常点,则
)是二次曲线F(x,y)上的正常点,则
法线 l:




