§5 二次曲线的主直径
一 定义:
设X:Y为二次曲线F(x,y)=0的一非渐近方向,若共轭于该方向的直径:
X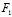 (x,y)+Y
(x,y)+Y (x,y)=0 (1)
(x,y)=0 (1)
与方向X:Y垂直,则称这直径为二次曲线的主直径;而直径(1)的方向及方向X:Y均称为二次曲线的主方向。
注:1°主直径事实上是二次曲线的对称轴,简称为二次曲线的轴,轴与曲线的交点称为曲线的顶点。
2°可以证明:一方向X:Y为主方向〈═〉X:Y与其共轭方向X′:Y′垂直。
二 求法:
1 主方向的求法:
X:Y为主方向〈═〉X:Y与其共轭方向X′:Y′=-(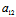 X+
X+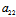 Y):(
Y):(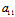 X+
X+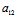 Y)
Y)
垂直〈═〉XX′+YY′=0 〈═〉X′:Y′=-Y:X
〈═〉-(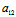 X+
X+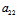 Y):(
Y):(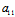 X+
X+ Y)=-Y:X
Y)=-Y:X
〈═〉X:Y=(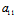 X+
X+ Y):(
Y):(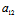 X+
X+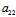 Y)
Y)
〈═〉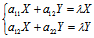 〈═〉
〈═〉 (2)
(2)
∵X,Y不全为0, ∴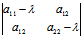 =0
=0
即 λ²-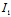 +
+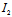 =0 (3)
=0 (3)
可见,若求二次曲线F(x,y)=0的主方向X:Y,只需先求方程(3)的根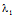 ,
,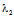 ,
,
再将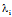 代λ(2),并解此方程组,从其非0解(X:Y),即可得到主方向X:Y。
代λ(2),并解此方程组,从其非0解(X:Y),即可得到主方向X:Y。
2 主直径的求法:
主方向求出以后,若所求的方向X:Y为非渐近主方向,则X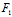 (x,y)+Y
(x,y)+Y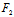 (x,y)=0便是主直径;若所求主方向X:Y不再是渐近方向,则该曲线不可能是中心二次曲线(中心曲线的渐近方向只能与其自身共轭)从而-Y:X不再是渐近方向。
(x,y)=0便是主直径;若所求主方向X:Y不再是渐近方向,则该曲线不可能是中心二次曲线(中心曲线的渐近方向只能与其自身共轭)从而-Y:X不再是渐近方向。
此时 -Y(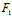 (x,y)+X
(x,y)+X (x,y))=0
(x,y))=0
便是该曲线唯一的主直径
三 特征方程与特征根:
1定义:方程(3)称为二次曲线的特征方程,其根称为曲线的特征根。
2 性质:
1°二次曲线的特征根全为实数。
事实上,△=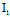 ²-4
²-4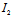 =(
=(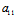 -
-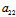 )²+4
)²+4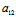 ²≥0
²≥0
2°二次曲线的特征根不全为0
事实上,若不然,则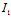 =
=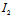 =0 即
=0 即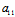 +
+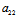 =
=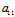
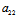 -
-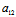 ²=0
²=0
∴-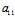 ²-
²-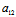 ²=0 ∴
²=0 ∴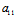 =
= =
= =0 这不可能
=0 这不可能
3 利用特征根研究主方向和主直径
定理1:主方向X:Y为渐近主方向〈═〉对应于该方向的特征根为0。
证:设主方向X:Y对应的特征根为λ,则
 X+
X+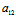 Y=λX
Y=λX
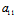 X+
X+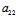 Y=λY
Y=λY
∴Φ(X,Y)=( X+
X+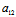 Y)X+(
Y)X+(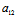 X+
X+ Y)Y=λ(X²+Y²)
Y)Y=λ(X²+Y²)
∵X,Y全为实数,且不全为0, ∴Φ(X,Y)=0〈═〉λ=0
定理2:
(i)中心二次曲线至少有两条主直径,具体地,圆的任一实直径均为主直径,非圆的中心曲线仅有两条主直径。
(ii)非中心曲线仅有一条主直径
证明:(i)若二次曲线F(x,y)=0为圆,则 =
=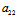 ≠0,
≠0,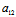 =0,从而特征根
=0,从而特征根 =
= =
=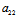 ,
,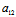 =0,则此时(2)被任意实方向X:Y所满足,即任意实方向均为主方向,从而圆的任意实直径均为主直径
=0,则此时(2)被任意实方向X:Y所满足,即任意实方向均为主方向,从而圆的任意实直径均为主直径
对于非圆的中心二次曲线,△=( -
-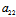 )²+4
)²+4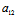 ²>0
²>0
从而曲线有不等非0实根λ1,λ2,这二实根确定的主方向为
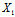 :
: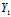 =
=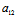 :(λ1-
:(λ1-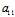 )=(λ1-
)=(λ1-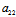 ):
):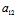
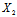 :
: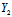 =
=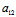 :(λ2-
:(λ2-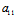 )=(λ2-
)=(λ2-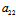 ):
):
不难证明这二主方向垂直,它们确定的主直径为
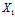
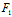 (x,y)+
(x,y)+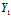
 (x,y)=0——沿
(x,y)=0——沿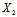 :
:
及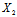
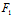 (x,y)+
(x,y)+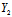
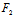 (x,y)=0——沿
(x,y)=0——沿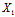 :
: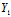
这是仅有二主直径
(ii)对于非中心曲线, =0,故其特征根λ1=
=0,故其特征根λ1=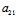 +
+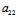 ≠0,λ=0
≠0,λ=0
∴曲线仅有一非渐近主方向X:Y,故得一主直径
X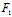 (x,y)+Y
(x,y)+Y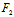 (x,y)=0
(x,y)=0
这亦是仅有的一主直径




