§7 二次曲线方程的化简与分类
一 方程的化简:
1 中心曲线方程的化简:
对中心曲线F(x,y)=0,令O′( ,
,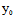 )为其中心,若将坐标原点平移至O′,则新方程中将不含一次项,再选取适当的θ角,作旋转变换,还可消去方程中的交叉乘积项,最终中心曲线的方程可化简为
)为其中心,若将坐标原点平移至O′,则新方程中将不含一次项,再选取适当的θ角,作旋转变换,还可消去方程中的交叉乘积项,最终中心曲线的方程可化简为
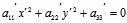 (1)
(1)
由于 , ∴
, ∴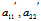 全不为0,从而中心曲线(1)关于新系的x′,
全不为0,从而中心曲线(1)关于新系的x′,
y′轴对称,即以中心曲线的二主直径作为坐标轴建立新坐标系时,则曲线的方程便简化为(1)
例1:化简二次曲线方程x²-xy+y²+4x-2y=0
解:所给二次曲线的二主直径为x+y+2=0 ,x-y+2=0
取坐标变换公式 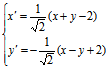
即 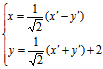
代入原方程有x′²+3y′²-8=0
即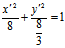
2 无心曲线方程的化简:
对无心曲线F(x,y)=0,选取适当的θ角作旋转变换,可消去方程中的交叉乘积项,即
方程简化为
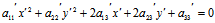
由于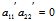 ∴
∴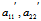 有且仅有一为0,不妨设
有且仅有一为0,不妨设 =0 ,再配方有
=0 ,再配方有
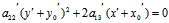
作平移
则方程最终简化为
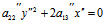 (2)
(2)
由于 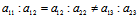 ∴
∴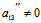
从而无心曲线(2)关于x″轴对称,即x″轴是其一主直径,且x″州与曲线的交点是新坐标系的坐标原点。
可见以无心曲线的主直径作为x′轴,以过顶点且与主直径垂直的直线作为y′轴建立新系,则曲线的方程便简化为(2)
例2:化简二次曲线方程x²+2xy+y²+2x-2y=0
解:所给曲线的一主直径为x+y=-0,曲线的顶点为原点,取过顶点且与主直径垂直的直线x-y=0,并取坐标变换,为
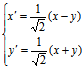
即
代入原方程并化简为 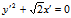
3 线心曲线方程的化简:
对于线心曲线F(x,y)=0,取一中心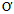 (
(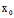 ,
,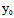 ),并作平移变换即可消去方程中的一次项,再选取适当的α角作旋转变换,还可消去交叉乘积项,最终方程简化为
),并作平移变换即可消去方程中的一次项,再选取适当的α角作旋转变换,还可消去交叉乘积项,最终方程简化为
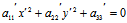
由于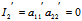 ∴
∴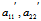 有且仅有一为0,不妨设
有且仅有一为0,不妨设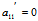 ,则线心曲线方
,则线心曲线方
程化简为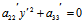 (3)
(3)
由于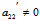 ,∴曲线(3)关于x′轴对称,可见新坐标系的x′轴是其主直径,即以曲线的一主直径作为x′轴建立新坐标系,则在新系下,曲线的方程将简化为(3)
,∴曲线(3)关于x′轴对称,可见新坐标系的x′轴是其主直径,即以曲线的一主直径作为x′轴建立新坐标系,则在新系下,曲线的方程将简化为(3)
例3:化简二次曲线方程 x²-2xy+y²+2x-2y=0
解:可以验证所给曲线是线心曲线,其主直径为x-y+1=0 再取一与主直径垂直的直线x+y=0,作坐标变换 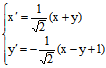
即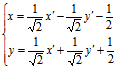
代入原方程并化简得 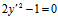
总结上述化简二次曲线方程的方法,可得如下结论:
选取适当坐标系,可使
中心二次曲线的方程的化简为 
无心二次曲线的方程的化简为 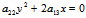
线心二次曲线的方程的化简为 
二 二次曲线的分类:
1°对于中心曲线,其方程可化简为(I)
当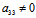 ,令
,令
A=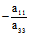 ,B=
,B=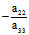 ,则(I)为 Ax²+By²=1
,则(I)为 Ax²+By²=1
若A,B>0,令A= ,B=
,B=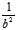 ,则(I)为
,则(I)为
[1] 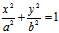 ——椭圆
——椭圆
若A,B<0,令A=-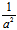 ,B=-
,B=-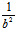 ,则(I)为
,则(I)为
[2] 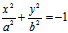 ————虚椭圆
————虚椭圆
若A>0,B<0,令A=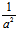 ,B=-
,B=- ,则(I)为
,则(I)为
[3] 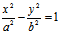 ————双曲线
————双曲线
同理当A<0,B>0时,也是双曲线
当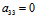 时,令A=
时,令A=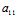 ,B=
,B= ,则(I)为
,则(I)为
[4] 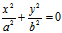 ———— 一点
———— 一点
同理,若A,B<0,则(I)也为一点
若A>0,B<0,令A=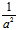 ,B=-
,B=-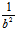 ,则(I)为
,则(I)为
[5] 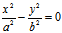 —————二相交直线
—————二相交直线
同理 若A<0,B>0,则(I)也为二相交直线。
2°对于无心曲线,其方程可化简为(II),令
P=  ,则(II)为
,则(II)为
[6] y²=2Px ——————抛物线
对于线心曲线,其方程可化简为(III),令
k= 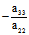 ,则(III)为 y²=k
,则(III)为 y²=k
若k>0,则(III)为
[7]y²=a² ————————二平行直线,
若k<0,则(III)为
[8]y²=-a² ————————二平行直线,
若k=0,则(III)为
[9]y²=0 ————————二重合直线。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号