§2 二次曲线的渐近方向、中心和渐近线
一 渐近方向:
定义:若一方向X:Y(即与矢量{X,Y}平行的方向)满足Φ(X,Y)=0,则称其为二次
曲线F(x,y)=0的一渐近方向。
存在性:
命题:任一二次曲线至多有二渐近方向,具体地
(i)当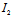 =
=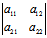 >0时,曲线有二共轭复渐近方向;
>0时,曲线有二共轭复渐近方向;
(ii)当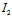 <0时,曲线有二不同实渐近方向;
<0时,曲线有二不同实渐近方向;
(iii)当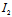 =0时,曲线有二相同实渐近方向。
=0时,曲线有二相同实渐近方向。
事实上,X:Y为渐近方向〈═〉Φ(X,Y)=0〈═〉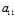 X²+2
X²+2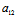 XY+
XY+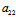 Y²=0
Y²=0
〈═〉X:Y=(-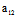 ±
± ):
):
可见,对椭圆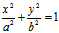 , ∵
, ∵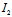 =
=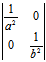 =
=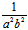 >0
>0
∴它有二共轭复渐近方向;对双曲线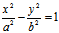 ,
,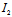 =-
=-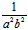 <0,
<0,
∴它有二不同实渐近方向;对抛物线y²=2px, =
=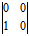 =0
=0
∴它有二相同的实渐近方向;由此,称仅有复渐近方向的二次曲线为椭圆型曲线;有二不同实渐近方向的二次曲线为双曲线型曲线;有二相同实渐近方向的二次曲线为抛物型曲线。
二 中心:
1、定义:二次曲线上任意两点间的连接线段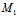
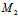 ,若不沿渐近方向,则称其为弦。若存在一点C,使得过C的任一弦均被C平分,则称C为二次曲线的中心。
,若不沿渐近方向,则称其为弦。若存在一点C,使得过C的任一弦均被C平分,则称C为二次曲线的中心。
显然:二次曲线的中心正是它的对成中心。
2、求法:
定理1:点C(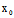 ,
,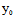 )是二次曲线F(x,y)=0之中心〈═〉
)是二次曲线F(x,y)=0之中心〈═〉 ,
,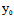 是方程组
是方程组
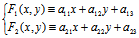 (*) 的解
(*) 的解
证:"═〉"设C(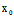 ,
,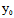 )是中心,而
)是中心,而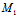
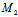 是过C的任一弦,该弦所在直线
是过C的任一弦,该弦所在直线
l: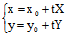 , Φ(X,Y)≠0
, Φ(X,Y)≠0
令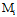 (
(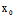 +
+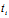 X ,
X ,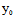 +
+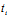 Y),i=1,2,则
Y),i=1,2,则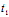 ,
,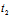 是方程
是方程
Φ(X,Y)t²+2[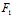 (
(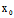 ,
,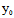 )X+
)X+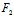 (
(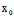 ,
,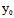 )Y]t+F(
)Y]t+F(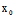 ,
,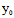 )=0的根
)=0的根
而
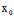 =
=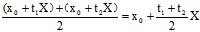
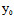 =
=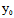 +
+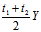 ∴
∴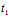 +
+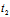 =0
=0
∴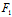 (
(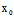 ,
,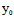 )X+
)X+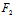 (
(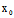 ,
,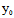 )Y=0,由弦
)Y=0,由弦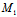
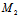 的任意性
的任意性
∴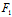 (
(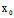 ,
,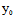 )=
)=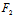 (
(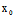 ,
,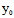 )=0
)=0
"〈═"若C(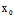 ,
,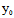 )的坐标满足
)的坐标满足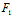 (
(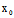 ,
,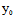 )=
)=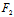 (
(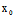 ,
,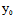 )=0 过C任取曲线的弦
)=0 过C任取曲线的弦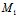
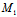 ,其方向为X:Y,从而若令
,其方向为X:Y,从而若令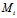 (
(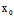 +t
+t X,
X,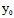 +t
+t Y),i=1,2,则
Y),i=1,2,则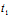 ,
,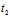 应是(*)二个根。
应是(*)二个根。
∵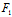 (
(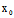 ,
,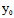 )X+
)X+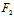 (
(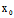 ,
,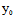 )Y=0 ∴
)Y=0 ∴ +
+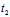 =0
=0
∵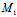
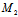 的中点坐标为
的中点坐标为
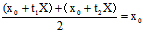
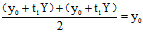
即C(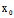 ,
,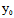 )是弦
)是弦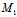
 的中点 ∴C为中心
的中点 ∴C为中心
注:若一条二次曲线有唯一中心,则称其为中心二次曲线;没有中心的二次曲线称为无心二次曲线;有不止一个中心的二次曲线称为线性二次曲线,
关于上述三种二次曲线的判别标准,我们有
定理2:
(i)二次曲线为中心二次曲线 〈═〉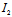 ≠0
≠0
(ii)二次曲线为无心二次曲线 〈═〉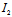 =0,但
=0,但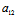 :
: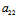 ≠
≠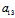 :
: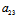
(iii)二次曲线为线性二次曲线 〈═〉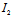 =0且
=0且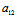 :
: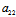 =
=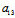 :
: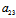
事实上,(i)二次曲线为中心二次曲线〈═〉(*)有唯一解〈═〉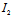 ≠0
≠0
(ii)二次曲线为无心二次曲线〈═〉(*)无解〈═〉
秩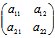 ≠秩
≠秩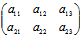 〈═〉
〈═〉
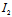 =0但
=0但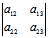 ≠0〈═〉
≠0〈═〉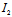 =0且
=0且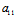 :
: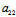 ≠
≠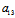 :
: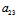
(vi)二次曲线为线性二次曲线〈═〉(*)有不止一个解〈═〉I2=0且
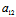 :
: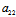 =
=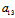 :
:
注:对线性二次曲线,由于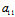 :
: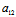 =
=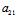 :
: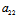 =
=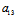 :
: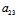 ∴方程组(*)同解于
∴方程组(*)同解于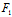 (x,y)≡
(x,y)≡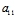 x+
x+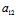 y+
y+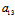 =0 即线性二次曲线的中心充满直线
=0 即线性二次曲线的中心充满直线
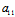 x²+
x²+ y+
y+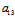 =0——中心直线
=0——中心直线
三 渐近线:
定义:过二次曲线的中心且沿其渐近方向的直线称为渐近线。
可见:椭圆型二次曲线有二共轭复渐近线;双曲型二次曲线有二不同实渐近线;而对抛物型二次曲线,若其为无心的,则其没有渐近先,若其为线性的,则由于其渐近方向为X:Y=-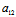 :
: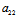 ,而这正是中心直线的方向,∴它的渐近线即为中心直线。
,而这正是中心直线的方向,∴它的渐近线即为中心直线。
求法:
法1:求出中心,再求出渐近方向即可得到渐近线的参数方程。
法2:求出中心C(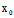 ,
,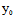 ),对渐近线上任一点M(x,y),则(x-
),对渐近线上任一点M(x,y),则(x-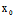 ):(y-
):(y-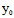 )为渐近方向, ∴Φ(x-
)为渐近方向, ∴Φ(x-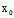 ,y-
,y-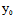 )=0
)=0
性质:
命题:二次曲线的渐近线或者与曲线不交,或者整个位于曲线上,事实上,设
l: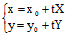 为渐近线,其中(
为渐近线,其中(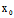 ,
,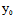 )为中心,X:Y为渐近方向
)为中心,X:Y为渐近方向
∴Φ(X,Y)=0且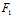 (
(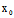 ,
,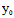 )=
)=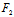 (
( ,
,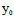 )=0,∴若F(
)=0,∴若F(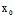 ,
,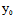 )≠0,
)≠0,
则l与曲线不变,若F( ,
,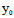 )=0,则l整个在曲线上。
)=0,则l整个在曲线上。




