第5章 二次曲线的一般理论
本章教学目的:通过本章学习,使学生在掌握二次曲线几何性质的基础上,熟悉化简二次曲线方程的各种方法,进而了解二次曲线的分类。
本章教学重点:(1)二次曲线的各种几何性质;
(2)二次曲线方程的各种化简方法;
(3)二次曲线的形状。
本章教学难点:(1)二次曲线直径、共轭直径及主直径的直观几何解释;
(2)利用坐标变换法和不变量法化简二次曲线方程。
本章教学内容:
§0 序言
一 本章的任务:
在平面直角坐标系下,二元二次方程
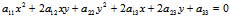
(其中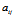 均为实数)所表示的图形,称为二次曲线。本章将通过对二次曲线方程的研究,来得到二次曲线的若干性质,然后讨论二次曲线方程的化简,最后给出二次曲线的分类。
均为实数)所表示的图形,称为二次曲线。本章将通过对二次曲线方程的研究,来得到二次曲线的若干性质,然后讨论二次曲线方程的化简,最后给出二次曲线的分类。
二 若干约定记号:
记F(x,y)≡ x²+2
x²+2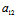 xy+
xy+ y²+2
y²+2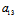 x+2
x+2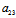 y+
y+
规定 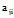 =
=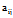 即
即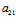 =
=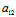 ,
,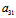 =
=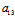 ,
,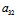 =
=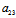
从而F(x,y)=( x+
x+ y+
y+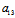 )x+(
)x+(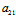 x+
x+ y+
y+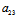 )y+
)y+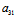 x+
x+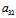 y+
y+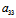
再记
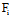 (x,y)≡
(x,y)≡ x+
x+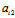 y+
y+
则 F(x,y)=x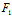 (x,y)+y
(x,y)+y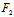 (x,y)+
(x,y)+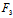 (x,y)
(x,y)
F(x,y)的系数矩阵
A=
称其为二次曲线F(x,y)=0的矩阵,由此,F(x,y)可表为
F(x,y)=(x,y,1)A
再记Φ(x,y)=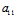 x²+2
x²+2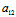 xy+
xy+ y²
y²
而矩阵 =
=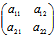 称为Φ(x,y)的矩阵
称为Φ(x,y)的矩阵
最后 ,记
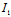 =
= +
+ ,
,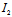 =∣A*∣,
=∣A*∣, =∣A∣,而
=∣A∣,而

 =
= +
+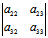
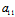 的代数余子式
的代数余子式

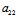 的代数余子式
的代数余子式




 浙公网安备 33010602011771号
浙公网安备 33010602011771号