§7 二次曲面的直纹性
一 定义:由一组连续变化的直线形成的曲面称为直纹面,其中每条直线都称为它的母线。
注:柱面、锥面显然都是直纹面,但椭球面,双叶双曲面与椭圆抛物面均不是直纹面。
试问,单叶双曲面与双曲抛物面是否为直纹面?答案是肯定的。
二 单叶双曲面的直纹性:
设有单叶双曲面 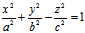 (1)
(1)
(1)等价于 (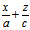 )(
)(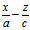 )=
)= (2)
(2)
即 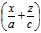 :
: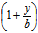 =
= :
: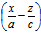 (3)
(3)
对 λ≠0,方程组
λ≠0,方程组
 (4)
(4)
表示一直线,另外
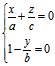 (5) 及
(5) 及
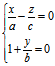 (6)
(6)
也表示直线。显然由(4)—(6)构成的直线族中每一直线均在单叶双曲面(1)上。再者对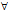
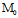 (
(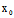 ,
,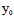 ,
, )∈(1) 有
)∈(1) 有
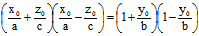
注意1+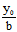 与1-
与1-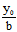 不全为0
不全为0
1°若1+ ≠0
≠0
当 ,令λ=
,令λ=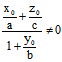
则 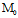 ∈(4)
∈(4)
当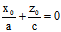 时,则1-
时,则1-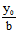 =0,则
=0,则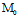 ∈(5)
∈(5)
2°若1+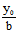 =0,则1-
=0,则1- ≠0
≠0
当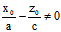 取λ=
取λ=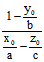 ≠0 则
≠0 则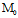 ∈(4)
∈(4)
当 时,有
时,有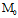 ∈(6)
∈(6)
∴有:单叶双曲面是由直线族(4)-(6)构成的 ∴单叶双曲面是直纹面。同理,由
 μ≠0 (4′)
μ≠0 (4′)
 (5′)
(5′)
及 (6′)
(6′)
组成的直线族也可构成单叶双曲面(1),为方便记忆,将(4)—(6)和(4′)-(6′)写成如下统一形式
 u,u′不全为0 (7)
u,u′不全为0 (7)
 v,v′不全为0 (7′)
v,v′不全为0 (7′)
分别称(7)(7′)为单叶双曲面(1)的u族,v族直母线。
三 双曲抛物面的直纹性:
对于双曲抛物面 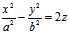 (1)
(1)
有  (2)
(2)
与单叶双曲面的情形完全类似,可以证明:直线族:
 u为任意实数 (3)
u为任意实数 (3)
可构成双曲抛物面(1) 而
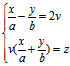 v为任意实数 (3′)
v为任意实数 (3′)
也可构成双曲抛物面 ∴(1)是直纹面,分别称(3),(3′)为双曲抛物面(1)的
u族,v族直母线。
四 单叶双曲面、双曲抛物面的直母线性质:
定理1:单叶双曲面的直母线有如下性质:
(i)同族中任二直母线异面,不同族中任二直母线共面;
(ii)过单叶双曲面(1)上某一点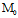 ,某一族中有且仅有一条直母线;
,某一族中有且仅有一条直母线;
(iii)经过一条直母线的某一平面也必经过属于另一族的一条直母线;
(vi)同族中任三直母线不能平行于同一平面。
证:(i)任取单叶双曲面(1)的二u族直母线
li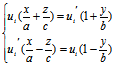 i=1,2
i=1,2
则 
=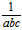
 = -
= -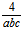 (
(
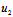 ′-
′-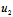
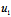 ′)≠0
′)≠0
∴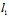 ,
, 异面 同理可证不同族中任二直母线共面。
异面 同理可证不同族中任二直母线共面。
(ii)略。
(iii)任取一u族直母线
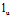 :
:
经过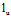 的平面π:
的平面π:
v′[u(
即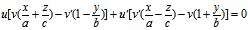
∴π过一v族直母线
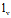 :
:
(vi)任取三u族直母线 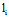 :
: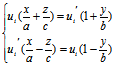 i=1,2,3
i=1,2,3
则 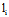 的方向矢为{
的方向矢为{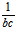 (
(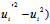 ,
,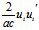 ,
, }
}
由行列式
- =

=

=-
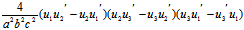 ≠0
≠0
∴三直线不平行于同一平面。
定理2:双曲抛物面的直母线有如下性质:
(i)同族中任二直母线异面,不同族中任二直母线相交;
(ii)过双曲抛物面上一任点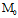 ,一族中有且仅有一直母线;
,一族中有且仅有一直母线;
(iii)同族中的所有直母线均平行于一定平面。
证:仅证(iii)对u族直母线

其方向矢为{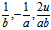 } ∴该直母线平行于平面bx+ay=0 。
} ∴该直母线平行于平面bx+ay=0 。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号