§7 直线与平面的位置关系
一 各种位置关系的解析条件:
设直线L: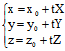 与平面π:Ax+By+Cz+D=0
与平面π:Ax+By+Cz+D=0
则 L与π相交〈═〉
 (
( ,
,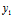 ,
,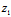 )=L
)=L π〈═〉
π〈═〉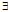 唯一的
唯一的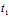 ,使
,使
A(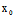 +
+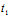 X)+B(
X)+B(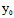 +
+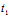 Y)+C(
Y)+C(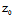 +
+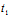 Z)=0〈═〉AX+BY+CZ≠0
Z)=0〈═〉AX+BY+CZ≠0
∴有 L与π相交〈═〉AX+BY+CZ≠0;
L∥π〈═〉不存在唯一的t使(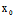 +tX)+B(
+tX)+B(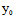 +tY)+C(
+tY)+C(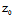 +tZ)+D=0
+tZ)+D=0
〈═〉AX+BY+CZ=0
L在π上〈═〉存在无穷多个t使A(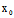 +tX)+B(
+tX)+B(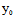 +tY)+C(
+tY)+C(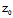 +tZ)+D=0
+tZ)+D=0
〈═〉AX+BY+CZ=A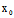 +B
+B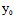 +C
+C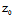 +D=0
+D=0
推论:L∥π但L不在π上〈═〉AX+BY+CZ=0,但A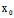 +B
+B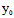 +C
+C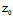 ≠0
≠0
二 直线与平面的交角:
设在直角系下,直线L与平面π的方程如上,则V{X,Y,Z}和n{A,B,C}分别是l的方向矢及π的法线矢,如图
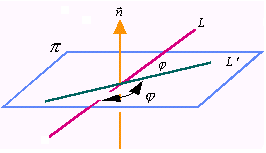
(图3.6)
令∠(L,π)=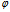 ,∠(v,n)=θ 则
,∠(v,n)=θ 则
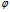 =
=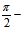 θ或
θ或 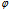 =θ-
=θ-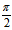 (θ为锐角)
(θ为锐角)
∴ sin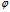 =±cosθ=∣cosθ∣=
=±cosθ=∣cosθ∣=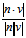 =
=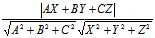
例:求过点(-1,2,-3),平行于平面6x-2y-3z+1=0且与直线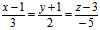 相交的直线的方程。
相交的直线的方程。
解:略。



