§ 4 空间直线的方程
一 空间直线的一般方程:
空间直线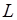 可看成两平面
可看成两平面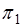 和
和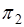 的交线.事实上,若两个相交的平面
的交线.事实上,若两个相交的平面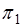 和
和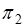 的方程分别为
的方程分别为
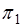 :
: 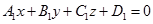
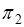 :
: 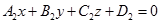
那么空间直线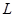 上的任何一点的坐标同时满足这两个平面方程,即应满足方程组
上的任何一点的坐标同时满足这两个平面方程,即应满足方程组
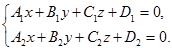 (3.4-1)
(3.4-1)
反过来,如果点不在直线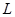 上,那么它不可能同时在平面
上,那么它不可能同时在平面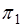 和
和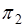 上,所以它的坐标不满足方程组(3.4-1).
上,所以它的坐标不满足方程组(3.4-1).
因此,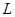 可用方程组(3.4-1)表示,方程组(3.4-1)叫做空间直线的一般方程.
可用方程组(3.4-1)表示,方程组(3.4-1)叫做空间直线的一般方程.
一般说来,过空间一直线的平面有无限多个,所以只要在无限多个平面中任选其中的两个,将它们的方程联立起来,就得到了空间直线的方程.
二 空间直线的对称式方程和参数方程:
若一非零向量平行于一条已知直线,这个向量就称之该直线的方向向量.显然,直线上的任何向量均平行于直线的方向向量。
我们知道,过空间一点可作而且只能作一条直线平行于一已知直线,因此,当直线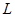 上的一点
上的一点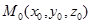 和它的一个方向向量
和它的一个方向向量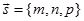 给定之后,空间直线
给定之后,空间直线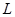 的位置就完全确定下来了.
的位置就完全确定下来了.
下面,我们来建立这种直线的方程.
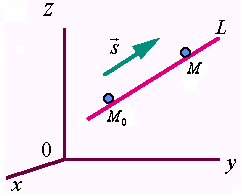
如图3-5,设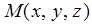 是直线
是直线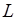 上的任一点,则
上的任一点,则 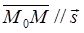 ,
,
而
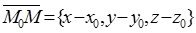 ,
,
故 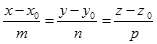 . (3.4-2)
. (3.4-2)
反过来,如果点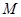 不在直线
不在直线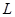 上,则
上,则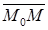 与
与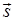 不平行,从而(2)式不成立.
不平行,从而(2)式不成立.
因此,方程组(3.4-2)就是直线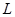 的方程.称此方程为直线的对称式方程.
的方程.称此方程为直线的对称式方程.
直线的任一方向向量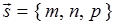 的坐标
的坐标 叫做该直线的一组方向数,而它的方向余弦叫做该直线的方向余弦.
叫做该直线的一组方向数,而它的方向余弦叫做该直线的方向余弦.
如设 
则  (3.4-3)
(3.4-3)
方程组(3.4-3)叫做直线的参数方程.
例1 用对称式方程及其参数方程表示直线

解 先找出这直线上的一点 ,如:取
,如:取  代入方程组得
代入方程组得

解此二元一次方程组得  ,
,
于是,得到直线上的一点  .
.
再找该直线的一个方向向量 ,由于两平面的交线与两平面的法线向量
,由于两平面的交线与两平面的法线向量

都垂直,可取


 ,
,
因此,所给直线的对称式方程为
 ;
;
直线的参数方程为





