§2 点与平面的位置关系
一 离差:
定义:设n°为自原点指向平面π的单位矢量,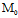 为空间中一点,自
为空间中一点,自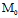 向π引垂线,垂足为
向π引垂线,垂足为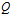 ,称
,称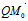 在法矢n°上的射影
在法矢n°上的射影
δ=射影n°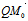 =
= 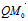 ·n°=∣
·n°=∣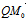 ∣cos∠(
∣cos∠(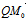 ,n°)
,n°)
=±∣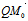 ∣
∣
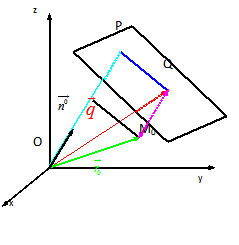 为
为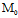 与π间的离差
与π间的离差
可见,当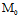 位于π的n°指向的
位于π的n°指向的
一侧时δ>0,否则δ<0
(图3.2)
计算:
命题:若平面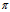 的法式方程为
的法式方程为 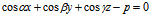 ,则
,则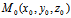 与
与 间的离差
间的离差
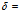

事实上,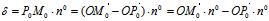
=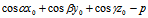
二 点到平面的距离:
设在直角坐标系下,平面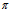 的一般方程为
的一般方程为
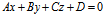 ,
,
点 到
到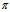 的距离
的距离
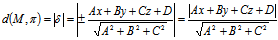 ,
,
即
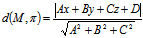 。
。
三 三元一次不等式的几何意义:
设平面π: Ax+By+Cz+D=0 则空间中任一点M(x,y,z)与π间的商差
δ=cosαx+cosβy+cosγz-P=λ(Ax+By+Cz+D)
∴Ax+By+Cz+D=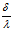
而λ是固定地,∴上式的符号取决于δ,从而有
对平面π:Ax+By+Cz+D=0一侧的点M(x,y,z),使Ax+By+Cz+D+0而对π另一侧的点M(x,y,z),使Ax+By+Cz+D<0,当然,对π上的点M(x,y,z),使Ax+By+Cz+D=0
例:证明线段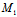
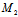 与π:5x-2y+z-1=0相交,而线段
与π:5x-2y+z-1=0相交,而线段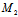
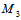 与π不交,其中
与π不交,其中
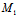 (1,0,0),
(1,0,0),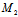 (1,4,-3),
(1,4,-3),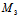 (2,5,0)
(2,5,0)
证:略




