第三章 平面与空间直线
本章教学目的:通过本章的学习,使学生掌握空间坐标系下平面、直线方程的各种形式,熟练掌握平面与空间直线间各种位置关系的解析条件,会求平面与空间直线间各种距离和夹角。
本章教学重点:(1)空间坐标系下平面、直线方程的几种重要形式;
(2)平面与空间直线间各种位置关系的解析条件;
(3)平面与空间直线各种度量关系的量化公式。
本章教学难点:(1)空间直线一般方程向标准方程的转化;
(2)综合运用位置关系的解析条件求平面、空间直线方程。
本章教学内容:
§1 平面的方程
一 方程的建立:
约定:π——表示平面;
定义:与平面π平行的一对非共线矢量,称为π的方位矢量;与π垂直的非0矢量,称为π的法线矢量,简称法矢量。
1.已知π上一点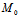 及其方位矢量
及其方位矢量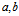 时:
时:
建立坐标系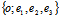 ,设
,设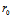 =
=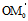 =
=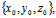 对动点
对动点 ,设
,设
r= 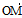 ={x,y,z},则M∈π
={x,y,z},则M∈π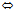
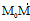 ,a,b共面
,a,b共面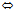 r-r。,a,b共面
r-r。,a,b共面
 =ua+vb
=ua+vb
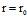 +ua+vb ————π的矢量式参数方程 (1)
+ua+vb ————π的矢量式参数方程 (1)
若令a={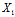 ,
,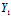 ,
,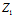 },b={
},b={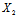 ,
,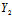 ,
,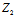 },则
},则
 ————π的坐标式参数方程 (2)
————π的坐标式参数方程 (2)
为得到π的普通方程,我们有
M∈π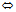
 ,a,b共面
,a,b共面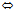
 =0 ——————π的普通方程 (3)
=0 ——————π的普通方程 (3)
(1)——(3)统称为π的点位式方程。
2。已知平面π上三非共线点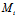 (i=1,2,3):
(i=1,2,3):
建立坐标系{O; ,
,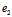 ,
,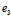 },设ri=
},设ri= 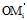 ={
={ ,
,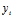 ,
,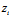 },i=1,2,3.对动点M,
},i=1,2,3.对动点M,
令
r= ={x,y,z},由(1),(2),(3)有 M∈π
={x,y,z},由(1),(2),(3)有 M∈π
r= +u(
+u( -
-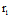 )+v(
)+v(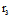 -r1) (4)
-r1) (4)
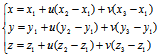 (5)
(5)
 =0 (6)
=0 (6)
(4)——(6)统称为平面的三点式方程
特别地,若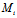 是π与三坐标轴的交点,即
是π与三坐标轴的交点,即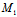 (a,0,0),
(a,0,0),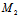 (0,b,0),
(0,b,0),
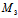 (0,0,c), (abc≠0),则
(0,0,c), (abc≠0),则
M∈π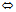
 =0
=0
即 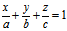 ——————π的截距式方程 (7)
——————π的截距式方程 (7)
其中a,b,c称为π在三坐标轴上的截距。
3 已知平面π上一点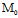 及其法矢量n:
及其法矢量n:
建立直角坐标系{O;i,j,k},设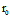 =
=  ={x。,y。,z。},n={A,B,C},
={x。,y。,z。},n={A,B,C},

(图3.1)
对动点M,令r= ={x,y,z},则
={x,y,z},则
M∈π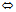
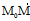 ⊥n
⊥n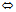 A(x-x。)+B(y-y。)+C(z-z。)=0 (8)
A(x-x。)+B(y-y。)+C(z-z。)=0 (8)
————π的点法式方程或法线式方程
特别地,若M。是自O向π所作垂线的垂足,而
n:=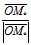 ,且记 ∣
,且记 ∣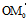 ∣=
∣=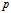 , r。=
, r。= 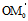 =
=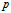 n
n
∴m∈π n(r-r。)=0
n(r-r。)=0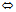 nr-nr。=0〈═〉
nr-nr。=0〈═〉
cosαx+cosβy+cosγz-P=0 (9)
其中n={cosα,cosβ,cosγ},该方程称为π的法式方程,它有如下特征:
1°一次项系数的平方和等于1;
2°常数项-P≦0。
二 平面的一般方程:
在空间坐标系下,对任一平面π,都可利用其上一点 及方位矢量a,b将其方程写成
及方位矢量a,b将其方程写成
Ax+By+Cz+D=0 (10)
其中A=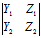 ,B=
,B=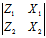 ,C=
,C=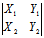
由于a{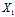 ,
, ,
,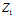 }与b{
}与b{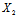 ,
,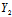 ,
, }不共线,∴(10)是一三元一次方程。
}不共线,∴(10)是一三元一次方程。
反之, 给一三元一次方程(10),不妨设A≠0,取三点
给一三元一次方程(10),不妨设A≠0,取三点
P。(-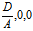 ),
),  (-
(-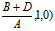 ,
, 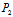 (-
(- ,
,
由于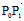 ={-
={-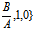 ,
, ={-
={-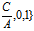
∴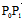 ╫
╫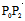 ,即
,即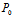 ,
, ,
, ,不共线,从而它们确定的平面π的方程为
,不共线,从而它们确定的平面π的方程为
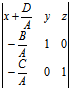 =0
=0
展开即为(10) ∴我们有
定理(平面方程基本定理):在空间坐标系下,任意平面的方程均可表为三元一次方程,而且任一三元一次方程也可表示空间中的一个平面。
称方程(10)为平面π的一般方程。
三 一般方程向法式方程的转化:
在直角坐标系下,若已知π的一般方程为Ax+By+Cz=0,则{A,B,C}是π的法矢量,
而法式方程(9)中的一次项系数是π的一特殊单位法矢量的分量。
∴若将一般方程化为法式方程只需在一般方程两边同乘以因子
λ= ±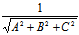 有
有
λAx+λBy+λCz+λD=0
再据λD≦0选取λ的符号即可。
例:略。




