§4 空间曲线的方程
一 普通方程
1 定义:设L为空间曲线,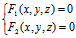 为一三元方程组,空间中建立了坐标系之后,若L上任一点M(x,y,z)的坐标都满足方程组,而且凡坐标满足方程组的点都在曲线L上,则称
为一三元方程组,空间中建立了坐标系之后,若L上任一点M(x,y,z)的坐标都满足方程组,而且凡坐标满足方程组的点都在曲线L上,则称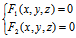 为曲线L的普通方程,又称一般方程,记作
为曲线L的普通方程,又称一般方程,记作
L: 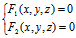
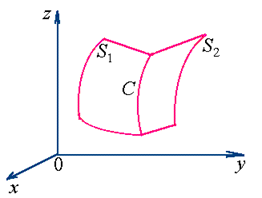
(图2.8)
注: 1°在空间坐标系下,任一曲线的方程定是两方程联立而成的方程组;
2°用方程组去表达曲线,其几何意义是将曲线看成了二曲面的交线(如图2.8);
3°空间曲线的方程不唯一(但它们同解),如
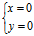 与
与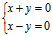 均表示z轴
均表示z轴
2 用曲线的射影柱面的方程来表达曲线
以曲线L为准线,母线平行于坐标轴的柱面称为L的射影柱面,若记L的三射影柱面的方程为 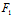 (x,y)=0,
(x,y)=0, 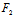 (y,z)=0,
(y,z)=0,  (z,x)=0,则
(z,x)=0,则
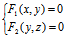 ,
,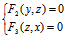 ,
,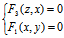
便是L的用射影柱面表达的方程
若已知曲线L: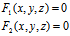 ,只需从L的方程中,分别消去x,y,z便三射影柱面
,只需从L的方程中,分别消去x,y,z便三射影柱面
的方程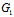 (y,z)=0,
(y,z)=0,  (z,x)=0,
(z,x)=0, 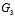 (x,y)=0
(x,y)=0
例:设有曲线L: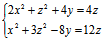 ,试求L的射影柱面,并用射影柱面方程表达
,试求L的射影柱面,并用射影柱面方程表达
曲线.
解:从L的方程中分别消去x,y,z得到
z²-4y=4z,x²+z²=4z,x²+4z=0
它们即为L的射影柱面,而
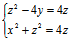 (1),
(1),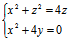 (2),
(2), 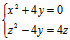 (3)
(3)
便均是L的用射影柱面表达的方程
注:利用方程(2)即可作出L的草图
二 参数方程:
1.定义:设L为一空间曲线,r=r(t),t∈A为一元矢函数,在空间坐标系下,若对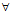 P∈L,
P∈L,
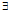 t∈A,使
t∈A,使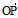 =r(t),而且对
=r(t),而且对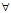 t∈A,必有P∈L,使r(t)=
t∈A,必有P∈L,使r(t)=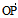 ,则称r=r(t),
,则称r=r(t),
t∈A为曲线L的矢量式参数方程,记作L=r=r(t),t∈A,t ——参数
若点r(t)={x(t),y(t),z(t)}
则称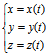 t∈A
t∈A
为L的坐标式参数方程
注:空间曲线的参数方程中,仅有一个参数,而曲面的参数方程中,有两个参数,所以习惯上,称曲线是单参数的,而曲面是双参数的。
2.求法:
例:一质点,在半径=a的圆柱面上,一方面绕圆柱面的轴作匀速转动,一方面沿圆柱面的母线方向作匀速直线运动,求质点的运动轨迹。
解:以圆柱面的轴作为z轴,建立直角坐标系{O;i,j,k},如图,不妨设质点的起始点在x轴上,质点的角速率与线速率分别为ω。,ν。,质点的轨迹为L,则对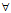
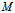 ∈L,
∈L,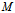 在x。y面上的投影为
在x。y面上的投影为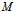 ′,
′,
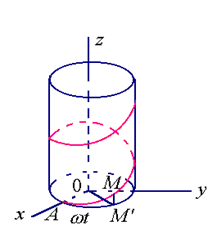
(图2.9)
r= =
= 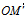 +
+ 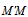 =acos
=acos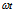 i+asin
i+asin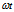 j+
j+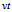 k
k
若令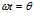 ,
,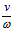 =b,则
=b,则
r=acos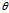 i+asin
i+asin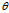 j+b
j+b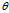 k
k 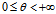
————L的矢量式参数方程
而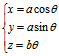
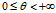
————L的坐标式参数方程,L称为圆柱螺线。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号