§3 柱面方程与柱面坐标
一 母线平行于坐标轴的柱面方程
1 定义:一动直线l在运动过程中,总是平行于一定方向V。,且总与一曲线c相交,则l的运动轨迹称为柱面,其中V。——柱面的方向,c——柱面的准线,l的任一位置——柱面的母线。
2 方程及特征:
定理:在空间坐标系下,三元方程F(x,y,z)=0为一母线,平行于z轴的柱面的方程 〈═〉该方程同解于一关于x,y的二元方程f(x,y)=0
证: "═〉"设三元方程F(x,y,z)为一母线平行于z轴的柱面Σ的方程,则Σ与 面的交线c:
面的交线c: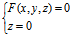 〈═〉
〈═〉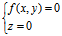
其中f(x,y)≡F(x,y,0),可以证明M(x,y,z)∈Σ〈═〉M点的坐标满足f(x,y)=0, ∴f(x,y)=0是Σ的方程,从而F(x,y,z)=0与
f(x,y)=0同解。
"〈═"若F(x,y,z)=0同解于f(x,y)=0,记以c: 为准线,母线平行于z轴的柱面为Σ,可以证明M(x,y,z)∈Σ〈═〉M的坐标满足f(x,y)=0
为准线,母线平行于z轴的柱面为Σ,可以证明M(x,y,z)∈Σ〈═〉M的坐标满足f(x,y)=0
∴f(x,y)=0表示柱面Σ,从而F(x,y,z)=0亦表示柱面Σ
例:在直角坐标系下,圆柱面 ,双曲柱面
,双曲柱面
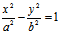 ,平面
,平面 和抛物柱面
和抛物柱面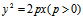 的图形如下:
的图形如下:

(图2.4)
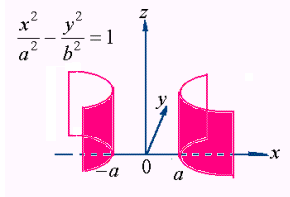
(图2.5)
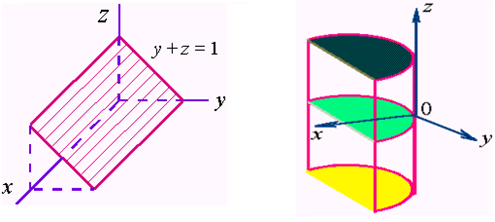
(图2.6) (图2.7)
二 柱面坐标:
1 圆柱面的参数方程:
设圆柱面Σ的中心轴重合于z轴,半径=R
对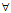 P∈Σ,记P在x.y面上的投影为P′
P∈Σ,记P在x.y面上的投影为P′
θ=∠(i,OP′),则
r=  =
=  +
+ 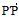 = Rcosθi+Rsinθj+uk————矢量式参数方程
= Rcosθi+Rsinθj+uk————矢量式参数方程
而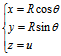 0≦θ<2π,∣u∣<
0≦θ<2π,∣u∣<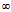 ——————坐标式参数方程
——————坐标式参数方程
2 定义:空间中建立了直角坐标系之后,对 M(x,y,z),设其到z轴的距离为ρ,则 M落在以z轴为中心轴,以ρ为半径的圆柱面上,从而
M(x,y,z),设其到z轴的距离为ρ,则 M落在以z轴为中心轴,以ρ为半径的圆柱面上,从而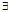 θ,u,使
θ,u,使
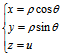 (*)
(*)
反之,对 给的ρ(ρ≥0),θ(0≦θ<2π),u(∣u∣<
给的ρ(ρ≥0),θ(0≦θ<2π),u(∣u∣< ),依据(*)式
),依据(*)式
也可确定空间中一点M(x,y,z),称有序三数组ρ,θ,u为M点的柱面坐标,记作M(ρ,θ,u)
注:1°空间中的点与其柱面坐标并非一一对应
2°曲柱面坐标求直角坐标,利用(*)即可,而由直角坐标求柱面坐标,则需按下式进行.






