§2 球面方程与球面坐标
一 球面的方程
1 定义：在空间直角坐标系下，方程（x-a）²+（y-b）²+（z-c）²=R （R为实数）
所表示的图形称为（广义）球面，其中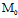
（a,b,c）称为其中心
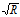称为其半径。
不难看出，广义球面包括普通球面，一个点和虚球面
2 方程的特征
定理：在空间直角坐标系下，三元方程F（x,y,z）=0为一球面的方程〈═〉
该方程同解于一个平方项系数相等，交叉乘积项消失的三元二次方程。
证："═〉"设F（x,y,z）=0为一球面Σ的方程，而由定义，Σ的方程又可
表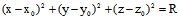
∴F（x,y,z）=0与它们同解，而它正是一平方项系数相等，交叉乘
积项消失的三元二次方程。
"〈═"设F（x,y,z）=0与一平方项系数相等，交叉乘积项消失的三元二次方程（不妨设其平方项系数均为1）
（1）
同解 ，亦即与
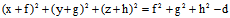（2）
同解，而（2）表示球面，∴F（x,y,z）也表示球面。
即F（x,y,z）=0是一球面的方程。
二 球面坐标（空间极坐标）
定义：空间中建立了直角坐标系之后，对空间中任一点M（x,y,z），设∣OM∣=ρ
则M在以O为中心，以ρ为半径的球面上，从而存在φ，θ，使
（*）
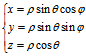反之，对任意ρ（ρ≥0），φ（0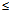
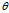
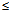π），θ（0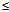
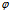<2π），通过（*）也能确定空间中一点M（x,y,z），我们称有序三数组ρ，φ，θ为M点球面坐标，记作M（ρ，φ，θ）
注：1°空间中的点与其球面坐标间并非一一对应。
2°已知M点的球面坐标，通过（*）可求其直角坐标，而若已知M的直角坐标，则通过
（**）
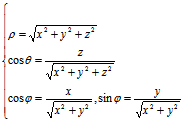便可求其球面坐标。
