§6 矢量在轴上的投影(射影)
一 空间两矢量的夹角:
设有两矢量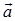 、
、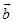 交于点
交于点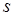 (若
(若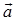 、
、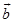 不相交,可将其中一个矢量平移使之相交),将其中一矢量绕
不相交,可将其中一个矢量平移使之相交),将其中一矢量绕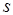 点在两向量所决定的平面内旋转,使它的正方向与另一向量的正方向重合,这样得到的旋转角度
点在两向量所决定的平面内旋转,使它的正方向与另一向量的正方向重合,这样得到的旋转角度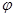 (限定
(限定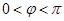 )称为
)称为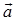 、
、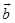 间的夹角,记作
间的夹角,记作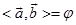 .
.
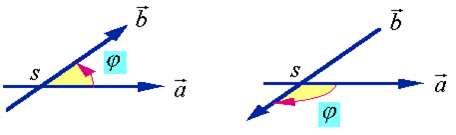
(图1.17)
若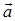 、
、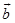 平行,当它们指向相同时,规定它们之间的夹角为
平行,当它们指向相同时,规定它们之间的夹角为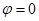 ;当它们的指向相反时,规定它们的夹角为
;当它们的指向相反时,规定它们的夹角为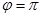 .
.
类似地,可规定矢量与数轴间的夹角.
将向量平行移动到与数轴相交,然后将矢量绕交点在矢量与数轴所决定的平面内旋转,使矢量的正方向与数轴的正方向重合, 这样得到的旋转角度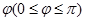 称为矢量与数轴的夹角.
称为矢量与数轴的夹角.
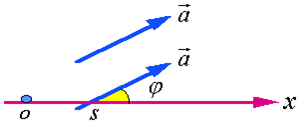
(图1.18)
二 空间点在轴上的投影:
设已知点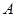 及轴
及轴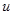 ,过点
,过点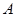 作轴
作轴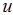 的垂直平面
的垂直平面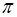 ,则平面
,则平面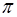 与轴
与轴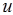 的交点叫做点
的交点叫做点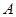 在轴
在轴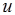 上的投影.
上的投影.

(图1.19)
三 矢量在轴上的投影:
定义1 设矢量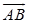 的始点
的始点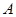 与终点
与终点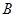 在轴
在轴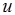 的投影分别为
的投影分别为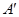 、
、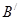 , 那么轴
, 那么轴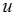 上的有向线段
上的有向线段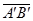 的值
的值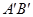 叫做矢量
叫做矢量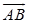 在轴
在轴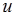 上的投影, 记作
上的投影, 记作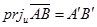 , 轴
, 轴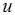 称为投影轴.
称为投影轴.
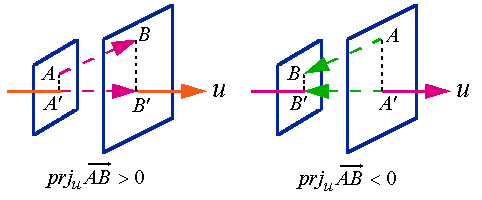
(图1.20)
这里,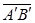 的值
的值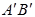 是这样的一个数:
是这样的一个数:
(1)、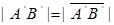 即, 数
即, 数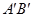 的绝对值等于向量
的绝对值等于向量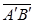 的模.
的模.
(2)、当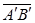 的方向与轴
的方向与轴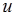 的正向一致时,
的正向一致时,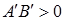 ;当
;当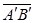 的方向与
的方向与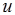 轴的正向相反时,
轴的正向相反时,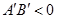 .
.
四 投影定理:
定理1 矢量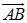 在轴
在轴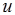 上的投影等于矢量的模
上的投影等于矢量的模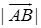 乘以轴
乘以轴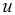 与矢量
与矢量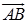 的夹角
的夹角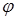 的余弦.即
的余弦.即
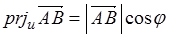 , (1.6-1)
, (1.6-1)
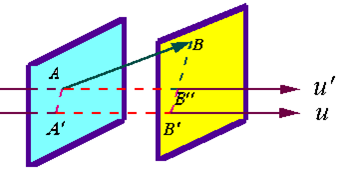
(图1.21)
证 过矢量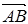 的始点
的始点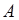 引轴
引轴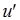 ,且轴
,且轴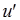 与轴
与轴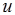 平行且具有相同的正方向,那未轴
平行且具有相同的正方向,那未轴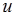 与向量
与向量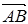 的夹角等于轴
的夹角等于轴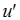 与向量
与向量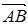 的夹角,而且有
的夹角,而且有
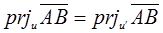
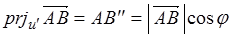
故 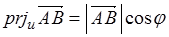
由上式可知:矢量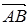 在轴
在轴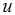 上的投影是一个数值,而不是矢量.
上的投影是一个数值,而不是矢量.
当非零矢量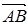 与投影轴
与投影轴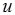 成锐角时, 向量
成锐角时, 向量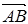 的投影为正.
的投影为正.
定理2 对于任何矢量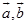 都有
都有
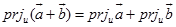 . (1.6-2)
. (1.6-2)
证 取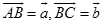 ,那么
,那么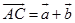 ,设
,设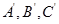 分别是
分别是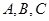 在轴
在轴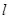 上的投影,那么显然有
上的投影,那么显然有 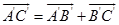 ,
,
因为 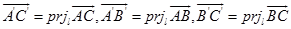
所以 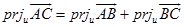 ,
,
即 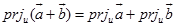 .
.
类似地可证下面的定理:
定理3 对于任何矢量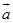 与任何实数
与任何实数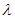 有
有
 . (1.6-3)
. (1.6-3)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号