§3 数量乘矢量
定义1 设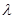 是一个数量,矢量
是一个数量,矢量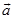 与
与 的乘积是一矢量,记作
的乘积是一矢量,记作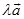 ,其模等于
,其模等于 的
的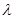 倍,即
倍,即 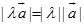 ;且方向规定如下:当
;且方向规定如下:当 时,矢量
时,矢量 的方向与
的方向与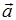 的方向相同;当
的方向相同;当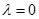 时,矢量
时,矢量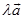 是零矢量,当
是零矢量,当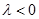 时,矢量
时,矢量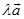 的方向与
的方向与 的方向相反.
的方向相反.
特别地,取 ,则矢量
,则矢量 的模与
的模与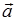 的模相等,而方向相反,由负矢量的定义知:
的模相等,而方向相反,由负矢量的定义知:  .
.
据矢量与数量乘积的定义,可导出数乘矢量运算符合下列运算规律:
定理2. 数量与矢量的乘法满足下面的运算律:
1、结合律 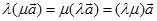 , (1.3-1)
, (1.3-1)
2、分配律
 , (1.3-2)
, (1.3-2)
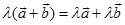 . (1.3-3)
. (1.3-3)
证 1、显然,矢量 、
、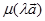 、
、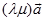 的方向是一致,
的方向是一致,
且
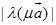 =
=  =
= =
=  .
.
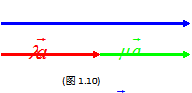
2、分配律 如图1-11
一个常用的结论:
定理3. 若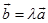 (
(  为数量 ),则矢量
为数量 ),则矢量 与向量
与向量 平行,记作
平行,记作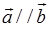 ;反之,若矢量
;反之,若矢量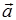 与矢量
与矢量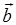 平行,则
平行,则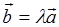 (
(  是数量).
是数量).
简言之, .
.
设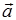 是非零矢量,用
是非零矢量,用 表示与
表示与 同方向的单位矢量.
同方向的单位矢量.
由于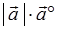 与
与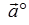 同方向,从而
同方向,从而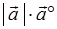 与
与 亦同方向,而且
亦同方向,而且
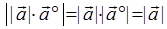 ,
,
即 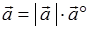 .
.
我们规定:若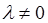 ,
,  . 于是
. 于是 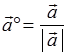 .
.
这表明:一个非零矢量除以它的模是一个与原矢量同方向的单位矢量.
请注意:矢量之间并没有定义除法运算,因此决不能将式子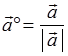 改写成形式
改写成形式 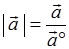 .
.
十分显然,这种错误是受实数运算法则的"惯性作用"所造成.
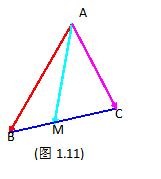
例1 设AM是三角形ABC的中线,求证
 .
.
证 如图1-12,
因为 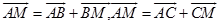 ,
,
所以 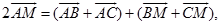
但 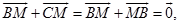
因而  ,
,
即 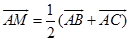 .
.




