动力学引言
- 动力学研究内容
（1）动力学研究内容
动力学研究物体的机械运动与作用力之间的关系。
在静力学中，分析了作用于物体的力，并研究了物体在力系作用下的平衡问题。在运动学中，仅从几何方面分析了物体的运动，而不涉及作用力。
动力学则对物体的机械运动进行全面的分析，研究作用于物体的力与物体运动之间的关系，建立物体运动的普遍规律。
（2）物体的抽象模型
动力学中物体的抽象模型有质点和质点系。
质点是具有一定质量而几何形状和尺寸大小可以忽略不计的物体。
如果物体的形状和大小在所研究的问题中不可忽略，则物体应该抽象为质点系。
所谓质点系是由几个或无限个相互联系的质点所组成的系统。
刚体是质点系的一种特殊情形，其中任意两个质点间的距离保持不变，也称为不变的质点系。
（3）质点动力学
认为构成复杂物体系统的基础是质点，质点是物体最简单、最基本的模型。
质点动力学基本方程描述了质点受力与其运动之间的联系。
质点动力学的基础是牛顿（Isaac Newton）总结的牛顿三定律，即惯性定律、力与加速度之间的关系的定律和作用与反作用定律。
（4）刚体动力学
认为构成复杂物体系统的质点系是刚体。
刚体动力学基本方程描述了刚体受力与其运动之间的联系。
刚体动力学的基础也是惯性定律、力与加速度之间的关系的定律和作用与反作用定律等力学定律。
（5）变形体动力学（质点系动力学）
认为构成复杂物体系统的质点系，其质点之间的距离是可以变化的。
变形体动力学基本方程描述了质点受力与其运动之间的联系，其基础也是惯性定律、力与加速度之间的关系的定律和作用与反作用定律等力学定律。
（6）连续质量力学
在连续介质假定下，质点动力学、质点系动力学和刚体动力学都是连续介质力学。
工科理论力学只研究质点动力学和刚体动力学，变形体力学已超出其关注的范围。
连续介质力学属于牛顿力学范畴。
- 动力学的形成和发展
（1）经典力学（古典力学）
牛顿对十七世纪以前的力学知识和发现的规律，
进行了理论概括，提出了运动的三大定律和万有引力定律（即任何两个物质质点都是互相吸引的，引力的
大小与两个质点的质量乘积成正比，与它们间的距离的平方成反比），建立了完整的经典力学体系。
在经典力学范畴内，认为质量是不变的量，时间
和空间是"绝对的"，与物体的运动无关。
（2）现代力学
近代（现代）物理已经证明，质量、时间、
空间都与物体运动的速度有关，当物体的速度接近光速时，经典力学的"质量观"和"时空观"不再适用。
现代力学包括经典力学、相对论力学和量子力学。经典力学指牛顿力学，是现代力学在宏观、低速情况下的特例。
爱因斯坦（A.Einstein）提出的相对论，其内容包括狭义相对论和广义相对论。
波动力学和矩阵力学统称为量子力学，它们是量子力学协调的、等价的数学表达。
（3）现代制造业的基础
在工程中，应用经典力学中的牛顿三定律，研究和解决一般机械运动问题都能得到足够精确的结果。其原因是当物体的速度远小于光速时，物体的运动对于质量、时间和空间的影响是微不足道的。
经典力学是现代制造业（包括一切机械、土木建筑、交通运输、道路工程等现代工业制造业）的基础，甚至最尖端的技术，如人造卫星、航天飞机的运动规律也没有超出经典力学的范围。
（4）动力学与生产的密切联系
动力学的形成和发展是与生产的发展密切联系的。特别是现代工业和科学技术迅速发展的今天，对动力学提出了更复杂的课题，例如高速运转机械的动力计算、高层结构受风载及地震的影响、宇宙飞行及火箭推进技术，以及机器人的动态特性等，都需要应用动力学的理论。
第11章 质点动力学基本方程
- 质点动力学
（1）质点
构成复杂物体系统的基础是质点，质点是物体最简单、最基本的模型。
（2）质点动力学基本方程
质点动力学基本方程描述了质点受力与其运动之间的联系。
（3）质点动力学的基础
质点动力学的基础是牛顿总结的牛顿三个基本定律。
这些定律是牛顿（公元1642年~1727年）在总结前人、特别是伽利略研究成果的基础上提出来的，称为牛顿三定律。
牛顿三定律适用于惯性参考系。
- 牛顿三定律
（1）第一定律（惯性定律）
第一定律反映质点具有惯性，并以其质量来度量惯性。
（2）第二定律（力与加速度之间的关系的定律）
第二定律反映质点所受的力与其加速度成比例。
（3）第三定律（作用与反作用定律）
第三定律反映质点上的作用力与反作用力等值、反向、共线，分别作用于质点和另一物体上。
- 质点动力学基本问题
（1）动力学第一类基本问题
第一类基本问题是已知质点的运动，求作用于质点的力。求解这类基本问题，需要先得到质点的加速度。
（2）动力学第二类基本问题
第二类基本问题是已知作用于质点的力，求质点的运动。求解这类问题，一般是积分过程。
（3）混合问题
综合第一类基本问题和第二类基本问题的问题，叫做质点动力学混合问题。
- 本章研究内容
（1）建立质点动力学的基本方程
根据动力学基本定律得出质点动力学的基本方
程。
（2）求解质点动力学的基本方程
运用微积分方法求解一个质点的动力学问题。
§11-1 动力学的基本定律
- 牛顿第一定律（惯性定律）
（1）牛顿第一定律的表述
不受力作用的质点，将保持静止或匀速直线运动。
（2）质点的惯性
不受力作用的质点（包括受平衡力系作用的质点），不是处于静止状态，就是其原有的速度（包括大小和方向）不变，这种性质称为惯性。
- 牛顿第二定律（力与加速度之间的关系的定律）
（1）牛顿第二定律的表述
质点的动量（即质量与速度的乘积）对时间的导数，等于作用于质点的力的大小，加速度的方向与力的方向相同。
（2）牛顿第二定律的数学表达式
（10-1）
式中m为质点的质量，v为质点的速度，F是作用在质点上的力（是汇交力系的合力）。
（3）质点动力学基本方程
在经典力学范围内，质点的质量是守恒的，式（10-1）可写为
（10-2）
上式表明，质点的质量与加速度的乘积，等于作用于
质点上的力的大小，加速度的方向与力的方向相同。
式（10-2）是质点动力学的基本方程，它建立了质点的加速度、质量与作用力之间的定量关系。式（10-2）表明，质点的质量越大，其运动状态越不容易改变，因此，质量是质点惯性的度量。
（4）重力加速度
在地球表面，任何物体都受到重力P的作用。
在重力作用下的加速度称为重力加速度，用g表示。根据第二定律有
根据国际计量委员会规定的标准，重力加速度的数值为9.80665m/s2（不同地区的数值有微小差别），一般取9.81 m/s2。
- 牛顿第三定律（作用与反作用定律）
（1）牛顿第三定律的表述：
两个物体间的作用力与反作用力总是大小相等，方向相反，沿着同一直线，且同时分别作用在这两个物体上。
（2）牛顿第三定律就是静力学的公理四，它不仅适用于平衡物体，也适用于任何运动的物体。
- 惯性参考系
质点动力学适用的参考系称为惯性参考系。在一般工程问题中，将固定于地球表面的坐标系或相对于地面作匀速直线运动（平移运动）的坐标系作为惯性参考系。
在研究地球自转的影响不可忽略的问题时，需要取以太阳为中心、三根坐标轴指向三个恒星的坐标系作为惯性参考系。本课程如无特殊说明，均采用固定在地球表面的惯性参考系。
- 力学单位
（1）国际单位制（SI）
长度、质量和时间是基本单位，分别取为m（米）、kg（千克）和s（秒）。
力的单位是导出单位。当质量为1kg的质点，
获得1m/s2的加速度时，作用于该质点上的力为
1N = 1kg×1m/s2
（2）厘米克秒制（CGS）
长度、质量和时间的单位是基本单位，分别取为cm（厘米）、g（克）和s（秒）。
力的单位是导出单位。当质量为1g的质点，获
得1cm/s2的加速度时，作用于该质点上的力为1dyn（达因），即
1dyn = 1g×1cm/s2
（3）牛顿和达因的单位换算
1N = 105dyn
§11-2 质点的运动微分方程
- 矢量形式的运动微分方程
（1）运动微分方程
质点受几个力F1，F2，…，Fn作用时，矢量形
式的运动微分方程为
（10-3）
（2）运动微分方程的另一矢量形式
（10-3a）
- 微分方程在直角坐标轴上的投影
（1）力在直角坐标轴上的投影
在计算实际问题时，需要应用式（10-3a）的投
影形式。
设矢径r在直角坐标轴上的投影分别为x，y，z，力F在直角坐标轴上的投影分别为Fxi，Fyi，Fzi。
（2）直角坐标投影表达式
式（10-3a）在直角坐标轴上的投影为
（10-4）
- 微分方程在自然轴上的投影
（1）点的全加速度
点的全加速度a在切线与主法线构成的密切面内，点的加速度在副法线上的投影等于零，即
式中
和n分别是沿轨迹切线和主法线的单位矢量，如图10-1所示。
图10-1
（2）自然轴系上的投影式
式（10-3）在自然轴系上的投影式为
（10-5）
式中Fti，Fni，Fbi分别是作用于质点上各力在切线、主法线和副法线上的投影，
是轨迹的曲率半径。
- 质点动力学的两类基本问题
（1）第一类基本问题
第一类基本问题是：已知质点的运动，求作用于质点的力。
对于第一类基本问题，只需对质点已知的运动方程求两次导数，得到质点的加速度，代入质点的运
动微分方程，即可求解第一类基本问题。
（2）第二类基本问题
第二类基本问题是：已知作用于质点的力，求
质点的运动。
对于第二类基本问题，是解微分方程，即按作
用力的函数规律进行积分，并根据问题的具体运动条件确定积分常数。
5. 例题
例10-1
曲柄连杆机构如图10-2a所示。曲柄OA以匀角速度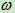
转动，OA = r，AB = l，当
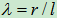比较小时，以O为坐标原点，滑块B的运动方程可近似写为
如滑块的质量为m，忽略摩擦及连杆AB的质量，求当
和
时，连杆AB所受的力。
图10-2
解：
该问题属于动力学第一类基本问题。以滑块B为研究对象，当
时，受力如图所示。
滑块B沿x轴的运动微分方程为
由题已给定的滑块B的运动方程，可通过微分求得
当
时
且
，可得
AB杆受拉力。
当
时
而
，则有
代入
，得
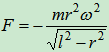
AB杆受压力。
例10-2
质量为m的质点带有电荷e，以速度v0进入强度按E = Acoskt变化的均匀电场中，初速度方向与电场强度垂直，如图10-3所示。
质点在电场中受力
作用。已知常数A，k，忽略质点的重力，试求质点的运动轨迹。
图10-3
解：
该问题属于动力学第二类基本问题。取质点的初
始位置O为原点，建立坐标系如图所示。
质点的运动微分方程在x轴和y轴上的投影式分
别为
（a）
按题意，质点运动的初始条件为：当t = 0 时
vx = v0 ，vy = 0，x = y = 0
于是，运动微分方程（a）的定积分为
得质点速度为
(b)
（b）的定积分为
得质点运动方程为
(c)
从质点运动方程(c)中消去时间t，得到轨迹方程
轨迹为余弦曲线，如图所示。
例10-3
一圆锥摆，如图10-4所示。质量m = 0.1kg的小球系于长l = 0.3m的绳上，绳的另一端系在固定点O，并与铅直线成
角。如小球在水平面内作匀速圆周运动，求小球的速度v与绳的张力F的大小。
图10-4
解：
该问题属于动力学第一类基本问题与动力学第二类基本问题的混合问题。以小球为研究的质点。作用在质点上的力有重力mg和绳的拉力F。
质点运动微分方程在自然轴上的投影式为
因为
，于是解得
绳的张力与拉力F的大小相等。
此例表明，向自然轴投影可以使动力学两类问题放开求解。
例10-4
粉碎机滚筒半径为R，绕通过中心的水平轴匀速转动，筒内铁球由筒壁上的凸棱带着上升。为了使铁球获得粉碎矿石的能量，铁球应在
时（如图10-5所示）才掉下来。求滚筒每分钟的转数n。
图10-5
解：
视铁球为质点。铁球在上升过程中，受到重力mg和筒壁的法向约束力FN、切向约束力F的作用。
质点运动微分方程在主法线上的投影式
铁球在未离开筒壁前的速度等于筒壁的速度，即
于是解得
当
时，铁球将落下，这时FN = 0，于是得
显然，
越小，要求n越大。当
时，这时
，铁球就会紧贴筒壁转过最高点而不脱离筒壁，起不到粉碎矿石的作用。
