第十七章 碰撞
教学目的
- 明确碰撞现象的特点和碰撞的基本假设。对瞬时力、恢复系数和撞击中心等概念有清楚的理解。
- 熟练的应用动量定理和动量矩定理的积分形式求解两物体对心正碰撞和饶定轴转动刚体受冲击的问题。能计算两物体对心正碰撞过程中动能的损失
本章重点、难点:
本章重点是碰撞特点,恢复稀疏的物理意义,碰撞时的基本定理及其应用。撞击中心。
一、碰撞概述
1.碰撞运动的特征及基本假定
特征:在极短的时间内物体的速度发生突变。

图17.1

图17.2
特征分析:
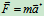
 巨大
巨大

 极小
极小
基本假定:a 在碰撞过程中,平常力忽略不计,只考虑碰撞力。
b 在碰撞过程中,位移忽略不计。
2.有局部接触变形的刚体模型 恢复系数

图17.3
恢复系数  (实验定律)表示物体变形恢复的程度。
(实验定律)表示物体变形恢复的程度。
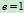 完全弹性碰撞(物体变形完全恢复)
完全弹性碰撞(物体变形完全恢复)
 弹性碰撞(物体变形不能完全恢复。即保留部分变形)
弹性碰撞(物体变形不能完全恢复。即保留部分变形)
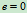 塑性碰撞(物体变形 不能恢复,即变形全部保留)
塑性碰撞(物体变形 不能恢复,即变形全部保留)
3.研究碰撞运动的普遍定理
- 用于碰撞过程的动量定理-----冲量定理
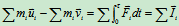
或 

2)用于碰撞过程的动量矩定理——冲量矩定理
质点: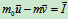
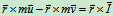
质点系
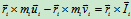
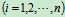


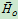 —对"O"点的冲量矩。
—对"O"点的冲量矩。
说明:矩心"O"为任意点。
4.归纳:研究碰撞运动的主要理论依据
1)基本假定
2)恢复系数 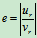
3)用于碰撞过程的普遍定理:冲量定理和冲量矩定理
二.两球的碰撞
两球的碰撞,实指两平动物体的碰撞,主要研究碰撞的速度的改变、碰撞冲量及工程应用问题。
1.两球的正碰撞
若碰撞前后两球质心速度矢量与两球心的连线重合,称为正碰撞。

图17.3
设两球质量分别为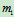 和
和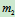 ,碰撞前的速度为
,碰撞前的速度为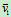 、
、 且
且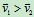 ,恢复系数为
,恢复系数为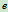 ,分析碰撞后两球的速度为
,分析碰撞后两球的速度为 、
、 ,碰撞冲量,恢复系数的简单测定,动能的损失及其应用。
,碰撞冲量,恢复系数的简单测定,动能的损失及其应用。
1)分析碰后两球的速度 、
、 。
。
研究两球的碰撞过程

 (a)
(a)
恢复系数
 (b)
(b)
联立(a)(b)两式,解得
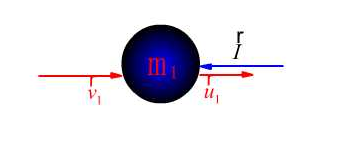
图17.4


2)分析碰撞冲量及" "的另一种意义
"的另一种意义
研究球1(或球2)的碰撞过程(图17.4)

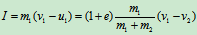
变形阶段的冲量 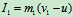 (d)
(d)
恢复阶段的冲量  (e)
(e)
其中u是两球变形阶段末的共同速度,由两球的动量守恒得
 (f)
(f)
将式分别代入式(d)、(e),有
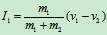 (g)
(g)
 (h)
(h)
由式(g)、(h)得
 即
即 
3)"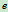 "的测定
"的测定
用待测系数的材料做成小球和很大的平板,将平板固定(图17.5)
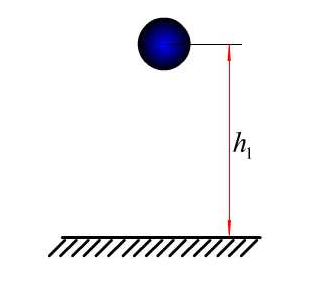
图17.5
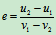
其中 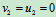

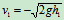
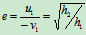
4)分析动能的损失及其应用
碰前动能 ,碰后动能
,碰后动能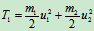 ,动能损失
,动能损失

代入 、
、 得
得
讨论: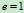 ,
,

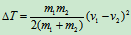
锻压应用(图17.6)锻压的效率是使锻件变形尽量大。

图17.6
取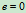

有 ,
,
锻压效率 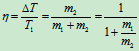 为提高效率,应使
为提高效率,应使

打桩应用(图17.7)
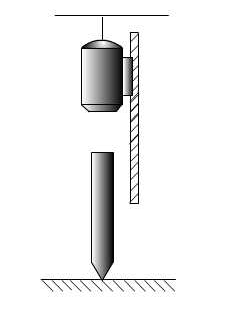
图17.7
打桩的效率是使桩获得的动能尽量大,取 、
、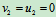 ,其效率为
,其效率为
 ,为提高效率,应使
,为提高效率,应使
例17.1 已知:如图17.8a所示,物体 自高度
自高度 处自由落下,与安装在弹簧上的物块
处自由落下,与安装在弹簧上的物块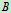 碰撞。设
碰撞。设 重
重 ,
, 重
重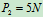 ,弹簧的刚性系数
,弹簧的刚性系数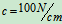 。碰撞结束后,两物体一起运动。
。碰撞结束后,两物体一起运动。
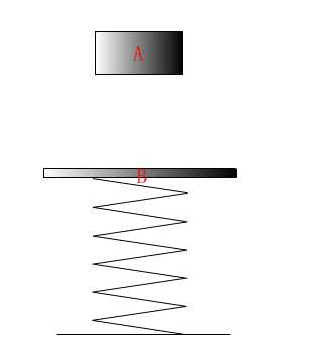
图17.8a
求:弹簧的最大变形量。
解:1 研究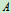 物从开始下落
物从开始下落 碰前
碰前
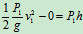
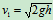
2. 研究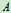 、
、 两物碰撞过程(图17.8b)
两物碰撞过程(图17.8b)
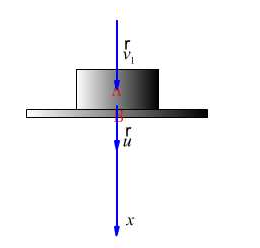
图17.8b
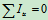

 (a)
(a)
3. 、
、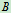 两物碰撞结束后
两物碰撞结束后 向下运动,直到速度为零
向下运动,直到速度为零
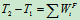
 (b)
(b)
其中 (c)
(c)
将式(a)、(c)代入(b),并化简,有

代入数据,解得
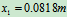
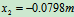
最大变形量为 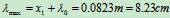
2.两球的斜碰撞
若碰撞前后的两球的质心速度矢不与两球心连线共线,则称为斜碰撞。如果碰撞的接触面是光滑的,碰撞冲量沿接触面公法线(图17.9(a)),

图17.9(a)
此时,两球的斜碰撞具有下列特征:
- 因为
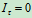 (图17.9(b))
(图17.9(b))

图17.9(b)
有  ,
,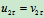
(2)两球组成的质点系,因为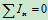 有
有
 (a)
(a)
(3)恢复系数
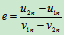 (b)
(b)
联立(a)、(b)两式,可解得 、
、 ,从而可解得
,从而可解得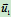 、
、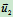 。
。
例17.2 已知:美国的"阿波罗"号飞船A与原苏联的"联盟"
号飞船B于1975年7月15日交会后实现对接(图17.10)。二者质量分别为 ,
, ,B船在惯性参考系中静止,A船的速度
,B船在惯性参考系中静止,A船的速度 ,略去飞船A、B的转动。
,略去飞船A、B的转动。 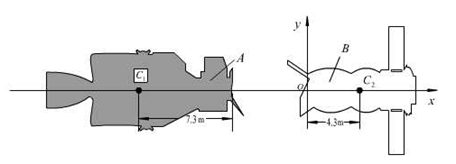
图17.10
求:1 若第一次对接是成功的,试求联合体的质心速度;
2 若第一次对接不成功,产生的碰撞的恢复系数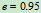 ,试求两船碰撞后的速度。
,试求两船碰撞后的速度。
解:1 第一次对接是成功的,属于塑性碰撞
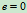
研究A、B两船,因为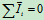 。有
。有
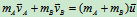 其中
其中 ,解得
,解得
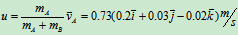
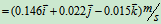
2 第一次对接是不成功的。若不考虑两船对接处的磨擦,二者在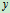 与
与 方向上的速度分量在碰撞前后不变,不
方向上的速度分量在碰撞前后不变,不


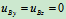
研究A、B两船,因为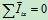 (
( 方向为公法线方向)有
方向为公法线方向)有
 (a)
(a)
恢复系数
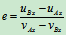 (b)
(b)
其中 ,联立(a)、(b)两式,解得
,联立(a)、(b)两式,解得


三.碰撞冲量对绕定轴转动刚体的作用 撞击中心
1.刚体角速度的变化
设绕定轴转动刚体受到外碰撞冲量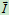 的作用,如图17.11所示。
的作用,如图17.11所示。

图17.11

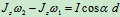

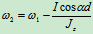
2.轴承的约束碰撞冲量 撞击中心
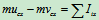 :
: 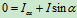
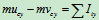 :
: 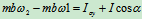
解得 
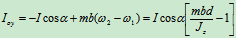
令 


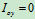


撞击中心:使轴承碰撞约束冲量为零时,外碰撞冲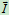 与
与 轴(OC连线)的交点"K",称为撞击中心。
轴(OC连线)的交点"K",称为撞击中心。
四.刚体碰撞举例
例17.3 已知:均质杆OA长为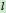 ,质量为
,质量为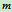 ,开始OA杆铅直,扰动后向右倒下,A端与支承B发生光滑碰撞。(图17.12),设恢复系数为
,开始OA杆铅直,扰动后向右倒下,A端与支承B发生光滑碰撞。(图17.12),设恢复系数为 。
。

图17.12(a)
求:1 OA杆回弹的角度;2 A端和轴承O的碰撞冲量。
解:1 研究杆从 到
到 碰前
碰前
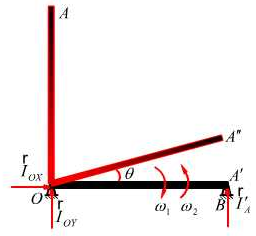
图17.12(b)

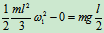
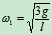
2 研究碰撞过程
 设碰后角速度为
设碰后角速度为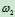
其中 


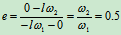
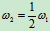
 :
: 

 :
: 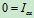
 :
: 
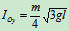
3 研究碰撞结束后,杆回到角速度为零时
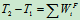

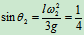

例17.4 已知:质量为 ,长度为
,长度为 的均质细杆,自水平位置无初速地自由下落,当下落高度为
的均质细杆,自水平位置无初速地自由下落,当下落高度为 时,其A端与固定刚性挂钩E碰合(图17.13),求:碰撞结束时杆的角速度
时,其A端与固定刚性挂钩E碰合(图17.13),求:碰撞结束时杆的角速度 及碰撞过程中挂钩E作用于直杆的碰撞冲量。
及碰撞过程中挂钩E作用于直杆的碰撞冲量。

图17.13(a)
解:A端与刚性挂钩E碰合后,不再分离,并迫使AB杆由平动变为转动,这称为"突出约束"问题,属于碰撞运动。
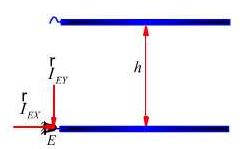
图17.13(b)
- 研究AB杆,由开始到碰前
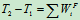
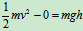

- 研究碰撞过程 AB杆由平动变为转动,有
 即
即
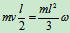
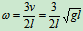
 :
: 
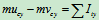 :
: 




