 第十八章 机械振动基础
第十八章 机械振动基础
教学目标:
- 掌握建立各种类型但自由度系统振动(自由振动,阻尼振动,强迫振动)微分方程的方法及其解的表达式。理解恢复力、阻尼力和激振力的概念。
- 对各种类型振动规律有清晰的理解,会计算有关的物理量。
深刻理解自由振动的固有频率(或周期)、振幅、初相位角的概念。会应用各种方法求固有频率。
了解阻尼对自由振动的影响。
深刻理解受迫振动的激振力、幅频曲线、共振和放大稀疏的概念。
- 懂得如何利用振动现象,以及消振和隔振的原理和方法。
本章重点:
单自由度系统自由振动,自由振动的固有频率和求固有频率的方法。
单自由度系统受迫振动,受迫振动的幅频曲线、共振现象。
本章难点:
衰减振动和有阻尼的受迫振动。
- 振动概述

振动:振子在平衡位置附近的往复运动
振动的力学模型:
- 电动机及其支承梁组成的系统(图18- 1)
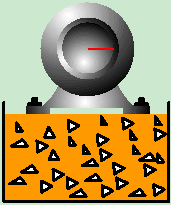
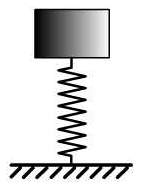
图18-1a 图18-1b
- 汽车系统(图18-2)

图18-2a 图18-2b
- 单自由度的自由振动
- 质点的自由振动微分方程及其解
设质点的质量为m,弹簧的刚性系数为c,原长为
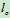 (图18- 3)
(图18- 3)

图18-3a
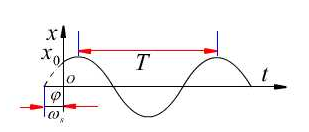
图18-3b
研究质点
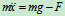
弹簧力

静变形
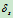
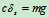
有
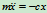
令
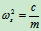
得
 (18.1)
(18.1)
其解为
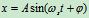 (18.2)
(18.2)
- 自由振动的特点
- 固有频率
周期T:
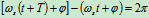
 (18.3)
(18.3)
频率
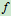 :
: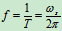
固有频率
 :
:  (圆频率)
(圆频率) 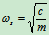 (18.4)
(18.4)
将
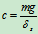 代入,得
代入,得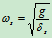
- 振幅与初相位
振幅:
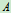 ,相位:
,相位: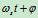 ,初相位:
,初相位:
由初始条件求
 和
和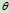
初始条件

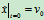
代入式(c)
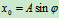
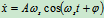
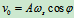
解得

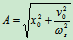

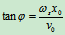 (18.5)
(18.5)
- 其它类型的单自由度振动系统
- 振动系统(图18-4)
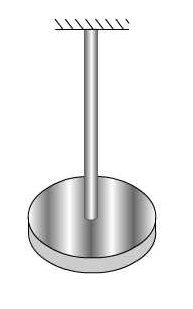
图18-4
设圆盘对中心轴的转动惯量为
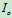 ,轴的扭转刚度为
,轴的扭转刚度为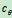
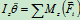
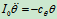

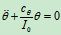
 (18.6)
(18.6)
固有频率

- 微摆动系统(图18-5)
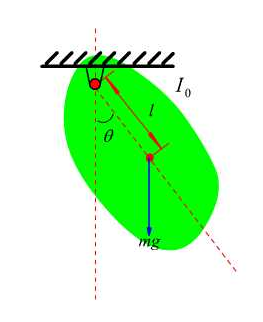
图18-5
设复摆的质量为m,对转轴的转动惯量为
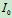 ,
,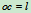
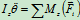

微运动,有
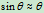 有
有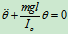
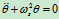
固有频率
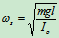
- 举例
- 设两弹簧的刚性系数分别为
 和
和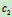 ,振动体的质量为m,试分别求两弹簧并联和串联时,系统的固有频率。
,振动体的质量为m,试分别求两弹簧并联和串联时,系统的固有频率。
解: (1)两弹簧并联(图18-6)
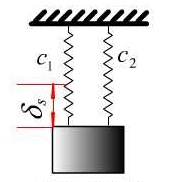
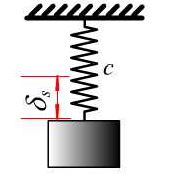
图18-6
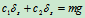

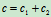
- 两弹簧串联(图18.7)
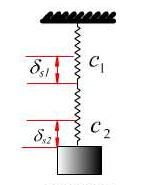
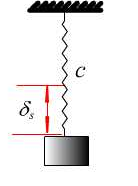
图18.7
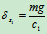

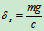

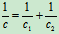
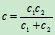
- 图18. 8所示无重弹簧梁,当其中部放置质量为m的重物时,其静挠度为
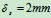 ,若将重物在梁未变形位置上无初速释放。
,若将重物在梁未变形位置上无初速释放。
求:系统的固有频率和振动规律
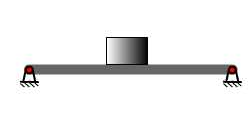
18. 8
解:(1)求
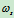 静挠度相当于弹簧静伸长
静挠度相当于弹簧静伸长
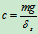

将
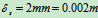 代入得
代入得
(2)振动规律
参看式(18.3)有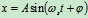
初始条件 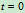 时
时 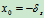
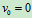
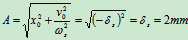

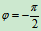
振动规律为
- 在图18.9所示重镇的系统中,摆杆
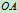 质量为m,长为
质量为m,长为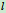 ,两弹簧的刚性系数分别
,两弹簧的刚性系数分别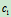 为和
为和 ,安装如图。杆在水平位置时受力平衡。
,安装如图。杆在水平位置时受力平衡。
求:系统微振动时的固有频率
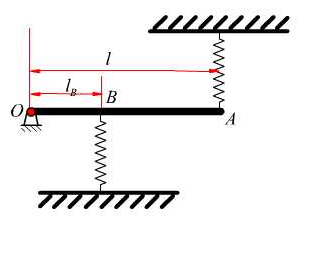
图18.9
解:研究OA杆
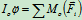
 (a)
(a)
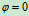 时, 由
时, 由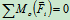
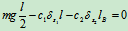 (b)
(b)
将式(b)代入式(a),有
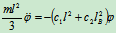
即
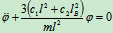
固有频率
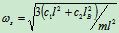
另解:用能量法求解
OA杆作自由振动时,其摆角
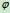 的变化规律为
的变化规律为
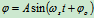
角速度
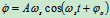

最大动能
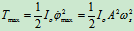
选择平衡位置为势能零位,OA杆摆过
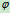 角时的势能为
角时的势能为
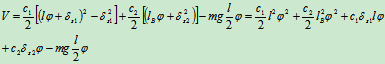
由式(b)可得


最大势能:

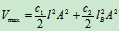
机械能守衡
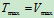
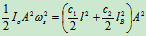
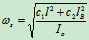
其中
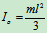

- 如图18.10均质圆柱质量为m,半径为r,在水平面上滚而不滑。连在柱心的两根水平弹簧的刚性系数各为c。
求:系统自由振动的周期
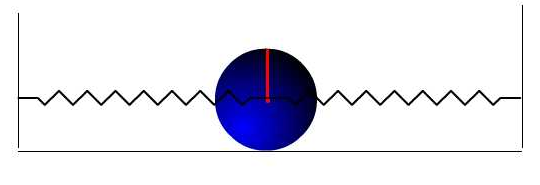
图18.10a
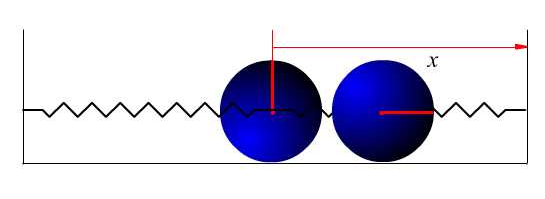
图18.10b
解:圆柱作平面运动 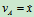
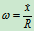
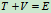
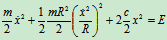
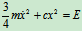
将上式对t求导,有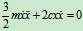
即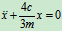
固有频率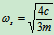
周期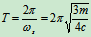
- 归纳求
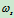 的方法
的方法
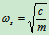 或
或
- 写出
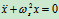 或
或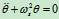 求解
求解
- 利用能量法求解




 浙公网安备 33010602011771号
浙公网安备 33010602011771号