- 刚体平面运动
教学目标
1 明确刚体平面运动的特征,掌握研究平面运动的方法,能够正确判断机构中作平面运动的刚体。
2 能熟练地应用各种方法——基点法、瞬心法和速度投影法求平面图形上任一点的速度。
3 会应用基点法求平面图形上任一点的加速度。
本章重点
以运动的分解与合成为出发点,研究求平面图形上各点的速度和加速度的基点法,以求速度为主,速度投影发与瞬心法从基点法推导出来。
本章难点
正确理解平面运动分解为随基点的平动和饶及点的转动时,选基点的意义和相对基点转动的运动特征;速度瞬新的概念。
教学过程
一、平面运动的概念
1.平面运动的概念
引例1:汽车沿直线行驶时,车轮的运动(图10.1)


车轮的运动 随着车身的平动+相对车身的转动。
引例2.曲柄连杆机构的连杆AB的运动
引例3.板擦在黑板上的任意运动

上述运动有何共性?
平面运动定义:刚体运动时其上任一点到某一固定平面的距离始终保持不变,也就是说刚体内的各点都在平行于固定平面的某一平面内运动。
2.力学模型简化
设刚体作平行于固定平面的运动
A点代表 线段的运动
线段的运动
B点代表 线段的运动
线段的运动
平面图形S代表刚体运动
结论:刚体的平面运动可以简化为平面图形在其自身平面内的运动。
3.运动方程
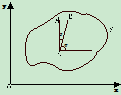
确定平面图形S在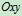 坐标系内的位置只需确定任一线段AB在
坐标系内的位置只需确定任一线段AB在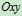 中的位置确定AB线段的位置,需确定坐标
中的位置确定AB线段的位置,需确定坐标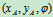 ,A点称为基点。所以平面运动的运动方程:
,A点称为基点。所以平面运动的运动方程:
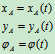 (10.1)
(10.1)
其上任一点M的运动方程为
 (10.2)
(10.2)
式中AM的长度和 是常量,所以只要方程(10.1)确定,M点的运动就可确定。
是常量,所以只要方程(10.1)确定,M点的运动就可确定。
4.运动的分解及分解运动的特性分析
特例分析:在方程(10.1)中,若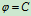 则"S"作平动 ,若
则"S"作平动 ,若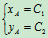 则"S"作定轴转动一般情况下,平面运动可以看成为由平动和定轴转动的合成。
则"S"作定轴转动一般情况下,平面运动可以看成为由平动和定轴转动的合成。
运动分解:研究对象:平面图形S
静系:固定平面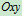 。
。
动系: (其中A是"S"上一点,
(其中A是"S"上一点,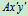 伴随A作平动,是虚构的一坐标系)。
伴随A作平动,是虚构的一坐标系)。
牵连运动:动系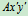 随A点平动。
随A点平动。
相对运动:绕A点转动
所以,平面运动 随基点A平动+相对基点A转动。
分解运动特性:
平动:随基点的不同而不同
转动:相对不同基点转过的角位移、角速度和角加速度都是相同的,即转动与基点选择无关。
证明1:
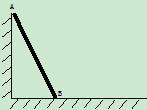
证明2:
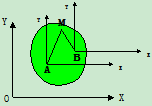
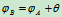
 常量
常量
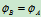
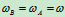
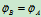
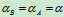
二.平面图形的角速度及图形上各点速度分析
1.基点法(合成法)
平面运动随基点平动+相对基点的转动设已知A点速度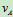 和角度
和角度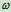 求图形上任一点B的速度。
求图形上任一点B的速度。
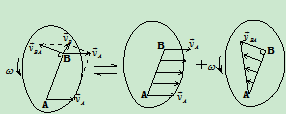
B点的速度为: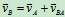 (10.3)
(10.3)
式中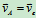 ,,其中
,,其中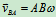
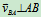 ,式(10.3)只能求2个求知量,通常的已知量
,式(10.3)只能求2个求知量,通常的已知量
为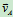 和
和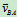 的方向。
的方向。
式(10.3)也可用矢量求导得到,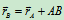 其中
其中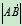 是常量。
是常量。
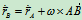
其中 ,
,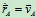 ,
,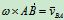 ,也即
,也即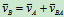
2.速度投影法
将式(10.3)向AB连线和AB连线的正垂向投影,有
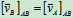 (10.4)
(10.4)
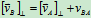
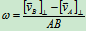 (10.5)
(10.5)
式(10.4)称为速度投影定理,是刚体不变形的属性,式(10.5)中的正垂向投影过B点作逆时针转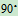 的射线为正方向,如图10.9中的
的射线为正方向,如图10.9中的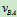 所指的方向。
所指的方向。
例10.1如图11所示,在曲柄连杆机构中,已知曲柄OA长为R,绕O轴以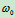 逆时针转动,求
逆时针转动,求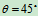 ,
,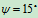 时,滑块B的速度
时,滑块B的速度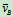 及连杆AB的角速度
及连杆AB的角速度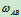 。
。
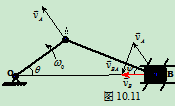
解:1. 分析运动:
OA杆定轴转动,AB杆作平面运动
2.分析速度
OA杆: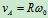 ,AB杆:
,AB杆: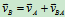
只有2个未知量,可求解,由速度合成图11,有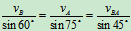
求得 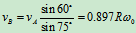 ,
,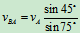
而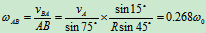
另解:用速度投影法:
AB: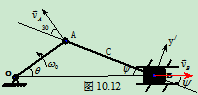
设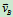 方向如图10.12所示
方向如图10.12所示
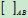 :
: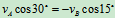
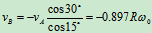 (负号说明与假设相反)
(负号说明与假设相反)
 (
( 轴指向为正)
轴指向为正)

 (负号说明
(负号说明 是顺时针转向的)
是顺时针转向的)
问题,若求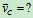 (C点是AB杆的中点)
(C点是AB杆的中点)
例10.2在图10.13所示的平面机构中,已知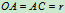 ,
,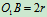 ,
,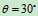 ,OA杆以
,OA杆以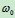 绕O轴匀速转动,在图示位置时,OA、CB沿水平方向,
绕O轴匀速转动,在图示位置时,OA、CB沿水平方向,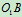 、AC沿铅垂方向,试求此瞬时(1)
、AC沿铅垂方向,试求此瞬时(1)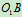 杆的角速度
杆的角速度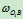 。(2)板上C点速度
。(2)板上C点速度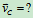 。
。
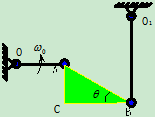
解:1.分析运动
OA杆, 杆定轴转动
杆定轴转动
ABC作平面运动
2.分析速度
OA: 
ABC: 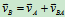
由速度合成图:
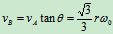
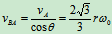
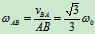
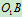 :
: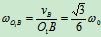
3.求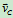
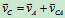 其中
其中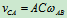
由图10.13: 
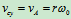
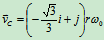
问题:若不分析B点速度,求出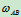 ,能否求出
,能否求出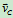 ?
?
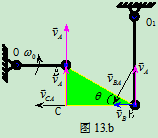
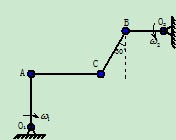
例10.3图10.14中给出一种平面铰接机构,已知杆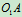 的角速度是
的角速度是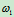 ,杆
,杆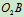 的角速度是
的角速度是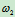 ,转向如图10.14所示。在图示瞬时,杆
,转向如图10.14所示。在图示瞬时,杆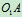 铅直,杆AC和
铅直,杆AC和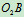 水平,而杆BC对铅直线成偏角
水平,而杆BC对铅直线成偏角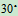 ,又
,又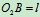 ,
, 。试求该瞬时点C的速度。
。试求该瞬时点C的速度。
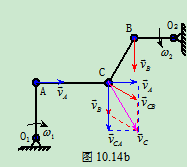
解:1 分析运动
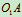 、
、 杆作定轴转动,
杆作定轴转动,
AC、BC杆作平面运动。
2 分析速度
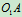 :
: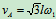
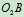 :
: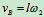
AC: 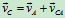 (a)
(a)
BC: 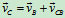 (b)
(b)
由式(a)、(b)得:
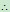
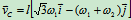
3. 速度瞬心法
引言: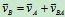 ,若
,若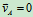 ,则
,则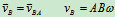
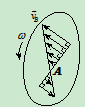
此时图形上各点速度分布如图10。15所示
速度瞬心:某瞬时平面图形上速度为零的那一点称为该瞬时平面图形的瞬时速度中心,简称为速度瞬心,通常用"P"表示。
定理:一般情况下,每瞬时平面图形上速度瞬心是唯一存在的。
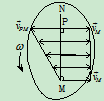
证明:设已知平面图形上任一点M的速度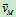 和平面图形的角速度
和平面图形的角速度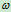 ,
,
过M点作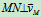 如图10.16所示,MN上一点P的速度为:
如图10.16所示,MN上一点P的速度为:

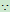
 与
与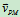 方向相反.
方向相反.
∴ 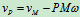 当
当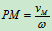 时,
时,
当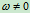 时,
时,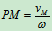 只有一个确定的值,且只能在MN直线上有满足此条件的点,所以定理得证。
只有一个确定的值,且只能在MN直线上有满足此条件的点,所以定理得证。
找瞬心的几种方法:
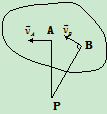
1)已知两点速度方向
a)  ∥
∥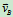
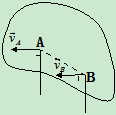
b) 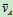 ∥
∥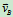 且
且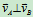 瞬时平动
瞬时平动
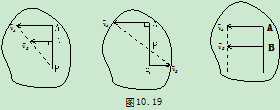
c)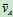 ∥
∥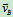 且
且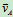
 时,需知
时,需知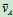 、
、 的大小(图10.19)
的大小(图10.19)
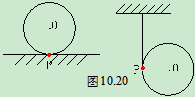
2)已知平面图形沿某一线或面纯滚,接触点瞬心(图10.20)