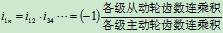第八章 刚体基本运动
教学目标
1 明确刚体平动和刚体定轴转动的特征。能正确地判断作平动的刚体和定轴转动的刚体。
2 对刚体定轴转动时的转动方程、角速度和角加速度及它们之间的关系要有清晰的理解。熟知匀速和匀变速转动的定义和公式。
3 能熟练地计算定轴转动刚体上任一点的速度和加速度。
4 掌握传动比的概念及其公式的应用。
5 对角速度矢、角加速度矢、以及用矢积表示刚体上一点的速度与加速度有初步的了解。
本章重点
刚体平动及其运动特征
刚体的定轴转动,转动方程、角速度和角加速度
定轴转动刚体上任一点的速度和加速度。
本章难点
用矢积表示刚体上一点的速度与加速度。
教学过程
研究刚体运动时:首先要了解每种运动形式的特征,并研究整个刚体的描述方法,然后再研究刚体上各点的运动。
- 刚体平动
先看几个实例:
实例1 汽车沿直线行驶时车身的运动;

实例2 推拉窗户的运动;
实例3 游乐车车厢的运动;

- 定义:刚体运动时,其上任一直线始终与原位置平行。
- 特征分析
运动方程

 是常矢量
是常矢量
轨迹:形状相同
速度:
 ,
,
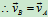
加速度:
 ,
,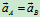
结论:研究刚体的平动,可归结为研究其上任一点的运动。
- 平动分类
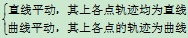
演示机构运动  、
、 //
//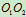 ,
,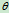 角不变并画出
角不变并画出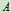 、
、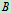 、
、 点的轨迹,以
点的轨迹,以 为圆心
为圆心 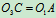 为半径的圆
为半径的圆
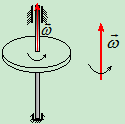
二.刚体定轴转动
实例分析
实例1 门绕其转动的轴转动
实例2 风车上的叶片绕其转轴转动


- 定义:刚体运动时,其上有一直线始终保持不动,其余各点均作圆周运动。
- 整体运动描述

位置确定:转角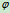
转动方程: 单值连续函数
单值连续函数
角速度:
角加速度:
 、
、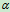 均为代数量,其正﹑负号表示刚体的转向,从轴正向往负向看
均为代数量,其正﹑负号表示刚体的转向,从轴正向往负向看 逆时针为正,顺时针为负。
逆时针为正,顺时针为负。
开始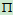 平面与
平面与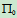 平面重合
平面重合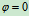 ,然后刚体转动至图示位置,画出转角
,然后刚体转动至图示位置,画出转角
特例:(1)若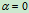 ,
,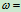 常量,称为匀速转动,此时
常量,称为匀速转动,此时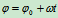 ,
,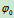 是
是 时的转角
时的转角
(2)若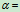 常量,称为匀变速转动,此时
常量,称为匀变速转动,此时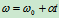 ,
, ,
, 、
、 是
是 时的转角和角速度
时的转角和角速度
- 转动刚体上各点运动分析
自然坐标法
运动方程: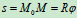
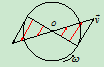
速度: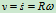 ,
, 指向如图所示。半径上各点速度分布如图
指向如图所示。半径上各点速度分布如图
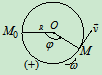
加速度:切向加速度 ,
, ,指向如图所示
,指向如图所示

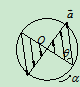
法向加速度  方向
方向 ,
,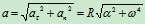 ,
, 任一半径上各点加速度分布如图
任一半径上各点加速度分布如图
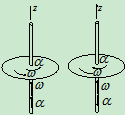
- 角速度﹑角加速度的矢量表示点的速度和加速度的矢量表示
- 有限转动不是矢量,无限转动是矢量
描述转动刚体位置的转角虽然有三个要素:转轴在空间的方位,转角的大小和转角的转动方向,但实践证明转角不能用矢量表示。如图所示
原来位置
先绕
 轴正向转90 后绕
轴正向转90 后绕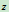 轴正向转90
轴正向转90
先绕
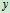 轴正向转90 后绕
轴正向转90 后绕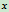 轴正向绕90
轴正向绕90
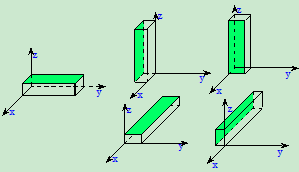
但无限转动可用矢量表示,即
 (证明略)
(证明略)
- 角速度﹑角加速度的矢量表示,
角速度矢量 的表示:方位沿转轴,大小等于角速度的绝对值
的表示:方位沿转轴,大小等于角速度的绝对值 ,指向由右手定则定,它表示角速度的转向,如图
,指向由右手定则定,它表示角速度的转向,如图
如以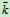 表示沿转轴的单位矢量,则
表示沿转轴的单位矢量,则 式中
式中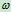 为
为 在转轴上的投影是代数量,角加速度为
在转轴上的投影是代数量,角加速度为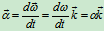
即角加速度矢量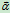 也沿转轴,表示方法
也沿转轴,表示方法 与类似,如图所示
与类似,如图所示
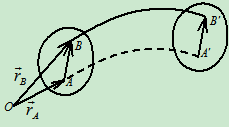
- 各点速度﹑加速度的矢量表示
在转轴上任取一点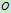 ,向点
,向点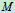 引矢径
引矢径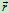 如图
如图
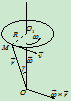

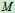 点的速度可表示为
点的速度可表示为

证明: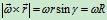
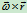 的方向垂直于
的方向垂直于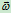 ,
, 确定的平面即垂直于转动半径
确定的平面即垂直于转动半径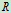 ,指向用右手定则判定,与自然法分析的分析的速度方向一致,所以式
,指向用右手定则判定,与自然法分析的分析的速度方向一致,所以式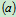 成立。
成立。
由第七章点的运动学知: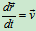
所以可得出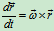
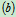
式 表示了大小不变,只是方向变化的矢量
表示了大小不变,只是方向变化的矢量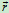 的导数公式,由此,可得出泊桑公式:
的导数公式,由此,可得出泊桑公式: ,
,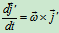 ,
,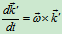
其中 ,
,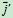 ,
,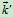 是固连于转动刚体上的三个单位矢量。
是固连于转动刚体上的三个单位矢量。
将式对时间求一次导数,可得加速度公式,即
其中 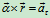 切线加速度,
切线加速度,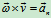 法向加速度
法向加速度
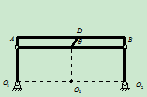
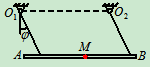
例8.1荡木用两条等长的钢索平行吊起,如图所示,钢索长为 ,长度单位为
,长度单位为 ,当荡木摆动时,钢索的摆动规律为
,当荡木摆动时,钢索的摆动规律为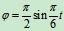 ,其中
,其中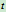 以
以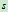 计,试求当
计,试求当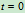 和
和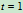 时荡木中点
时荡木中点 的速度,加速度
的速度,加速度
解
- 运动分析:
 //
// ,
, 荡木作平动,
荡木作平动, 点与
点与 点的运动相同
点的运动相同
- 研究钢索
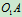 ,当钢索拉紧时,就相当于刚性杆绕转轴
,当钢索拉紧时,就相当于刚性杆绕转轴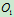 转动
转动


当 时
时 
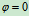 ,
,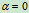
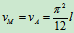

 方向如图
方向如图
当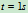 时
时  ,
, ,
,
 ,
,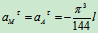
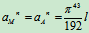 方向如图8.20
方向如图8.20
- 齿轮传动是常见的轮系传动方式之一,可用来提高或降低转速,可用来改变转向。两齿轮外啮合时,其转向相反图(8.21
 );而内啮合时,其转向相同(图
);而内啮合时,其转向相同(图 )。设齿轮1和齿轮2的节圆半径分别为
)。设齿轮1和齿轮2的节圆半径分别为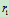 和
和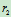 ,齿轮1的角速度
,齿轮1的角速度 和角加速度分别为
和角加速度分别为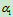 ,求齿轮的角速度
,求齿轮的角速度 和角加速度
和角加速度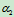 ?
?

解 两齿轮啮合时,由于两节圆的接触点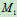 、
、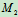 间无相对滑动,故
间无相对滑动,故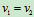 并且速度方向也相同,即
并且速度方向也相同,即 ,
,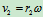 有
有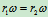
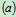
将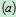 式对时间求一次导数,
式对时间求一次导数,
有
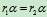

从式 和
和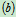 ,可得到齿轮2的角速度和角加速度
,可得到齿轮2的角速度和角加速度
 ,
,
在机械工程中,常常把主动轮和从动轮的两个角速度的比值称为传动比,用附有角标的符号表示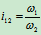 由齿轮的节圆半径
由齿轮的节圆半径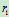 、
、 或齿轮的齿数
或齿轮的齿数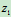 、
、 ,齿轮在啮合圆上的齿距相等,它们的齿数与半径成反比),可表示为
,齿轮在啮合圆上的齿距相等,它们的齿数与半径成反比),可表示为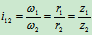

几点说明:
- 式的定义的传动比是两个角速度大小的比值,与转动方向无关,因此不仅适用于圆柱齿轮传动,也适用于传动轴成任意角度的圆锥齿轮传动﹑摩擦轮传动或不计厚度的皮带轮的传动。
- 有时为了区分轮系中各轮的转向,对各轮都规定统一的转动正向,这时各轮的角速度可取代数值,从而传动比也取代数值。
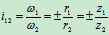
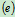
式中正号表示主动轮与从动轮转向相同(内啮合)如图8.21 ,负号表示转向相反(外啮合)如图
,负号表示转向相反(外啮合)如图
- 减速箱由四个齿轮构成如图所示。齿轮Ⅱ和安装Ⅲ在同一轴上,与轴一起转动。各齿轮的齿数分别为
 ,
,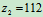 ,
, 。如主动轴Ⅰ的转速
。如主动轴Ⅰ的转速 ,试求从动轮Ⅳ的转速
,试求从动轮Ⅳ的转速 ?
?
解:用 、
、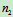 、
、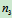 和
和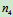 分别表示各齿轮的转速,于是有
分别表示各齿轮的转速,于是有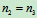 ,应用上例中的式
,应用上例中的式 ,有
,有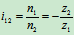 ,
,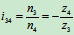
于是有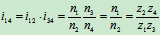
代入数值得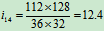 (正值说明轮Ⅳ与轮Ⅰ转向相同)
(正值说明轮Ⅳ与轮Ⅰ转向相同)
从动轮Ⅳ的角速度为-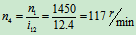
若 级传动,有
级传动,有 对外啮合齿轮
对外啮合齿轮 ,
,
则