 第二篇运动学
第二篇运动学
本篇教学目标
1 能选用合适的方法描述点的运动与刚体的基本运动。能熟练计算速度和加速度、角速度和角加速度,包括简单机构的运动分析。
2 对运动的相对性有比较清晰的概念。掌握点和刚体的运动合成与分解方法。在具体的问题中能恰当地选取动点和动参考系,会正确运用合成法,求解符合运动中点的速度和加速度问题以及平面运动图形上各点的速度与加速度。
本篇重点
分析计算各种情况下点的速度和加速度;运动的合成与分解的方法。重点的章节是点的复合运动与刚体的平面运动。
本篇难点
牵连速度、牵连加速度和哥氏加速度的概念,以及相对运动的分析和运动合成的方法。
运动学概述:
运动学的任务:研究物体运动的几何性质,包括物体运动时位置的确定,点运动的轨迹,速度,加速度等。
力学模型:点,刚体。
参照物:本文约定,若不特别指明,参照物应是地球。
第七章 点的运动学
教学目标
1 能用矢量法建立点的运动方程,求速度和加速度。
2 能熟练地应用直角坐标法建立点的运动方程,求轨迹、速度和加速度。
3 能熟练地应用自然法求点在平面上作曲线运动时的运动方程、速度和加速度,并正确理解切向加速度和法向加速度的物理意义。
本章重点
1 点的曲线运动的直角坐标法,点的运动方程,点的速度和加速度在直角坐标轴上的投影。
2 点的曲线运动的自然法,点沿已知轨迹的运动方程,点的切向加速度和法向加速度。
本章难点
矢量求导及自然轴系的概念。
教学过程
本章介绍描述点运动常用的四种坐标法。
一﹑矢量法
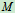 点位置确定
点位置确定
运动方程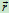 =
=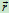
 单质﹑连续函数,轨迹:矢端曲线
单质﹑连续函数,轨迹:矢端曲线
举例:另出画面 ,探照灯照飞机,动画演示
飞机 光柱 灯
速度 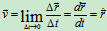
 方向沿轨迹切线
方向沿轨迹切线
加速度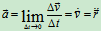 方向沿速度端图切线(图3)
方向沿速度端图切线(图3)
(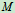 点动
点动 跟着变化最后到
跟着变化最后到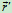 ,
,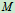 )
)
二﹑直角坐标法
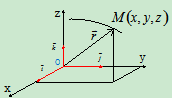
 点位置确定
点位置确定
运动方程
 单质连续
单质连续
轨迹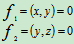



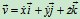
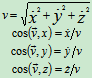

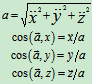
三 自然坐标法
前提:点的轨迹已知
显示火车沿轨迹行驶的一段动画

弧坐标的建立:在轨迹上确定 点,规定"+","-"
点,规定"+","-"
 点位置确定:弧坐标S
点位置确定:弧坐标S
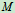 (—) (+)
(—) (+) 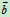

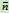 付法线,主法线
付法线,主法线
轨迹
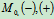

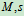
 切线,主法线,付法线
切线,主法线,付法线
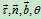
动画显示 点运动时,
点运动时, 跟着一起动。
跟着一起动。
运动方程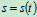 单质连续函数自然轴系
单质连续函数自然轴系
 :沿
:沿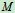 点轨迹的切线,指向"+"
点轨迹的切线,指向"+"
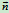 :沿主法线(过曲率中心)指向曲线凹向
:沿主法线(过曲率中心)指向曲线凹向
 ,沿付法线,且
,沿付法线,且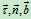 组成右手坐标系
组成右手坐标系


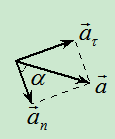
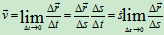
 =
=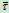
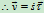


加速度:
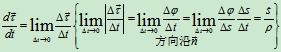
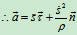
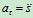 切向加速度
切向加速度
 法向加速度
法向加速度
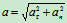
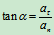
四 极坐标:点在做平面曲线运动时,还可有极坐标表示
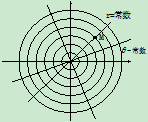

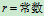
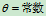
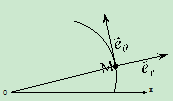
极坐标的建立(如图): 极点,
极点, —极轴,
—极轴,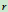 —极半径,
—极半径,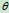 —幅角,
—幅角,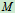 点位置的确定
点位置的确定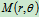
运动方程:
极坐标的单位矢量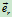 ,
,
(在图中,显示当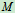 点沿径向
点沿径向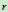 移动时,
移动时, ,
, 随之变动的情形,再显示
随之变动的情形,再显示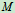 点随幅角运动时,
点随幅角运动时,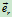 ,
, 随之运动的情形)
随之运动的情形)

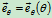
先求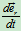 和
和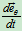




速度:由 ,有
,有 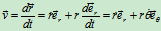
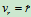 径向速度
径向速度  横向速度
横向速度
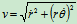 方向tan
方向tan =
= 如图
如图
加速度::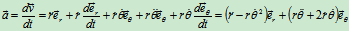
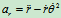 径向加速度
径向加速度  横向加速度
横向加速度
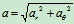
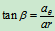 (如图)
(如图)
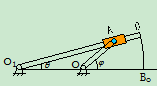
- 在曲柄摇杆机构中,曲柄
 与水平线夹角的变化规律为
与水平线夹角的变化规律为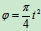 ,设
,设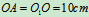 ,
,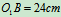 ,求
,求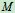 点的运动方程和
点的运动方程和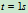 时
时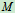 点的速度和加速度(演示图中机构的运动可将
点的速度和加速度(演示图中机构的运动可将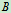 点的轨迹画出来)
点的轨迹画出来)
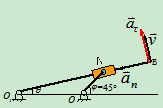
解法1 自然坐标法
 点的运动方程
点的运动方程

速度 
加速度 
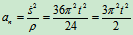
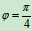
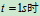
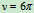
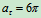
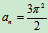
解法2 直角坐标法(坐标建立如图)

B点的运动方程: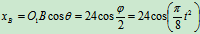

速度: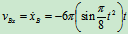

加速度: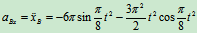
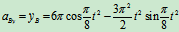
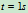 时
时 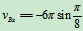
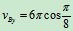
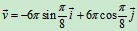
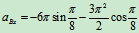
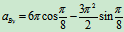

解法3 极坐标法(坐标建立如图)
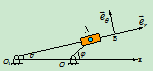
 点的运动方程:
点的运动方程:
速度:

加速度: 
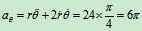
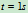 时
时 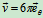
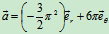
- 半径为
 的圆轮在地上沿直线匀速滚动,已知轮心的速度为
的圆轮在地上沿直线匀速滚动,已知轮心的速度为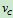 试求轮缘上一点
试求轮缘上一点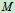 的运动方程﹑轨迹﹑速度和加速度(演示图轮在地面上纯滚动)
的运动方程﹑轨迹﹑速度和加速度(演示图轮在地面上纯滚动)
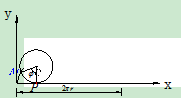
解:建立直角坐标如图19, 时
时 点位于
点位于 点
点
 点的运动方程:
点的运动方程: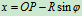 其中
其中 ,
,
即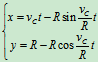 轨迹为摆线(可演示轮子运动时,
轨迹为摆线(可演示轮子运动时,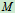 点的轨迹画出来)
点的轨迹画出来)
速度: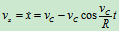

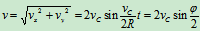

可知  (如图20)
(如图20)
当
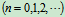 时,
时,
即 点接触地时
点接触地时  (此时可演示图20中轮子运动时
(此时可演示图20中轮子运动时 点速度变化情况)
点速度变化情况)
加速度: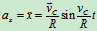

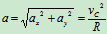
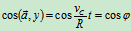
即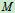 点的加速度大小为常量,方向恒指向轮心
点的加速度大小为常量,方向恒指向轮心




 浙公网安备 33010602011771号
浙公网安备 33010602011771号