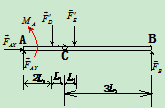
例 4:长凳的几何尺寸和重心位置如图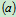 所示,设长凳上的重量为
所示,设长凳上的重量为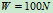 ,求重为
,求重为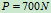 的人在长凳上的活动范围
的人在长凳上的活动范围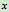 。
。
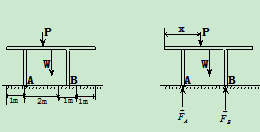
解:1、取研究对象:长凳
2、受力分析:如图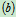 所示
所示
3、列平衡方程求解
长凳受平行力系作用,但有3个未知量: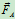 、
、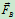 的大小和
的大小和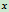 。需要利用翻倒条件补充一个方程。下面分两种情况讨论,当人在长凳的左端时,长凳有向左翻倒的趋势,要保证凳子平衡而不向左翻倒,需满足平衡方程
。需要利用翻倒条件补充一个方程。下面分两种情况讨论,当人在长凳的左端时,长凳有向左翻倒的趋势,要保证凳子平衡而不向左翻倒,需满足平衡方程
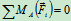
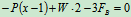
和限制条件 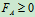
临界平衡时 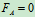
解得: 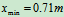
当人在长凳的右端时,长凳有向右翻倒的趋势,要保证凳子平衡而不向右翻倒,需满足平衡方程
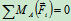
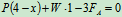
和限制条件 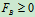
临界条件时 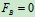
解得 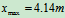
所以人在长凳上的活动范围为 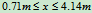
2、静定和静不定问题
- 静定和静不定问题概念。
前面例子所讨论的平衡问题,未知力的个数正好等于平衡方程的数目,因而能由平衡方程解出全部未知数。这类问题称为静定问题。相关的结构称为静定结构。工程上为了提高结构的强度常常在静定结构上再附加一个或几个约束,从而使未知约束力的个数大于独立平衡方程的树目。因而,仅仅由平衡方程无法求得全部未知约束力,这时的平衡问题称为超静定问题或静不定问题,相应的结构称为超静定结构或静不定结构。
- 平面内刚体的自由度
以 坐标平面内运动的刚体为例,说明平面内运动的刚体自由度。
坐标平面内运动的刚体为例,说明平面内运动的刚体自由度。
若刚体平移(平动),有两个自由度
若刚体定轴转动,有一个自由度。
若刚体作平面一般运动,(既有平动又有转动),有3个自由度 。
3)刚体的三种约束状态
所谓约束状态是指刚体在空间所收的限制状况。约束状态与自由度有关,自由度大于零称为不完全约束,自由度等于零者称为完全约束。
若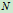 自由度
自由度 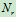 ——未知约束力个数
——未知约束力个数
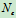 ——独立平衡方程数目
——独立平衡方程数目
则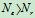 时,
时,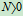 为不完全约束
为不完全约束
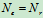 时
时 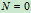 为完全约束,且为静定问题
为完全约束,且为静定问题
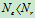 时
时 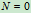 为完全约束,但为超静定问题
为完全约束,但为超静定问题
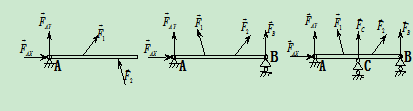
图 所示为不完全约束,图
所示为不完全约束,图 所示为完全约束,且为静定结构,图
所示为完全约束,且为静定结构,图 所示为完全约束,但为超静定结构。
所示为完全约束,但为超静定结构。
4)超静定次数
超静定问题中,未知约束力的个数与独立的平衡方程数目之差,称为超静定次数,与超静定次数对应的约束对于结构保持静定是多余的,故称为多余约束。
静不定次数用之表示由式确定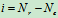
3.简单多刚体系统平衡问题
多刚体系统平衡问题的特点是:仅仅考虑系统的整体或某个局部(单个刚体或局部刚体系统)不能确定全部未知力。为了解决多刚体系统的平衡问题,需将平衡的概念加以扩展,即:系统若整体是平衡的,则组成系统的每一局部以及每一个刚体也必然是平衡的。如刚体系统由 个刚体组成,设其中
个刚体组成,设其中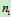 个刚体受平面力偶系作用,
个刚体受平面力偶系作用,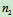 个刚体受平面汇交力系或平面平行力系作用,
个刚体受平面汇交力系或平面平行力系作用,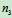 个刚体受平面力系作用,则
个刚体受平面力系作用,则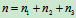 ,分别考虑每个刚体的平衡,总共可得
,分别考虑每个刚体的平衡,总共可得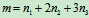 个独立的平衡方程。若未知的外约束力和内约束力的总数为
个独立的平衡方程。若未知的外约束力和内约束力的总数为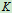 个,如
个,如 ,则刚体系统是静定的,否则是静不定的,静力学只研究静定平衡问题。
,则刚体系统是静定的,否则是静不定的,静力学只研究静定平衡问题。
例5图示起重机置于组合梁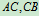 上,各梁的自重不计,已知:
上,各梁的自重不计,已知: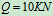 ,起吊重物
,起吊重物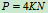 ,
,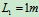 ,
,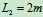 ,试求支座
,试求支座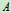 、
、 的约束力。(设梁与起重机光滑接触)
的约束力。(设梁与起重机光滑接触)
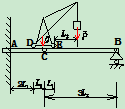
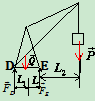
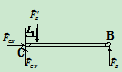
解:1、判断系统的静定性: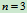 ,其中
,其中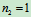 ,
,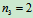 ,得
,得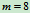 ,而
,而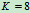 。所以静
。所以静
定。整体不单独静定,而起重机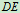 单独静定,故可以研究起重机
单独静定,故可以研究起重机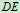 。
。
2、取研究对象:起重机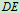
受力分析:如图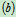
列方程求解:
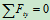
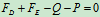
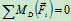
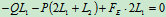
解得: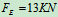 ,
,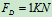
3、取研究对象: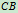 梁
梁
受力分析如图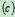
列方程求解: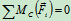
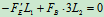
解得: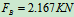
4、选择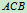 为研究对象,
为研究对象,
受力分析如图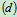
列方程求解:
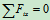
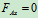
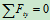
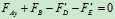
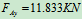
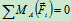
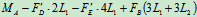 =0
=0
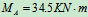
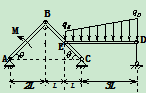
例6、在图示结构中,各杆自重不计,已知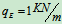 ,
,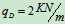 ,
, ,
,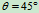 ,
,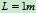 ,
,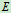 、
、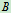 处为铰链联接,试求:
处为铰链联接,试求:
- 支座
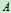 、
、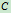 的约束反力
的约束反力
- 铰链
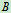 的约束反力
的约束反力
解:1、判断系统的静定性: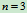 ,
,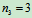 ,
,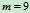 静定,
静定,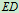 单独静定,所以应先研究
单独静定,所以应先研究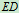 ,然后由于
,然后由于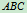 可列两个一元一次方程,所以接着应研究
可列两个一元一次方程,所以接着应研究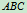 。
。
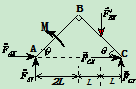
2,研究对象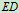 :
:
受力分析如图
列方程求解:
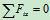
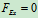
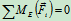
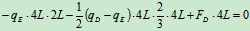

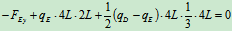
解得: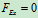
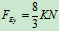
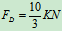
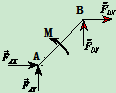
3、研究对象: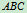
受力分析,如图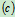
列方程求解:
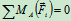
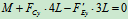

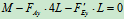
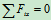
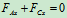
解得: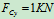
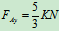
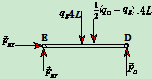
4、研究对象: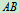
受力分析如图
列方程求解:
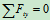
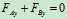
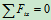
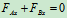
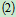
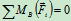

解得: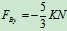 ,
,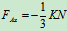 ,
,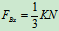 ,
,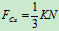
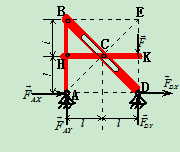
例7、不计自重的三杆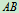 ,
,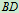 ,
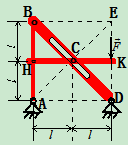
,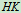 用铰链、滑槽、销钉连成如图14.18
用铰链、滑槽、销钉连成如图14.18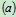 所示结构,图中
所示结构,图中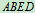 围成正方形,
围成正方形,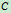 为正方形中心点,
为正方形中心点,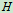 为
为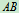 杆中点,水平杆
杆中点,水平杆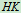 的
的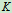 端受铅直向下的力
端受铅直向下的力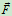 作用。固定在水平杆
作用。固定在水平杆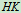 中点的销钉与滑槽光滑接触,试求各约束处的约束力。
中点的销钉与滑槽光滑接触,试求各约束处的约束力。
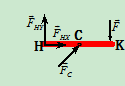
解:1.判断系统的静定性: 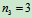 ,
,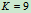 ,
,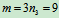 ,所以系统试静定的。系统整体的约束力数4,不单独静定,但有两个一元一次方程,故仍可先研究整体
,所以系统试静定的。系统整体的约束力数4,不单独静定,但有两个一元一次方程,故仍可先研究整体
2.取研究对象:整体:
分析受力:如图
列平衡方程求解:
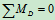
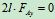
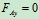
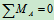
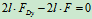

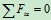
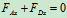
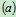
3.取研究对象:杆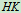
分析受力:如图
列平衡方程求解:
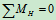
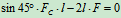
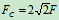
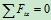
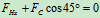
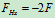
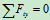
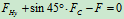
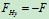
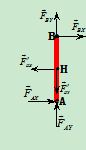
4.取研究对象:杆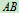
分析受力:如图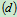
列方程求解:
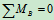
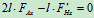
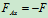

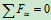
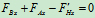
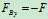
将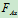 的值代入
的值代入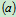 中,得:
中,得: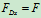
例8.无重直杆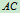 长
长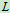 ,
,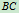 长
长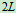 ,
,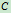 端用铰链相连,
端用铰链相连,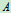 、
、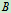 两端用铰链固定。两杆各与铅垂线的夹角
两端用铰链固定。两杆各与铅垂线的夹角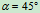 ,
,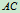 杆中点
杆中点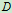 作用铅垂力
作用铅垂力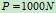 ,
,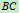 杆中点
杆中点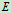 作用水平力
作用水平力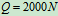 ,试求
,试求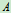 、
、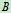 两处之约束力。
两处之约束力。
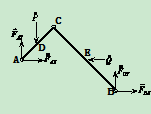
解:1.判断系统的静定性: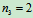 ,
,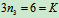 ,所以静定,但没有单独静定的物体,也无一元平衡方程,需解联元方程组
,所以静定,但没有单独静定的物体,也无一元平衡方程,需解联元方程组
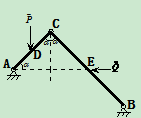
2.取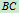 为研究对象
为研究对象
受力分析
列方程:
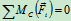
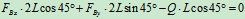
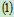
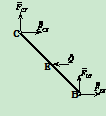
3.整体为研究对象
受力分析
列方程:
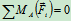
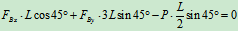
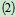
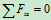
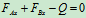
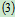
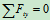
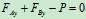
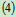
联立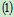 ,
,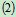 可得:
可得: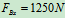 ,
,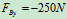
代入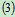 ,
, 得:
得: 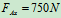 ,
,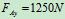
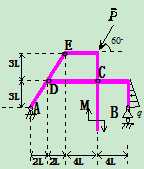
例9.图示结构由曲杆 ,
,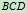 及直杆
及直杆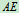 铰链组成,各杆自重不计。已知:
铰链组成,各杆自重不计。已知: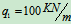 ,
,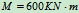 ,
,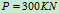 ,
,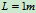 试求:曲杆
试求:曲杆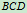 在铰链
在铰链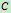 、
、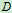 处所受的力
处所受的力
解:1.判断系统的静定性: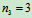 ,
,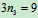 ,
,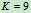 静定
静定
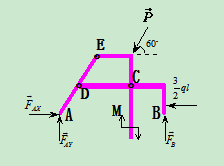
2.研究对象整体:
受力分析:如图14.20 所示
所示
列方程:
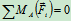
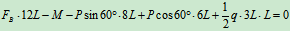
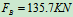
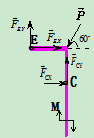
3.研究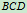 杆
杆
受力分析:如图4.20 所示
所示
列方程:
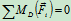
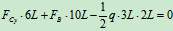
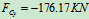
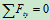
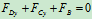
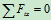
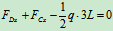
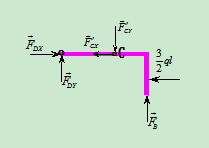
4.研究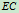
受力分析:如图4.20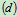 所示
所示
列方程:
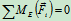
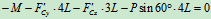
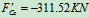
代入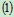 式可得:
式可得: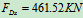
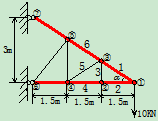
例10.图示一平面桁架,试求3、4、5、6杆的内力
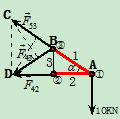
解前说明:
桁架:由一些直杆两端铆接、焊接或榫接而成具有坚固性的杆架结构。若所有杆件的中心线都在一个平面内,称为平面桁架。
节点: 桁架中各杆的连接点。
桁架内力计算的假定:
- 直杆两端都为光滑铰链连接。
- 杆件自重不计。
- 架所受的外载荷都作用在节点上,其作用线在桁架平面内。
求解静定 架中各杆件的内力一般采用节点法截面法,下面把这两种方法分别给以说明。
解法一(节点法)
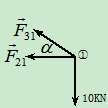
- 取研究对象:节点
受力分析:如图4.21
列方程求解:
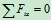
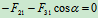
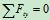
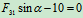
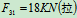 ,
,
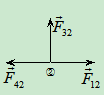
- 取研究对象:节点
受力分析:如图4.21
列方程求解:
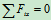
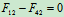
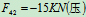
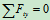
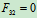
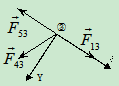
3.取研究对象:节点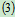
受力分析:如图4.21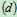
列方程求解:
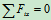
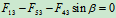
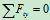
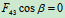
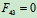 ,
,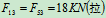
解法二(截面法)
- 用截面将 4、5、6杆截断,取其右半部分为研究对象
- 受力分析:如图4.21
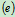 ,其中是零力杆:即
,其中是零力杆:即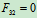
- 列方程求解:
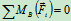
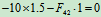
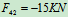
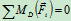
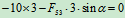
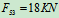
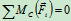
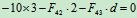
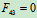
求零力杆的方法:
- 三杆铰接无外载
- 两杆铰接无外载
- 两杆铰接有外载,其中一杆与外载共线




 浙公网安备 33010602011771号
浙公网安备 33010602011771号