- 矩阵的秩
定义4 在m´n矩阵A中, 任取k行与k列(k£m, k£n), 位于这些行列交叉处的k2个元素, 不改变它们在A中所处的位置次序而得的k阶行列式, 称为矩阵A的k阶子式.
m´n矩阵A的k阶子式有
个。
当A的所有元素都是零时，A的任何子式都必然是零；当A中有一个元素不为零时，A中至少有一个一阶子式非零，再看A的所有二阶子式，如果有非零的子式，再看A的所有3阶子式，这样下去，如果A至少有一个非零的r阶子式，而A的所有r+1阶子式都是零，也就是A的最高阶非零子式的阶数为r，r揭示了矩阵A的内在特性。
定义5 在m´n矩阵A 中，若非零子式的最高阶数为r，数r称为矩阵A的秩数, 记作R(A)=r 。
如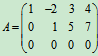
，A中有非零的2阶子式，但它所有的3阶子式全为零，故R(A)=2。
由秩数的定义可得下面结论：
（1）若A是零矩阵，则R（A）=0
（2）若A是m´n阶非零矩阵，则1≤R（A）≤min(m，n)。
注意：矩阵A的秩数不可能大于其行数或列数。
特别地，
R（A）=m，称A为行满秩矩阵；
R（A）=n，称A为列满秩矩阵；
当A是n阶方阵，又R（A）=n，称A为满秩矩阵。
可见，单位矩阵是满秩矩阵。
（3）对于行阶梯矩阵，其非零行的行数就是该矩阵的秩数。如
，R(A)=2
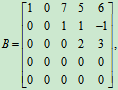R(B)=3
定理4 若矩阵A和B等价，则R(A)= R(B)
由定理4，我们得到如下求矩阵秩数的方法：先利用初等行变换将矩阵A化为行阶梯矩阵B，再根据B的秩数等于其非零行的行数，即求得R（B），又因为A～B，所以R（A）=R（B）。
例5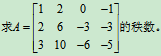 
解：对矩阵A实施初等行变换
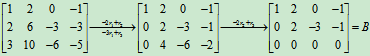
B是行阶梯矩阵，其非零行数为2，所以R（B）=2。
再由定理4得，R（A）=R（B）=2
例6 证明：A为任意矩阵，用可逆矩阵P左乘A，则R（PA）=R（A）。
证明：因为P是可逆矩阵，根据定理3知，P恒为若干个初等矩阵之积。设
Ｐ＝Ｊs…Ｊ1 ， Ｊ１，…Ｊs为初等方阵
又
ＰＡ＝Ｊs…Ｊ1 Ａ
上式表明，Ａ经过若干次初等变换变成ＰＡ，所以Ａ～ＰＡ，则R（PA）=R（A）。
