第一节 初等变换
定义1 下面三种对矩阵的变换，统称为矩阵的初等行变换
(1)互换矩阵中两行的位置如果第i, j两行互换，记作ri«rj;
(2)以任意数k¹0去乘矩阵的第i行所有元素，记作k ri);
(3)把矩阵的第i行的k倍加到第j行上去（其中k 为任意数），记作krirj,).
例1 设矩阵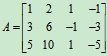
，对A施以行初等变换。
解：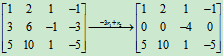
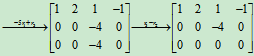
从例1知，矩阵A经过初等行变换化成矩阵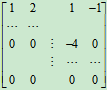
我们称这种类型的矩阵为行阶梯矩阵。其特点为：每一行首位非零元素所在列的位置逐个增加，且零行在非零行下面。如
都是行阶梯矩阵。而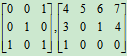
是非行阶梯矩阵。
如果对例1中的行阶梯矩阵进一步实施行变换，可使它更加简化。
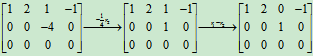
最后这个矩阵称为行最简型矩阵，其特点是：
（1）满足行阶梯矩阵特征，是一个行阶梯矩阵
（2）它每行中首位非零元素是1，而且首位非零元素所在列除1外，其它元素都是0，如：
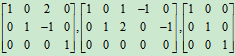
都是行最简型矩阵。
对于矩阵的初等变换有如下几点说明：
（1）初等行变换可以将任意m×n 阶矩阵化为行阶梯矩阵和行最简型矩阵。
（2）初等行变换后的矩阵一般情况下与原矩阵不相等，所以一定要用"→"来连接变换前后的矩阵。
（3）三种初等行变换都是可逆的，即经变换后的矩阵再施以同类型的变换又会回到原矩阵。如
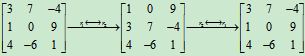
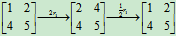
注: 三种变换都是可逆的, 且其逆变换是同一类型的初等变换; 变换ri«rj的逆变换就是其本身; 变换ri´k的逆变换为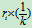
(或记作ri¸k); 变换rikrj的逆变换为ri(-k)rj(或记作ri-krj).
（4）如果对行的三种变换换成对列的，同样得到对列的三种变换，分别记为ci«cj（对调i, j两列）；k ci（以任意数k¹0去乘矩阵的第i列的所有元素）；kci cj （第i列的k倍再加到第j列上）。这就是矩阵的初等列变换。矩阵的初等行变换和初等列变换统称为矩阵的初等变换。
定义2 如果矩阵A经有限次初等变换变成矩阵B, 就称矩阵A与B等价, 记作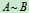
.
如果An是可逆矩阵，那么An经过有限次的初等变换可化成单位矩阵En，所以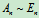
，等价矩阵具有下列性质:
(i)反身性 A~A;
(ii)对称性 若A~B, 则B~A;
(iii)传递性 若A~B, B~C, 则A~C .
例2 将矩阵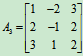
化为行最简型矩阵
解
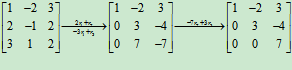
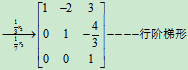
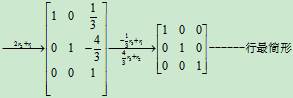
所以
