矩阵论基础 2.4 矩阵的分块法

第四节 矩阵的分块法

 

在进行矩阵的运算时，如果矩阵很大，作各种矩阵运算时会很烦琐，可以采用将矩阵分块的方法，用一系列水平与垂直的直线将矩阵A分成若干个小矩阵，每个小矩阵称为A的子块，以子块为元素的形式上的矩阵称为分块矩阵，对分块后的矩阵进行运算，会大大减少运算量，简化计算过程，这种方法称为矩阵的分块法。

例如，

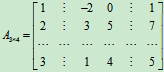
用矩形中所画水平和垂直直线分成6块，记为

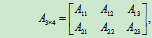
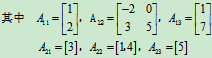
在形式上矩阵A原为3×4阶矩阵，分块后，A用子块表示为2×3阶矩阵。

显然，对给定的矩阵有多种分块法，例如：将矩阵

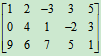
分成2行2列的分块矩阵，可采用下列分块法：

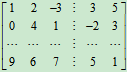
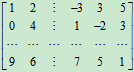
共有8种分法。

一般地，要按照问题的具体需要对矩阵进行合理分块，下面介绍几种特殊的分块方法：

（1）按行分块：将矩阵的每一行作为一个子块，记为

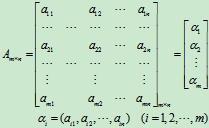
这种分法将m×n阶矩阵化为m元列矩阵。

（2）按列分块：将矩阵的每一列作为一个子块，记为

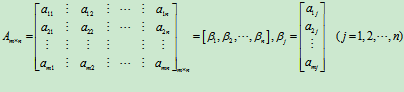
这种分法将m×n阶矩阵化为n元行矩阵。

（3）对角矩阵：对于n阶方阵A_n，如果将其化为只有在主对角线上有非零子块，且均为方阵，其余子块都为零矩阵，即

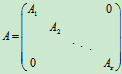
其中A_i是非零方阵，（i=1,2,…,r），称A为分块对角矩阵。

这种分块法可简化复杂的方阵运算。分块对角矩阵A有下列性质：

（1） |A|=|A₁||A₂|× × ×|A_r|.

（2）如果|A_i|¹0(i=1, 2, × × ×r), 则|A|¹0, 并有

.

例16 设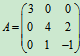, 求A^-1.

解 ,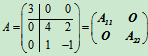

A₁₁=(3), ;

, ;

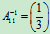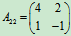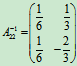所以 .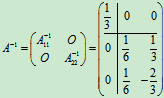

分块矩阵的运算和一般矩阵的运算定义一样，所不同的是一般矩阵的运算是在元素与元素之间进行，而分块矩阵的运算是在子块与子块之间进行。

设矩阵A与B为同型矩阵，且对A，B采用相同的分块法, 有

, ,

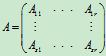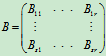其中A_ij与B_ij同型（i=1,2,…,s;j=1,2,…,r) 那么

（1） .

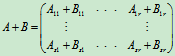(2) .

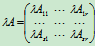（3）

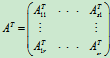
(4)设U为m´p矩阵, V为p´n矩阵, U和V分块成

, ,

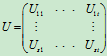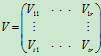其中U_i1, U_i2, × × ×, U_it的列数分别等于V_1j, V_2j, × × ×, V_tj,的行数, 那么

,

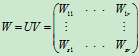其中 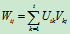(i=1, 2, × × ×, s; j=1, 2, × × ×, r).

例17 设A，B为n 阶可逆方阵，证明分块矩阵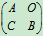也可逆。且

.

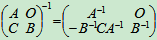证明：A，B为n 阶可逆方阵，由可逆矩阵存在的充分必要条件，可得|A|≠0，|B|≠0，有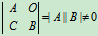

所以 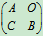是可逆的。

设

,

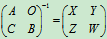则

.

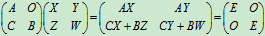由此得 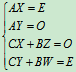Þ,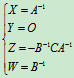

所以 .
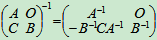