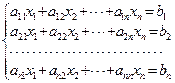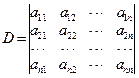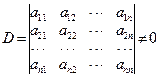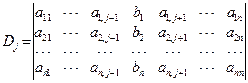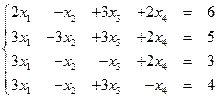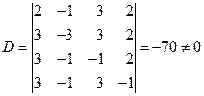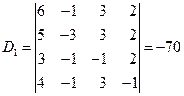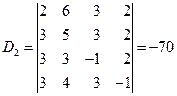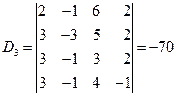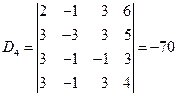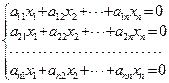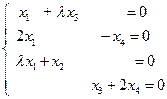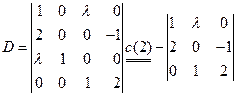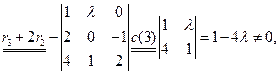第五节 Cramer定理
设含有n 个未知量的n个线性方程构成的线性方程组为
由未知数的系数组成的n阶行列式
称为n元线性方程组(Ⅰ)的系数行列式.
定理3 (Cramer定理) 如果线性方程组(Ⅰ)的系数行列式不等于零, 即
那么, 方程组(Ⅰ)有唯一解,且解可用行列式表示为
其中D j (j=1, 2, × × × , n)是把系数行列式D中第j列的元素a1j, a2j, × × × , anj对应地换为方程组的常数项b1, b2, × × × , bn后所得到的n阶行列式, 即
注意:Cramer定理中,
(1)D≠0;
(2)解是唯一的;
因此,求解线性方程组(Ⅰ)时,先求系数行列式D,当D≠0时,再求另外n个行列式Dj(j=1,2,…,n),然后便给出方程组(Ⅰ)的唯一解。
例17 求解线性方程组
解
于是得
Cramer定理的逆否命题为:
定理4 线性方程组(Ⅰ)无解或解不唯一,则其系数行列式D=0
当线性方程组(Ⅰ)的常数项b1=b2=× × × =bn=0时, 线性方程组(Ⅰ) 为
叫做n元齐次线性方程组。相应地,线性方程组(Ⅰ)右端的常数项b1, b2, × × × , bn不全为零时,线性方程组(Ⅰ)叫做n元非齐次线性方程组。
定理5 如果齐次线性方程组(Ⅱ)的系数行列式D¹0, 则齐次线性方程组(Ⅱ)只有零解(没有非零解)。
注意:线性方程组(Ⅱ)无论D是否为零,都有零解(解全为零),但D¹0时,只有唯一零解;D=0时,除零解外,还有其它的解,这个问题以后还会讨论。
例18 设齐次线性方程组
只有零解,求λ的值。