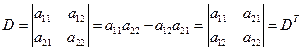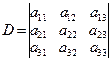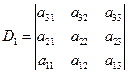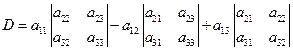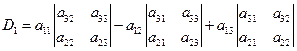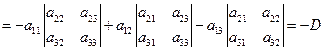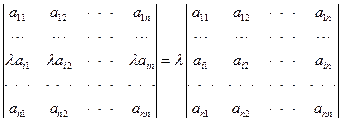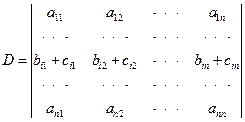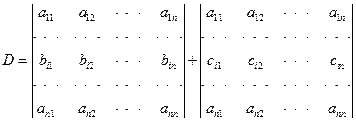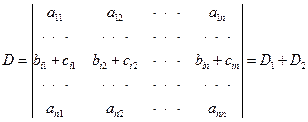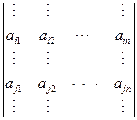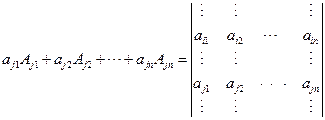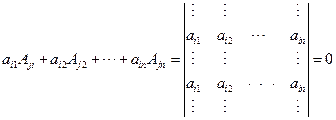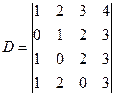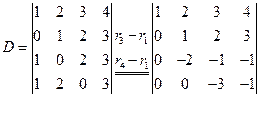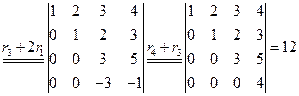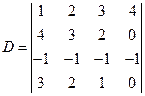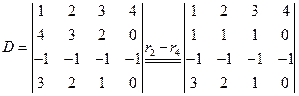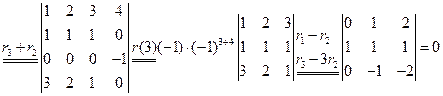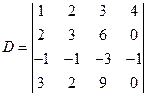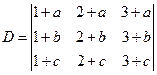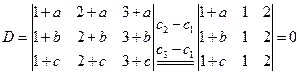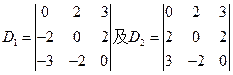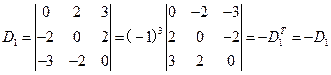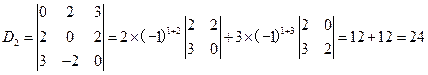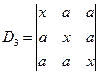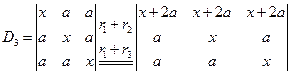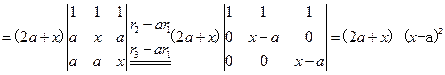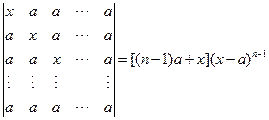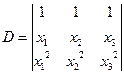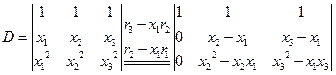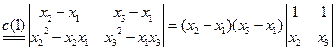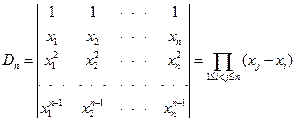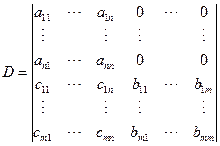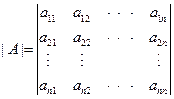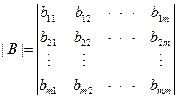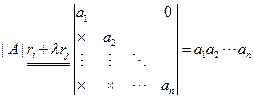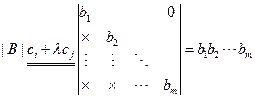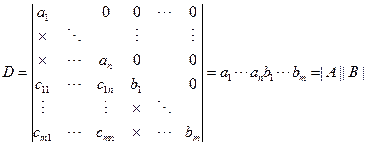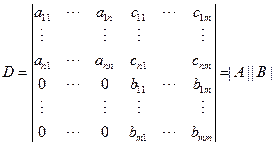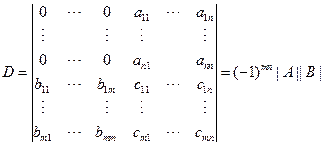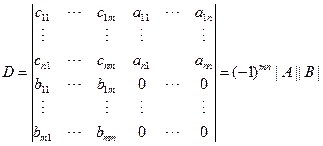第四节 行列式的性质
行列式有如下7条性质
n阶行列式:
注意:转置行列式也可以看作以主对角线为轴,行列式翻转180°的结果.
性质1 行列式D=DT
应用数学归纳法,当n=2时,结论显然成立,即
假设n-1时结论成立,即n-1阶行列式与它的转置行列式相等,将n阶行列式D按第一行展开,有![]()
将n阶行列式DT按第一列展开,有
所以n阶行列式D=DT
由行列式的性质1可以看出,行列式的行和列的地位相同,行所具有的性质对于列也成立,反之亦然.
性质2 若行列式中有某一行(或列)为零,则这个行列式的值等于零.
说明:把行列式按此行(或列)展开即可.
性质3 行列式中任何两行(或两列)互换位置, 行列式的值变号.
此性质对于n阶行列式也成立.
推论: 如果行列式有两行(列)完全相同, 则此行列式等于零.
说明:交换这两行(列)行列式D化为D1,由性质2知,-D=D1,由于交换的两行(列)相同,故
D=D1,因此,-D=D,D=0
性质4 行列式的某一行(列)中所有的元素都乘以同一数λ, 等于用数λ乘此行列式.反之, 行列式的某一行(列)中所有的元素有公因数,则可以把这个公因数从行列式中提出来,即
说明:上面两个行列式若按第i行展开,结果是相同的.
推论:行列式中如果有两行(列)元素对应成比例, 则此行列式等于零.
性质5 若行列式的某一行(列)的每个元素都是两个数之和, 例如第i行的元素都是两数之和: ![]() 即
即
则D等于下列两个行列式之和:
说明:记三个行列式为D,D1,D2,则
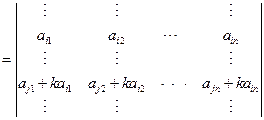
性质6 把行列式的某一行(列)的各元素乘以同一数然后加到另一行(列)对应的元素上去, 行列式不变. 即
说明:性质5和性质4可得性质6,这个性质在行列式的计算中非常重要.
性质7 行列式每一行(或列)的每个元素与另一行(或列)对应元素的代数余子式的乘积的和等于零,即
说明: n阶行列式按第j行展开,
在处理和计算行列式时,常用上述7条性质,为了表达简洁,引入下列记号
解:利用行列式的性质,把D化为相等的上(下)三角行列式,再写出结果,这是计算行列式的常用方法.
说明:
(1)利用性质6,先把a11下面的所有元素化为零;
(2) 再把a22下面的所有元素化为零;
(3)重复操作,直到化为三角行列式为止;
(4)对于列也可以采用同样的处理方法,化为其它类型的三角行列式,再求值.
求行列式的值时,常用的方法还有按某行(列)展开,达到降阶的目的,从而化简行列式,直到求出结果为止.
要善于用两种方法求行列式的值:
1.化为三角行列式(四种结果)
2.按某一行(列)展开(选零较多的行(列)).
解:因第一列与第三列对应元素成比例,所以D=0.
解:D1中每行提出公因子(-1),得
所以D1=0
D2按第一行展开,得
同理可得n阶Vandermonde行列式
对|A|作若干次ri+λrj操作,化为下三角行列式,设为
对|B|作若干次ci+λcj操作,化为下三角行列式,设为
把对|A|的操作全部施于D的前n行,再把对|B|的操作全部施于D的后m列,得
同理可知以下三个零块行列式的值
说明:1.(2)中行列式D可化为下三角行列式,利用前面的结论,可推得
2. 四种结果要牢记.


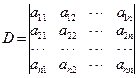
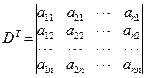
![clip_image002[1] clip_image002[1]](https://images.cnblogs.com/cnblogs_com/begtostudy/WindowsLiveWriter/1.4_B1F6/clip_image002%5B1%5D_thumb.gif)
![clip_image004[1] clip_image004[1]](https://images.cnblogs.com/cnblogs_com/begtostudy/WindowsLiveWriter/1.4_B1F6/clip_image004%5B1%5D_thumb.gif)