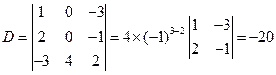第二节 行列式按行展开
计算三阶行列式时有如下规律:
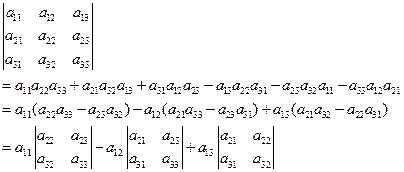
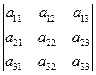 ,
,![clip_image004[1] clip_image004[1]](https://images.cnblogs.com/cnblogs_com/begtostudy/WindowsLiveWriter/1.2_B01E/clip_image004%5B1%5D_thumb.gif) ,
,![clip_image004[2] clip_image004[2]](https://images.cnblogs.com/cnblogs_com/begtostudy/WindowsLiveWriter/1.2_B01E/clip_image004%5B2%5D_thumb.gif)
把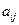 所在的行和列都划掉,剩下的元素保持原来的相对位置不变而构成的新行列式称为元素
所在的行和列都划掉,剩下的元素保持原来的相对位置不变而构成的新行列式称为元素![clip_image008[1] clip_image008[1]](https://images.cnblogs.com/cnblogs_com/begtostudy/WindowsLiveWriter/1.2_B01E/clip_image008%5B1%5D_thumb.gif) 的余子式,记作
的余子式,记作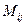 。
。
记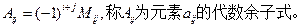
上述三阶行列式可记为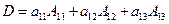
即,三阶行列式等于它的第一行的每个元素与其对应代数余子式的乘积之和。
如果定义一阶行列式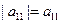 ,则上述展开规律同样适用于二阶行列式,即
,则上述展开规律同样适用于二阶行列式,即
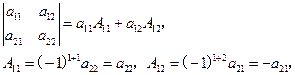
例3 按第一行展开计算行列式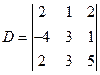
解
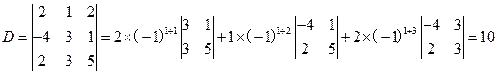
行列式按第一行展开规律还可以类推为如下定理:
定理1 三阶行列式等于它的任一行(或列)的每个元素与它对应的代数余子式的乘积之和即 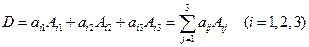
或 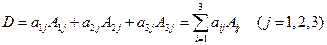
例如,例3中的行列式按第二行展开为
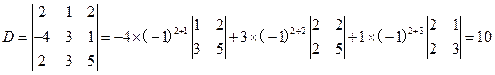
按第三列展开为
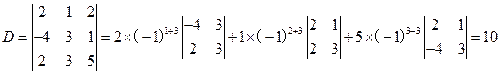
例4 计算行列式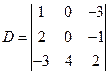
解 第二列有两个元素为零,按第二列展开较好