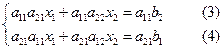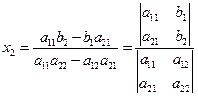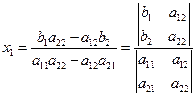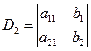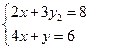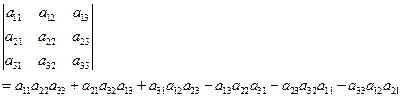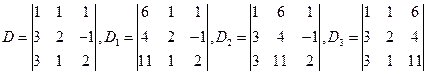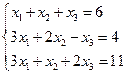第一节 二阶和三阶行列式
在介绍行列式概念之前,我们先构造一个数学玩具:把4个数放在一个正方形的四个角上,在加上两条竖线,即![]() ,规定这个玩具对应于一个结果:两个对角线上的数的乘积之差。即
,规定这个玩具对应于一个结果:两个对角线上的数的乘积之差。即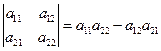
![]() 所在方向的对角线称为主对角线,
所在方向的对角线称为主对角线,![]() 所在方向的对角线称为副对角线。
所在方向的对角线称为副对角线。
定义1 4个数![]() 称
称![clip_image004[1] clip_image004[1]](https://images.cnblogs.com/cnblogs_com/begtostudy/WindowsLiveWriter/1.1_AEAF/clip_image004%5B1%5D_thumb.gif) 为一个二阶行列式;
为一个二阶行列式;![]() 所在的行称为第一行,记为
所在的行称为第一行,记为![]() (r来源于英文row),
(r来源于英文row),![]() 所在的列称为第二列,记为
所在的列称为第二列,记为![]() (c来源于英文column),因其共有两行两列,所以称为二阶行列式,
(c来源于英文column),因其共有两行两列,所以称为二阶行列式,![]() 是第二行第一列的元素。
是第二行第一列的元素。
可叙述为:二阶行列式的对应值等于主对角线上两元素之积减去的副对角线上二元素之积所得的差, 这一计算法则称为对角线法则.
此玩具的用途在于:
用消元法,先消去![]() 所在的项,方程(2)´a11,方程(1)´a21得
所在的项,方程(2)´a11,方程(1)´a21得
此规律被称为Cramer定理。
同理类推,用对角线法则可以定义3阶行列式如下:
例2 计算3阶行列式
解:D=1×2×2+3×1×1+3×1×(-1)-1×2×3-(-1)×1×1-2×1×3=-7
D1=6×2×2+4×1×1+11×1×(-1)-1×2×11-(-1)×1×6-2×1×4=-7
D2=1×4×2+3×11×1+3×6×(-1)-1×4×3-(-1)×11×1-2×6×3=-14
D3=1×2×11+3×1×6+3×1×4-6×2×3-4×1×1-11×1×3=--21
实际上,D,D1,D2,D3来自线性方程组



![clip_image004[2] clip_image004[2]](https://images.cnblogs.com/cnblogs_com/begtostudy/WindowsLiveWriter/1.1_AEAF/clip_image004%5B2%5D_thumb.gif)