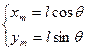教学目标:
1. 对约束方程、广义坐标、自由度、理想约束和虚位移有清晰的概念,并会计算虚位移。
2. 能正确地运用虚位移原理求解物体系的平衡问题。
3. 对广义力和广义坐标形式的虚位移有初步的理解,并会计算广义力。
本章重点:
虚位移、理想约束的概念,应用虚位移原理求解物体系的平衡问题。
本章难点:
广义力的概念,广义坐标形式的虚位移原理。
教学过程:
引言:本章研究平衡问题,用功的概念求解,称为分析静力学
一、约束 约束方程
1.约束:事先对物体的运动所加的限制条件
2.约束方程:用来表示约束的数学方程。如图15。1所示
图15.1(b)所示为曲柄连杆机构
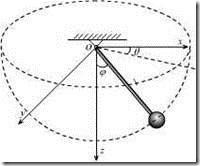
图15(d)所示为摆长![]() 随时间变化的单摆,设摆长开始时
随时间变化的单摆,设摆长开始时![]() ,然后以不变速度
,然后以不变速度![]() 拉动细绳的另一端。
拉动细绳的另一端。
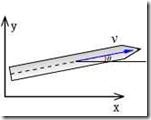
图15(e)所示为冰刀在平面上的运动,冰刀中心速度只能沿冰刃方向。
3.约束分类
1)几何约束
运动约束
2)稳定约束
非稳定约束
3)双面约束
单面约束
二.自由度和广义坐标
自由度:在完整约束系统中,自由度是确定系数位置的独立坐标数。
广义坐标:确定质点系位置的任意独立变量
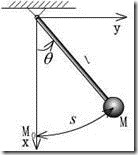
如:单摆在平面中摆动(图15.2)
单摆的约束方程为:
一般情况下,质点系中任意质点![]() 的矢径和直角坐标与广义坐标的函数关系为
的矢径和直角坐标与广义坐标的函数关系为
三.虚位移:某瞬时,质点(质点系)为约束所许可的任何无限小位移,称为质点(质点系)的虚位移。通常用![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,表示
,表示
虚位移与实位移的区别
实位移:![]() ,是
,是![]() 时间内的位移,与质点受力和初始条件有关,约束允许有确定的方向(唯一性),实位移用微分符号“
时间内的位移,与质点受力和初始条件有关,约束允许有确定的方向(唯一性),实位移用微分符号“![]() ”
”
虚位移:![]() ,无限小量,约束允许,可以有多种不同的方向(有多个),是一个纯粹的几何量。虚位移用变分符号“
,无限小量,约束允许,可以有多种不同的方向(有多个),是一个纯粹的几何量。虚位移用变分符号“![]() ”
”
虚位移与实位移的联系:
在稳定的几何约束下,无限小的实位移就不是虚位移之一。如位于气球上的质点m,设气球正在膨胀其半径变化规律为:![]() ,M点虚位移:令
,M点虚位移:令![]() ,
,![]() 在过M点的切平面内;M点实位移
在过M点的切平面内;M点实位移
各点虚位移关系计算:
1)几何法(求速度的几何法)
2)解析法(写坐标进行变分运算)
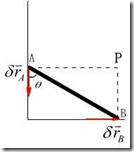
例15.1 已知:在图15。4(a)中,设![]() ,求
,求![]() 时,AB两点虚位移关系。
时,AB两点虚位移关系。
解:
1)几何法。由图示位置,任给系统一组虚位移(图15.4)
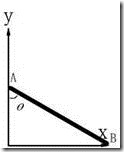
2)解析法:建立坐标如图15.4(b)所示
四.理想约束
若质点系在虚位移的过程中,约束力的虚功之和为零,则此类约束称为理想约束。
五.虚位移原理(虚功原理)
具有双面、稳定、理想约束的质点系,在给定位置平衡的必要与充分条件是:所有作用于质点系的主动力在质点的任何虚位移中的虚功之和等于零,表示为
该式又称为静力学普遍方程。
设质点系处于平衡,其中任一质点![]() 也处于平衡,设
也处于平衡,设![]() 和
和![]() 分别为作用在此质点上的主动力、约束力,有
分别为作用在此质点上的主动力、约束力,有
将以上这些等式相加,有
若质点系具有理想约束,可得
采用反证法。假设式![]() 成立,而质点系不处于平衡状态,那么至少有一个质点将从静止进入运动,质点系的动能T必增加,同时质点系必然发生实位移
成立,而质点系不处于平衡状态,那么至少有一个质点将从静止进入运动,质点系的动能T必增加,同时质点系必然发生实位移![]() ,根据质点系动能定理有
,根据质点系动能定理有
在稳定约束的条件下,实位移是虚位移中之一,因此存在某一虚位移![]() ,等于实位移,在理想约束条件下,有
,等于实位移,在理想约束条件下,有![]() ,于是可得出
,于是可得出
这个结论与原假设矛盾,故质点系处于平衡。