Matrix and linear algebra in F#, Part III: Eigen decomposition and face recognition[z]

 

The theory

Face recognition is one of the most import research problems in computer vision. It is also an important application for everyday use. A lot of security system has a face recognition component, as well as other parts, e.g., finger print recognition.

While this application has a lot of algorithms, the most famous one must be Eigen face proposed in

M. Turk and A. Pentland (1991). "Eigenfaces for recognition". Journal of Cognitive Neuroscience 3 (1): 71–86.

The theory of Eigen face is very simple if one has learned the concept of Principal Component Analysis (PCA). Given a set of faces, each face is a n-by-m matrix, if we reshape the matrix into a vector, then each face can be viewed as a point in the (n*m) dimensional space. The idea of Eigen face is to find some directions, which are orthogonal, in this space such that the points(faces) have a minimal representation, or have maximum variance along these directions. As you can see, this is an optimization problem. The magic part is that this optimization is solved by Singular Value Decomposition (SVD).

The following is a summary of the procedures to get the eigen faces:

1. for a set of faces, F = {f1,…,fn}, calculate its mean face m. F is a d-by-n matrix, where d is the number of pixels of an face and n is the number of faces in the dataset. fi is a column vector.

2. subtract the mean face from F, get A = {f1-m, … fn-m}. We want to get the eigenvalues and eigenvectors of Cov(A) = A * A’. The eigenvectors associated with big eigenvalues are eigenfaces. (In the program part, we will visualize these eigenfaces).

However, Cov(A) is usually too big. (If there are 10K pixels in each face, then the size of Cov(A) would be 10K-by-10K). A trick is to calculate the eigenvalues and eigenvectors of A’ * A (which is of small size if the number of faces n is small.) and calculate Cov(A)’s based on them. This trick is well documented in the program section.

Once we get the Eigen faces, we can do face recognition. As said before, each eigen face is actually an direction, we can map our new face and the face in the database into the space defined by the set of Eigen faces. For example, if we have 10 Eigen faces, and we know that they are orthogonal to each other, thus a 10-D real space is defined by the 10 Eigen faces. Once real faces are mapped into this 10-D space, we can measure the distance between the new face and the existing faces, and find the closet one as the label face for the new face.

Here are some reference for interested readers:

1. Eigenface wiki page. It has the mathematics and links to programs and papers.

2. A Matab Tutorial. and this one. These two are very good tutorials using Matlab.

3. Principal Component Analysis (PCA), Singular Value Decomposition and Eigendecompsition. If you want to know more theory of it, you can move on to have a good understanding of PCA.

The ORL face dataset

There are more than 10 face datasets available online, which range from different complexity. I use an quite old one the ORL face dataset. This one is well pre-processed, e.g. under the same light condition, of the same size, etc.

Using this dataset greatly eases our work in processing the images and enables us to focus on the Eigen face algorithm in F#.

This dataset contains 400 faces from 40 subjects, with each having 10 faces. The images are of .PGM format. For the I/O of the images, I wrote a separate blog post on reading, writing and visualizing this image format. That post also features on how to write a simple GUI in F#.

The data structures for the dataset:

type pgm = matrix
type person = matrix array
type dataset = person array

Each PGM image is an F# matrix, each person is an array of matrices, and the dataset is an array of persons.

Then we define functions to read the dataset for a given folder:

let readPerson folder =
  seq {
      for i=1 to 10 do  
          let name = folder + string(i) + ".pgm"
          yield readPgm name
  } |> Seq.toArray

let readDataset folder =
  seq {
      for i=1 to 40 do
          let name = folder + "s" + string(i) + "\\"
          yield readPerson name
  } |> Seq.toArray

We also define functions to split the dataset into training data and testing data. Training data are used to get the eigenfaces, and then faces in the testing data are recognized using the eigenfaces. For each person, the first 7 faces are used for training, and the 3 left ones are used for testing.

let splitDataSet (ds:dataset) =
  let train = seq {
      for p in ds do
          yield (
              seq {
              for i=0 to 9 do
                  if i<7 then yield p.[i]
              } |> Seq.toArray )
      }
    
  let test = seq {
      for p in ds do
          yield (
              seq {
              for i=0 to 9 do
                  if i>=7 then yield p.[i]
              } |> Seq.toArray )
      }
  train |> Seq.toArray, test |> Seq.toArray

let strip (data: 'a array array) =
  let dat = seq {
      for x in data do
          for y in x do
              yield y
      }
  let label = seq {
      let i = ref 0
      for x in data do
          for y in x do
              yield !i
          i := !i + 1
      }
  dat |> Seq.toArray, label |> Seq.toArray

Function strip is used to transform a data set (matrix array array) into a flat array (matrix array) and remember their labels.

 

The program

First we write some help functions:

let mat2vec (A:matrix) =
  let n = A.NumRows
  let m = A.NumCols
  Vector.init (n*m) (fun i->A.[i%n, i/n])

let vec2mat (vec:vector) nrow ncol =
  if vec.Length <> nrow * ncol then failwith "vec length != nrow * ncol "
  Matrix.init nrow ncol (fun i j -> vec.[j*nrow+i])

let colSum (m:matrix) =
  let nrow = m.NumRows
  Matrix.foldByRow (fun a b -> a+b) (Vector.create nrow 0.0) m

let colMean (m:matrix) =
  let ncol = m.NumCols
  colSum m * (1.0 / float ncol)

mat2vec is concate the columns of a matrix into a long column vector, while vec2mat does the inverse. Their behaviors are similar to the reshape function in Matlab. colSum and colMean are similar to sum and mean in Matlab.

To use the eigen decomposition for a symmetric matrix, we call lapack via math-provider. Read Part II of this F# matrix series to know to how use them.

open Microsoft.FSharp.Math

open Microsoft.FSharp.Math.Experimental
let isSucc = Experimental.LinearAlgebra.Lapack.Start()
printfn "service = %A" (if isSucc then "Netlib lapack" else "Managed code")
let eig = LinearAlgebra.EigenSpectrumWhenSymmetric

eig is a shorthand for EigenSpectrumWhenSymmetric. Notice that eig gets the eigenvectors in a matrix, each row of which is an eigenvector. This may be a bug in the math-provider wrapper, but since it only deals with square and symmetric matrices, this incontinence does not hurt too much.

The main function:

let eigCov (faces:matrix) numVecs =

    // each column is a face

  let nrow = faces.NumRows
  let ncol = faces.NumCols
  let colm = colMean faces
  let A = Matrix.init nrow ncol (fun i j -> faces.[i,j] - colm.[i])
  // A - each column is a difference face
  // Cov(A) = A * A', a big matrix
  // trick: A'*A*v(i) = lambda(i)*v(i)
  //      A*A'*A*u(i) = lambda(i)*A*u(i)
  //      (A*u(i)) is an eignvector of Cov(A)
  // L(A) = A' * A
  let L = A.Transpose * A
  let val1, vec1 = eig L // each row of vec1 is an eigenvector
  // get the eigen values and eigen vectors for Cov(A)
  let v = val1 * (1.0 / float (ncol - 1))
  let u = A * vec1.Transpose

  // normalize eigen vectors
  let mutable cnt = 0
  for i=0 to ncol-1 do
      if abs v.[i] < 1e-8 then
          u.[0..nrow-1,i..i] <- Matrix.create nrow 1 0.0
      else
          cnt <- cnt + 1
          let norm = Vector.norm (u.[0..nrow-1,i..i].ToVector())
          u.[0..nrow-1,i..i] <- u.[0..nrow-1,i..i] * ( 1.0 / float norm )

  // sort
  // let u' = u.PermuteColumns (fun j -> j ) //u.NumCols - j - 1)
  // the PermuteColumns function is buggy
  let u' = Matrix.init u.NumRows u.NumCols (fun i j -> u.[i, u.NumCols - j - 1])

  let v' = v.Permute (fun j -> v.NumRows - j - 1)

  let select = min cnt numVecs
  //printfn "%A" select
  if cnt < numVecs then
      printfn "warning: numvec is %d; only %d exist." numVecs cnt

  let v1 = v'.[0..(select-1)]
  let u1 = u'.Columns(0, select)
  let transformed = (u1.Transpose) * A
  v1, u1, colm, transformed

and:

let eigenface (p:matrix array) numVecs =
  let B = p |> Array.map mat2vec
  let nrow = B.[0].Length // nrow is big  == # of elements in a face
  let ncol = B.Length  // # of faces for a person
  // put a 2d face into a vector as a column in matrix A
  let A = Matrix.init nrow ncol (fun i j -> B.[j].[i])

  let v, u, mface, transformed = eigCov A numVecs
  (*
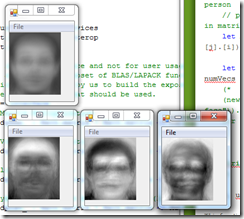
  (new PGMViewer(vec2mat mface 112 92, "mean face")).Show()
  for i=0 to 2 do
      let eface = scale (u.Column(i))
      let f = vec2mat eface 112 92
      (new PGMViewer(f, "eigenface " + i.ToString())).Show()
  *)

  v, u, mface, transformed

This function transform an image matrix into a vector and call the eigCov to get the eigenfaces. The commented lines in this function is used to output the mean face and the first 3 eigenfaces:

Use eigenfaces to do recognition for a new face:

let recognition (u:matrix) (mface:vector) (transformed:matrix) (face:vector) =

    let d = face - mface
  let t = u.Transpose * d

  let distance a b = Vector.norm (a - b)
  {0..transformed.NumCols-1}
  |> Seq.map (fun j -> distance t (transformed.Column(j)), j)
  |> Seq.min
  |> snd

To put the recognition into a learning and testing framework:

let learning data =
  let train, test = splitDataSet data
  let dat, lab = strip train
  let dat0, lab0 = strip test
  let v, d, mface, tran = eigenface dat 10

  let correctCnt =
      dat0
      |> Seq.mapi (fun i f ->
              let idx = recognition d mface tran (mat2vec f)
              let label = lab.[idx]
              if label = lab0.[i] then 1 else 0
          )
      |> Seq.sum
  float correctCnt / (float dat0.Length)

Using 10 most significant eigen faces from the 280(7 * 40) faces, we recognize the remaining 120(3 * 40) faces, and get 113 faces recognized to the correct person, thus a 94.17% accuracy, which is reasonable good considering that we have done any normalization on the faces, and the classifier is only 1 nearest neighbor.

Remark

In this post, we have seen that how F# could be used as an prototype tool like Matlab. In the matrix computation part, we need to write some utility functions ourselves, while in Matlab they are built in. However, the strength of F# comes from the language part, we could control the training and testing more freely than in Matlab. Moreover, once we have developed this face recognition component, it is just straightforward to use C# or VB.Net to call it.

Although we have a high accuracy in the final test, the result is only for a well prepared dataset. In real situations, things would be very hard. Maybe over 90% time is spent on tuning best parameters and preprocessing the face images.