北航研究生《算法设计与分析》期末复习整理

课程名称：算法设计与分析

参考往年题来源：TheBloodthirster/BUAA_Course_Sharing

数据结构

二叉树

线索二叉树(Threaded Binary Tree）

利用二叉链表中空的指针域指出结点在某种遍历序列中的直接前驱或直接后继

指向前驱和后继的指针称为线索

实现不用栈的树深度优先遍历算法

二叉查找树(Binary Search Tree, BST）

左子树都更小，右子树都更大

建立：逐点插入法

平衡二叉树(Adelson-Velskii and Landis, AVL）

左子树和右子树的深度之差的绝对值不超过1

最坏情况下插入和查找的时间复杂度为O(log2n)

堆(Heap)

一种特殊类型的二叉树

（1）每个节点的值大于（或小于）等于其每个子节点的值

（2）该树完全平衡，其最后一层的叶子都处于最左侧的位置。

大顶堆的根节点包含了最大的元素，小顶堆的根节点包含了最小的元素

哈夫曼树(Huffman Tree）

给定一组权值，构造出的具有最小带权路径长度(WPL, weighted path length)的二叉树

优先队列(Priority queue）

权值越大的叶结点离根结点越近，权值越小的叶结点离根结点越远

多叉树

B树(Balanced Tree)

m阶B树是平衡的m路搜索树

根结点至少有两个孩子；
每个非根节点所包含的孩子个数 $j$ 满足： $\lceil m/2 \rceil \leq j \leq m$
每个叶节点的关键字个数 $k$ 满足： $\lceil m/2 \rceil- 1 \leq k \leq m - 1$
具有 n 棵子树的结点中一定有n 个关键字
key[i] 和 key[i+1] 之间的孩子节点的值介于 key[i] 和 key[i+1] 之间
所有的叶子结点都位于同一层

2-3树

最简单的B树结构
每个非叶节点都有两个或三个子女，而且所有叶都在统一层上

B+树

B树基础上

叶结点中存放记录的关键字以及指向记录的指针

叶结点按关键字值的大小顺序链接成线性链表

所有分支结点可以看成是索引的索引

结点中仅包含它的各个孩子结点中最大(或最小)关键字值和指向孩子结点的指针

图

存储
- 邻接矩阵存储：顶点 i 到 j 用A[i][j]表示是否有边、权重
- 邻接表存储：每个顶点一个线性链表，存它作为起始点的所有边和权重
  
  逆邻接表存储：每个顶点一个线性链表，存它作为目标点存所有边和权重
遍历
- 深度优先遍历(Depth First Search,DFS)
- 广度优先遍历(Breadth First Search,BFS)

最小生成树

生成树：包含具有n个顶点的连通图G的全部n个顶点, 仅包含其n-1条边的极小连通子图称为G的一个生成树
最小生成树：带权连通图中，总的权值之和最小的带权生成树
普里姆Prim算法：O(V^2)
- 依次在G中选择一条一个顶点仅在V中、另一个顶点在U中,并且权值最小的边加入集合TE，同时将该边仅在V中的那个顶点加入集合U
- 算法的每一步都是一棵生成树
克鲁斯卡尔Kruskal方法：O(E log V)
- 符合拟阵的遗传和交换性质
- 从G中选择一条当前未选择过的、且边上的权值最小的边加入TE，若加入TE后使得T未产生回路,则本次选择有效
破圈法(管梅谷)

从赋权图G的任意回路开始，去掉该圈中权值最大的一条边，称为破圈。不断破圈，直到G中没有回路为止

最短路径问题

Dijkstra算法：贪心单源最短路径算法 O(E + V*log(V))
在那些尚未找到最短路径的顶点中确定一个与源点v最近的顶点u
- 将源点v到顶点u的(最短)路径长度分别加到源点v通过顶点u可以直接到达、且尚未找到最短路径那些的顶点的路径长度上
局限性：负权重回路
弗洛伊德 Floyd-Warshall 算法：动态规划多源最短路径算法 O(V^3)
1. 初始时，对于任意两个顶点，若他们之间存在边，则以此边上的权值作为它们之间的最短路径长度，若不存在有向边，则以∞作为它们之间的最短路径长度，
2. 之后逐步尝试在原路径中加入顶点作为中间顶点，如果增加中间顶点后，得到的路径比原来的路径短，则以此新路径代替原路径。

欧拉图

欧拉通路：对于图G来说，如果存在一条通路包含G中所有的边，则该通路成为欧拉通路，也称欧拉路径。
欧拉回路：如果欧拉路径是一条回路，那么称其为欧拉回路。
欧拉图：含有欧拉回路的图是欧拉图。
奇点：图中跟这个点相连的边的数目为奇数个的点
定理1：存在欧拉路的条件：无向图是连通的，有且只有2个奇点。
定理2：存在欧拉回路的条件：无向图是连通的，有0个奇点。
定理3：对于有向图而言，存在欧拉回路的条件是，所有点的出度和入度相等；或者有且仅有两个点的出度和入度不相等，则该两点一个为起点（出度比入度多1），一个为终点（入度比出度多1），则存在欧拉路。
求欧拉路的算法
（1）求各个点的度，并判断是否是欧拉回路
（2）从奇点（或者任意点）开始DFS，并记录路径
（3）避免重复走边，遍历过的边删除
（4）时间复杂度：O(V+E)

哈密顿图

NP难问题
哈密尔顿路径HP：通过图G中每个顶点一次且仅一次的道路称作该图的一条哈密尔顿道路.
哈密尔顿回路HC：通过图G中每个顶点一次且仅一次的道路称作该图的一条哈密尔顿回路.
哈密尔顿图：存在哈密尔顿回路的图称作哈密尔顿图
哈密顿回路移走任何一条边都会产生一棵生成树T

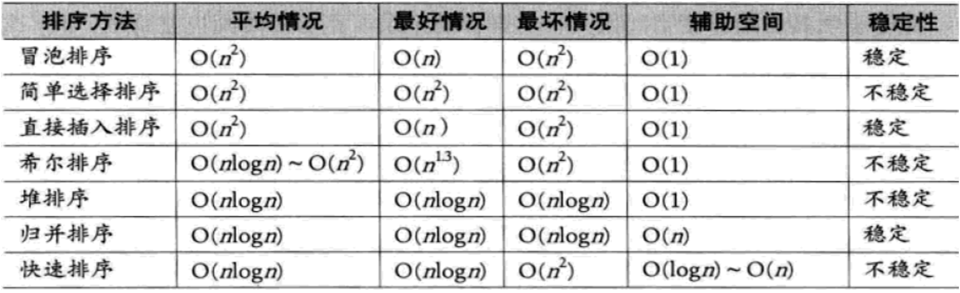
排序

稳定排序：对于值相同的两个元素，排序前后的先后次序不变，则称该方法为稳定性排序方法
插入排序：
选择排序：
冒泡排序：
shell希尔排序：
堆排序：
二路归并排序：
快速排序：

随机快速排序：pivot的选择随机，不会固定被升序/降序/全相同输入触发n^2最坏情况
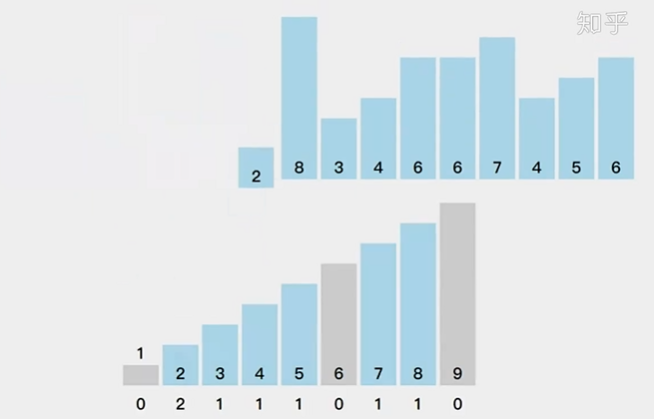
计数排序：牺牲内存空间来换取低时间复杂度的排序算法，不基于比较的算法。

算法

常见题型

五大常用算法：分治、动态规划、贪心、回溯、分支界定

双指针(面试)

防止溢出：
- 双指针和查找 nums[i] + nums[j] == target => target - nums[i] == nums[j]
- 二分查找 (left + right) / 2 => left + ((rigth - left) >> 1))

重合的起始位置：

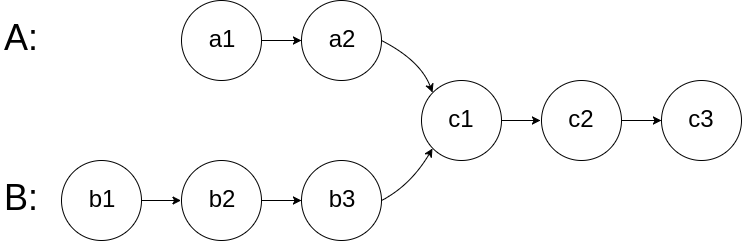
我的做法：先遍历知道长度nA和nB后，长的先跑|nA-nB|

int n = max(nA, nB);
ListNode *pA = lA, *pB = lB;
while (n > 0) {
    if (pA == pB) return pA;
    if (n <= nA) pA = pA->next;
    if (n <= nB) pB = pB->next;
    n--;
}

优雅做法：p1遍历lA+lB，p2遍历lB+lA，第一次相同就是重合的指针或者NULL

ListNode *p1 = lA, *p2 = lB;
while (p1 != pB) {
    p1 = (p1 == NULL) ? lB : p1->next;
    p2 = (p2 == NULL) ? lA : p2->next;
}

环的起始位置：

随机算法

Las Vegas 拉斯维加斯算法：采样越多，越有机会找到最优解
Monte Carlo 蒙特卡罗算法：采样越多，越近似最优解

在Monte Carlo算法后加上一个验证算法，如果正确就得到解，如果错误就不能生成问题的解，就会转化成Las Vegas算法。

通过多次运行Monte Carlo，并且满足每次运行时的随机选择都相互独立，使产生非正确解的概率可以减到任意小，转化为Las Vegas算法

减治分治变治

分治：

将一个规模为N的问题分解为K个规模较小的子问题，最常见二分法O(logn)

示例：连续子数组的最大和
连续天数的最高销售额
推荐阅读线段树区间合并法解决多次询问的「区间最长连续上升序列问题」和「区间最大子段和问题」
减治：

一个大问题划分为若干个小的子问题，但是这些子问题不需要分别求解，只需要求解其中一个子问题便可

３种主要的变种：
- 减去一个常量 (decrease by a constant)：
  例如深度优先，广度优先查找，拓扑排序，插入排序，生成排序
- 减去一个常数因子(decrease by a constant factor)：
  二分搜索，假币问题，折半查找
  俄式乘法：n是偶数n * m = n / 2 * 2m ，n是奇数n * m = (n-1) / 2 * 2m + m
  约瑟夫问题(报数被杀)：n是偶数J(2k)=2J(k)-1，n是奇数J(2k+1)=2J(k)+1
- 减去的规模是可变的(variable size decrease)：
  二叉查找树最差O(n) 平均O(logn)，插值查找最差O(n)
  欧几里得算法求最大公约数 $gcd(a,b)=gcd(b,a~mod~b)$
变治：

把问题的实例变得容易求解，然后进行求解
- 实例化简(Instance simplification)：将原问题变换为同样问题的一个更简单或者更方便的实例
  例如预排序，AVL树(带了平衡功能的二叉查找树)(?)
- 改变表现(Representation Change)问题化简(Problem reduction)：将原问题变换为同样实例的不同表现
  例如霍纳法则计算多项式 $p(x)=(\dots(a_bx+a_{n-1})x + \dots)x+a_0$
  平衡查找树(?)
  2-3 树(?)
  堆和堆排序
- 问题化简(Problem reduction)：将原问题变换为另一个已知问题的实例
  例如将背包问题转化为n维线性规划
  最小公倍数：通过两数乘积与其最大公约数之商求得
  函数极值：已知最小求最大，目标函数加负号

回溯法

按深度优先策略搜索问题的解空间树

贪心算法

贪心算法每一步必须满足：可行的、局部最优、不可撤销

思路：

①建立数学模型来描述问题

②把求解的问题分成若干个子问题

③对每个子问题求解，得到子问题的局部最优解

④把子问题的解局部最优解合成原来解问题的一个解
问题：
- 不能保证是全局最优解
- 不能用来求最大值或最小值的问题
- 只能求满足某些约束条件的可行解的范围
典型案例：
求最小生成树的Prim算法和Kruskal算法
- 最短路径Dijstra算法
- 哈夫曼编码
拟阵：拟阵是一个满足如下条件的有序对：M=(S,I)
- S 是非空有限集
- I 是 S 子集的一个非空族，这些子集称为 S 的独立子集，I 满足遗传性质，若B∈I, 且A⊆B, 则 A∈I
  若 B 是 S 的独立子集，则 B 的任意子集均是 S 的独立子集
- I 满足交换性质，若A∈I , B∈I 且 ∣A∣<∣B∣ 则存在某个元素 x∈ B-A 使得 A∪{x}∈I

动态规划

概念：
- 阶段：求解第n个子问题称为第n个阶段。动态规划是按照顺序去求解子问题的，这里子问题的求解顺序很重要
- 状态：在求解第n个阶段时，已求解n-1个阶段的解，称为状态
- 决策（状态转移）：在求解第n个阶段时，根据状态和计算规则，可以得到第n个阶段时解。

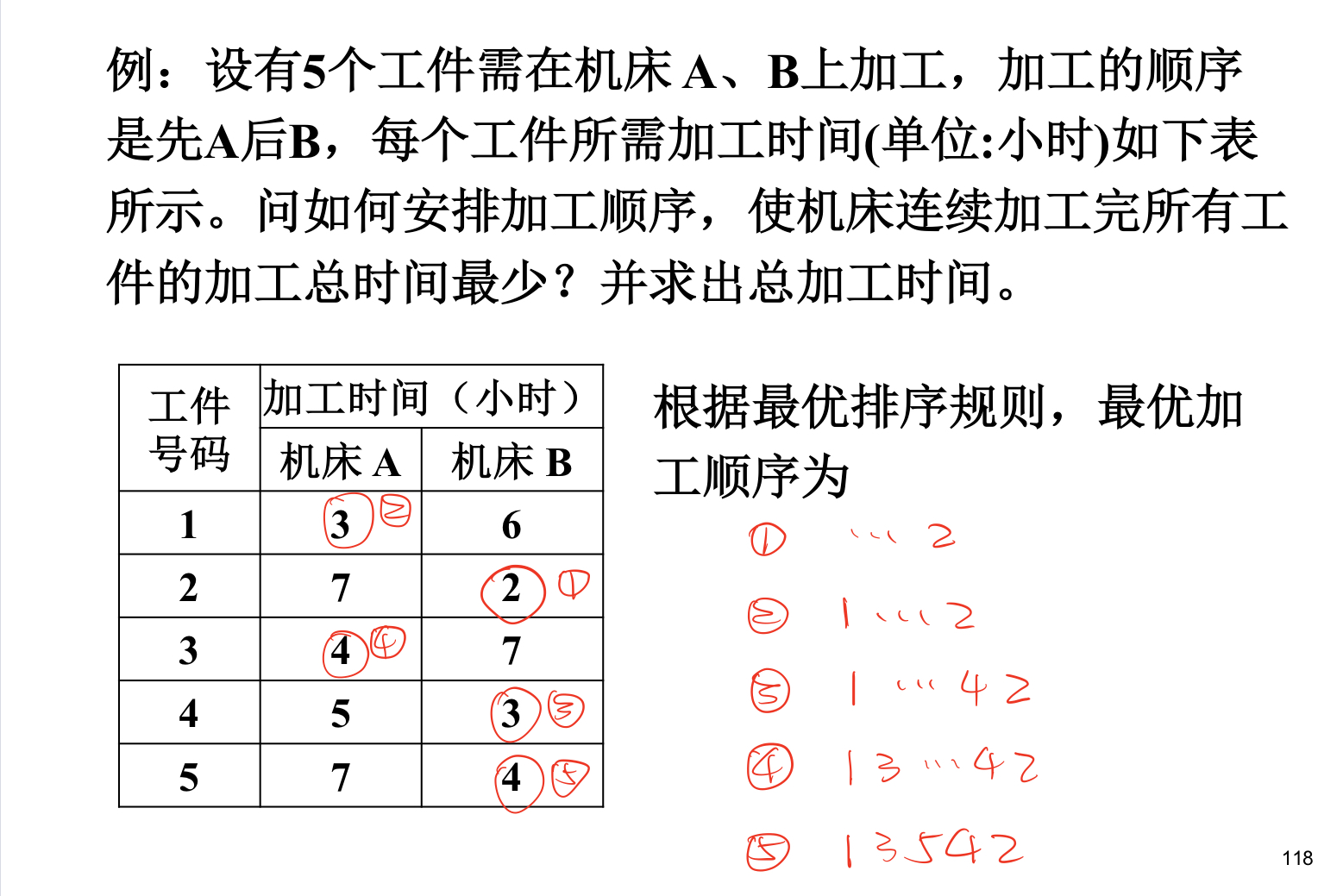
最优排序规则

有n个工件需要在机床A、B 上加工，每个工件都必须经过先A而后B的两道加工工序，时间分别为ai和bi

f(X, t, i, j)：在A上相继加工 i 与 j 后，对以后的加工工件X采取最优顺序，全部加工完需要的时间t

$f(X, t, i ) = a_i + f(X –\{i\}, z_i (t))$ ，其中 $z_i (t) = max ( t – a_i , 0)+ b_i$

$f(X, t, i, j) = a_i + a_j + f(X –\{i,j\}, z_{ij} (t))$

$z_{ij}(t) = max[ t – a_i – a_j + b_i + b_j , b_i +b_j – a_j , b_j ] \\ z_{ji}(t) = max[ t – a_i – a_j + b_i + b_j , b_i + b_j – a_i , b_i ]$

$z_{ij}(t) \leq z_{ji}(t)$ 等价于 $min(a_i , b_j) ≤ min(a_j , b_i )$

例题：

最长公共子序列

L[i, j] 表示 A=a1a2…ai 和 B=b1b2…bj的最长公共子序列的长度

递推关系：

L [i, j] = {\begin{cases} \begin{aligned} (1) & 0, & 若 i = 0 或 j = 0 \\ (2) & L [i - 1, j - 1] + 1, & 若 i > 0, j > 0, a_{i} = b_{j} \\ (3) & m a x (L [i, j - 1], L [i - 1, j]), & 若 i > 0, j > 0, a_{i} \neq b_{j} \end{aligned} \end{cases}

$L[i,j] = \begin{cases} \begin{align} &0,& &若i=0或j=0 \\ &L[i-1, j-1] + 1,& &若i > 0,~j > 0,~a_i = b_j \\ &max(L[i, j-1], L[i-1, j]),& &若i > 0,~j > 0,~a_i \neq b_j \\ \end{align} \end{cases}$

矩阵链相乘

执行矩阵乘法M1M2…Mn 所需的数量乘法的最小次数C[1,n]

乘法： $(M_i \dots M_{k-1})~(M_k \dots M_j)$

其中， $r_i$ 与 $r_{i+1}$ 分别是 $M_i$ 的行数和列数

递推关系： $C[i,j]=\displaystyle \min_{i<k\leq j}(C[i,k-1]+C[k,j]+r_ir_kr_{j+1}),~1\leq i<j\leq n$

最短路径问题

Floyd-Warshall算法

D[i, j]=min{D[i, j], D[i, k] +D[k, j]}

算法的运行时间是 $Θ(n^3)$

有向图的传递闭包

从第 i 个顶点到第 j 个顶点之间存在一条有向路径则 $t_{ij}=1$

Warshall 算法

定义矩阵 $R^{(k)} = (r_{ij}^{(k)})_{n \times n}$

从顶点 i 到顶点 j 存在一条长度大于0 的有向路径且路径的每一个中间顶点的编号不大于k时 $r_{ij}^{(k)}=1$

初始状态 $R^{(0)}$ 为邻接矩阵，问题所求为 $R^{(n)}$

递推关系： $r_{ij}^{(k)}=r_{ij}^{(k-1)} \vee (r_{ik}^{(k-1)} \wedge r_{kj}^{(k-1)})$

最优二叉查找树问题

设 $T_i^j$ 是由键 $a_i , \dots, a_j$ 构成的二叉树，键的查找概率分别为 $p_1, \dots, p_n$ ，C[i, j]是在这棵树中成功查找的最小的平均查找次数

所求最优二叉查找树和平均次数为 $T_1^n$ 和 C[1, n]

递推关系： $C[i, j]=min_{i \leq k \leq j}(C[i, k-1] + C[k+1, j]) + \sum_{s=i}^jp_s$

01背包问题

n 项物品的集合U={u1, u2,…, un}，其中物品 uj 的体积为 sj 价值为 vj(1≤ j≤ n) ，背包容量 C

V[i, j]: 从前 i 项物品中取出来的装入体积为 j 的背包的最大价值总和

递推关系：

L [i, j] = {\begin{cases} \begin{aligned} (4) & 0, & 若 i = 0 或 j = 0 \\ (5) & V [i - 1, j], & 若 j < s_{i} \\ (6) & m a x (V [i - 1, j], V [i - 1, j - s_{i}] + v_{i}), & 若 j \geq s_{i} \end{aligned} \end{cases}

$L[i,j] = \begin{cases} \begin{align} &0,& &若i=0或j=0 \\ &V[i-1, j],& &若j<s_i \\ &max(V[i-1, j], V[i-1, j-s_i]+v_i),& &若j\geq s_i \\ \end{align} \end{cases}$

矩阵快速幂

如需求数据 a 的幂次，此处 a 可以为数也可以为矩阵，常规做法需要对a进行不断的乘积即 a * a * a * ... 此处的时间复杂度将为 O(n)

3^10=3*3*3*3*3*3*3*3*3*3
    =9^5 =9^4*9 =81^2*9 =6561*9

基于以上原理，我们在计算一个数的多次幂时，可以先判断其幂次的奇偶性，然后：

如果幂次为偶直接 base(底数) 作平方，power(幂次) 除以2
如果幂次为奇则底数平方，幂次整除于2然后再多s乘一次底数

对于以上涉及到 [判断奇偶性] 和 [除以2] 这样的操作。使用系统的位运算比普通运算的效率是高的，因此可以进一步优化：

把 power % 2 == 1 变为 (power & 1) == 1
把 power = power / 2 变为 power = power >> 1

斐波那契数列：

[\begin{matrix} F (n + 1) \\ F (n) \end{matrix}] = [\begin{matrix} F (n) + F (n - 1) \\ F (n) \end{matrix}] = [\begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix}] [\begin{matrix} F (n) \\ F (n - 1) \end{matrix}] = {[\begin{matrix} 1 & 1 \\ 1 & 0 \end{matrix}]}^{n} [\begin{matrix} F (1) \\ F (0) \end{matrix}]

$\begin{bmatrix} F(n+1) \\ F(n) \end{bmatrix} = \begin{bmatrix} F(n) + F(n-1) \\ F(n) \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} F(n) \\ F(n-1) \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}^n \begin{bmatrix} F(1) \\ F(0) \end{bmatrix}$

根据递推关系，我们可以得到：对于如下矩阵运算，有 c = a^n * b，其中：

a = [[1,1], [1,0]], 
b = [F(1), F(0)],
c = [F(n+1), F(n)]

题解：时间复杂度 $O(\log{n})$ ，空间复杂度 $O(1)$

class Solution {
public:
    const int MOD = 1000000007;

    int fib(int n) {
        if (n < 2) {
            return n;
        }
        vector<vector<long>> q{{1, 1}, {1, 0}};
        vector<vector<long>> res = pow(q, n - 1);
        return res[0][0];
    }

    vector<vector<long>> pow(vector<vector<long>>& a, int n) {
        vector<vector<long>> ret{{1, 0}, {0, 1}};
        while (n > 0) {
            if (n & 1) {
                ret = multiply(ret, a);
            }
            n >>= 1;
            a = multiply(a, a);
        }
        return ret;
    }

    vector<vector<long>> multiply(vector<vector<long>>& a, vector<vector<long>>& b) {
        vector<vector<long>> c{{0, 0}, {0, 0}};
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                c[i][j] = (a[i][0] * b[0][j] + a[i][1] * b[1][j]) % MOD;
            }
        }
        return c;
    }
};

分支定界算法

对问题的解空间树进行搜索：

产生当前扩展结点的所有孩子结点。
在产生的孩子结点中，抛弃那些不可能产生可行解(或)最优解的结点（剪枝）。
将其余的孩子结点加入活结点表。
从活结点表中选择下一个活结点作为新的扩展结点。

如此循环，直到找到问题的可行解(最优解)或活结点表为空。

分类：

FIFO(First In First Out) 分支定界算法：按照先进先出原则选择下一个活结点作为扩展结点，即从活结点表中取出结点的顺序与加入结点的顺序相同。
最小耗费或最大收益分支定界算法：在这种情况下，每个结点都有一个耗费或收益。假如要查找一个具有最小耗费的解，那么要选择的下一个扩展结点就是活结点表中具有最小耗费的活结点，假如要查找一个具有最大收益的解，那么要选择的下一个扩展结点就是活结点表中具有最大收益的活结点。

时间复杂度

上下界符号

$\Theta$ ，既是上界也是下界(tight)，就是相等，准确的复杂度

$Ο$ ，表示渐进上界(tightness unknown)，小于等于的意思，近似复杂度。

$ο$ ，表示上界(not tight)，小于的意思，明确的知道小于它，准确计算出来的。

$\Omega$ ，表示渐进下界(tightness unknown)，大于等于的意思，近似复杂度。

$\omega$ ，表示下界(not tight)，大于的意思，明确的知道大于它，准确计算出来的。

寻找下界的策略：

平凡下界：对问题的输入中必须要处理的项及必须要输出的项进行计数
信息量论证
对手规约
问题规约

NP问题

P问题：多项式时间内可以解决的问题

NP问题：非确定性图灵机在多项式时间内可以解决的问题

NP完全问题：能够完全模拟复杂性类（即所有NP）的问题；所有的NP问题都可以约化到NP完全问题

NP难问题：1）NP完全问题。2）比NP完全问题还难的问题

伪多项式算法：在输入实例中的最大数值的多项式时间内运行，属于NPC问题

判定问题：

优化问题：

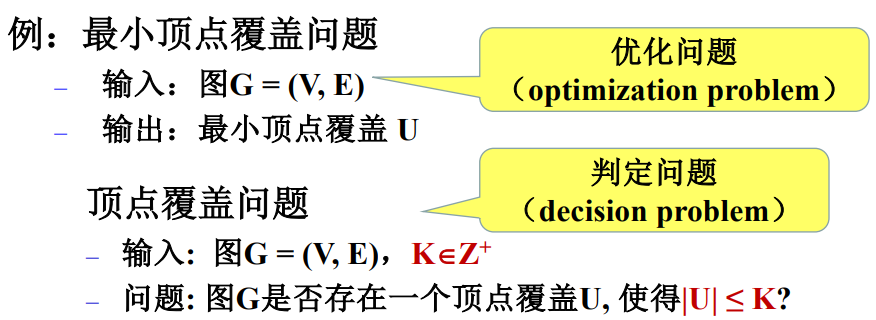
多项式时间归约：判定问题P1多项式时间内可以归约成问题P2，则P2至少和P1一样难

近似算法

定义

r-近似：近似算法最坏情况小于等于所求全局最优结果的r倍（精度<=r）

ε-近似：相对误差 <= ε
多项式近似方案(PAS, Polynomial-time Approximation Scheme)：
- 每一个算法AƐ 在输入实例 I 的规模的多项式时间内运行
- 采用附加参数 ε > 0，并提供近似于 (1 + ε) 的最小化解和 (1 – ε) 的最大化解
- 运行时间必须是 n 的多项式，但是可以是 ε 的指数
完全多项式近似方案(FPAS, Fully Polynomial-time Approximation Scheme)：
- 每个算法 AƐ 在以输入实例的规模和1/Ɛ两者的多项式时间内运行
- 算法需要对问题大小 n 和 1/ε 进行多项式计算
- 近似算法的复杂度和精度要求有关
伪多项式算法：在输入实例中的最大数值（而不是输入的规模）的多项式时间内运行
- 定义：时间复杂度可以表示为输入数值N的多项式，但其运行时间与输入数值N的二进制位数呈指数增长关系
- 为NP难问题找到一个FPAS的想法对存在伪多项式时间算法的问题来说是很典型的。可以对实例 I 的输入值应用尺度变换和舍入得到实例 I' 并解之
- 对于子集和问题，算法的近似度是 1+ε ，运行时间是 (n^2/ε)

贪心算法

最小顶点覆盖

贪心算法不是r-近似算法
- 贪心思想解决最小顶点覆盖问题：重复选择度数最高的顶点，并去掉所有邻接边
- 反例：（参考StackExchange）
  
  考虑一个可分为左右两个互不相交的顶点子集 $V_L$ 和 $V_R$ 的二分图
  
  左顶点集 $V_L$ 中包括 $n$ 个顶点，右顶点集 $V_R$ 由 $n-1$ 个顶点集合 $V_{R,2}, V_{R,3}, \cdots, V_{R,n}$ 组成
  
  其中 $V_{R,i}$ 顶点集中的每个顶点分别与左侧的 $i$ 个顶点连接，即有该顶点集包含 $\lfloor \displaystyle \frac{n}{i} \rfloor$ 个度数为 $i$ 的顶点
  
  由调和级数公式可知，右顶点集顶点总数为 $\displaystyle\sum_{i=2}^ n{\frac{n}{i}} = \Omega(n~\log{n})$
  
  对于贪心算法，初始状态左顶点集 $V_L$ 每个顶点度数为 $n-1$ ，优先选择度数为 $n$ 的右侧顶点集子集 $V_{R,n}$ ，去掉对应的边后左顶点集每个顶点度数为 $n-2$ ，仍然选择右侧顶点集子集
  
  即有贪心算法选择右侧 $V_R$ 所有顶点，而最小覆盖问题的最优解是选择左侧 $V_L$ 所有顶点
  
  对于此情况，贪心算法的近似系数为 $\displaystyle \frac{num(V_R)}{num(V_L)} = \Omega(\frac{n~\log{n}}{n})=\Omega(\log{n})$
  
  当顶点数 $n$ 无穷大时，近似系数 $log~n$ 无穷大，所以贪心算法不是r-近似算法
2-近似算法：（参考GeeksForGeeks和肯特州立大学学生博客）
- 从边集合E中选取任意边(u, v) 并将“u”和“v”添加到结果中删除E中与u或v相关的所有边
- 证明2-近似：
  
  设最优解得到顶点覆盖的顶点集合为 $S_{opt}$ ，近似解的顶点集合为 $S$ ，所有被选取的边的集合为 $A$
  
  由于选取边(u, v)后删除以u或者v为顶点的所有边，A中没有两条边被 $c_{opt}$ 的同一顶点覆盖，即有下限 $|S_{opt}|\geq |A|$
  
  每加入A中的一条边向结果加入两个顶点，即有 $|S| = 2|A|$
  
  因此有 $|S|\leq 2|S_{opt}|$ ，得证为2-近似算法
变式：带权顶点覆盖问题
- 定价策略(pricing method)：（参考Github源码和普林斯顿大学讲义pdf）
  
  图G(V,E)，每次选择u和v的剩余权重都高于 $p_e$ 的边(i, j)，将其中较小的顶点加入结果顶点集合 $S$ ，设置较小顶点的权重为边的价格 $p$ 并将边加入集合 $A$ ，两个顶点的权重都减去其中
  
  $w(S) = \displaystyle\sum_{i\in S}w_i = \sum_{i\in S} \sum_{e=(i,j)}p_e \leq \sum_{i\in V} \sum_{e=(i,j)}p_e = 2 \sum_{e\in E}p_e \leq 2w(S_{opt})$

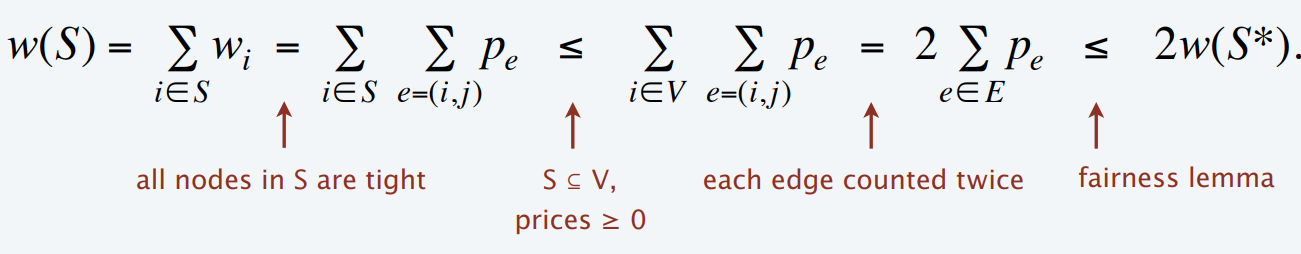
最小集合覆盖

不存在 r-近似算法
维基百科：下界为 $(1-o(1))~ln~n$ （除非 $P=NP$ ）
集合覆盖问题的贪心算法不是r-近似算法
- 贪心算法：依次选择未加入当前顶点集的顶点最多的集合
- 反例：（参考维基百科和StackOverflow）
  如下的5个集合，贪心算法依次选择从右到左的三个两行的集合，而最优解是上下两个各一行的集合，近似系数3/2
  
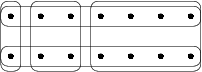
  上述反例可以拓展到有n个两行的矩形，近似系数n/2
变式：加权集合覆盖问题（参考GeeksForGeeks和麻省理工讲义pdf）
- 贪心算法：每一轮计算剩下的所有集合 $S_i$ 的权重成本 $\displaystyle \frac{w_i}{|S_i-C|}$ ，将最小成本的对应集合加入当前集合覆盖并更新对应顶点集合C，直到C为全集U
  - 证明不是r-近似算法的例子同上面的反例
  - 证明是 $log~n$ 近似：
    设 OPT 为最优解对应最小权重和，假设在上述贪心算法迭代之前覆盖了(k-1)个元素，则第 k 个元素的权重 $w_k \leq\displaystyle\frac{OPT}{n-k+1}$
    
    则有近似算法的权重和 $\displaystyle \sum_{k=1}^n w_k ≤ ∑_{k=1}^n \frac{OPT}{n-k+1} = OPT∑_{k=1}^n \frac{1}{k}=OPT*logn$
- 威斯康星大学讲义pdf写了好几种近似算法但是都是logn级别的

最小工期分配

最小工期分配问题的列表调度贪心算法是2-近似算法：

给定 $m$ 台机器 $M_1, \cdots, M_m$ 和 $n$ 项作业，每一项作业 $j$ 的处理时间为 $t$ 。设 $A_i$ 为分配给机器 $M$ 的作业集合，机器 $M$ 需要工作的时间为 $T_i=\sum_{j\in S(i)}t_j$ ，称 $T_i$ 为机器 $M$ 的负载。求出调度方案 $A(1),A(2),\cdots,A(m)$ 使得工期，即所有机器的最大负载 $T=\max{T_i}$ 最小。
等效问题：二划分问题
对于正整数集合 $A=\{a_1,a_2,\cdots,a_n\}$ 和正整数 $T_{opt}=\frac{1}{2} \sum_{j=1}^n a_j$ ，能否找到集合 $A$ 的二划分 $\{A_1,~A_2\}$ 使得 $\sum_{a_j\in A_1}a_j = \sum_{a_j\in A_2}a_j = T_{opt}$
当机器数 $m=2$ 时，将最小工期分配调度问题转化为上述二划分问题，所求为两个机器负载相同的情况
列表调度(List scheduling)：
重复执行以下步骤，直到获得有效的调度：
①执行作业列表中的第一个作业
②找到当前负载最小的机器，将该作业安排在该机器上
证明列表调度为2-近似算法：
- 方法一：（参考StackExchange和多伦多讲义pdf）
  假设最大负载 $T$ 对应的机器为 $M_i$ ，该机器上安排的最后一个作业为 $j$ ，由列表调度贪心算法规则可知在安排作业 $j$ 之前机器 $M_i$ 是负载最小的机器，小于当时的平均负载，即有：
  
  $\begin{align*} T &= (T - t_j) + t_j \\ &\leq \frac{(\displaystyle\sum_{1 \leq k \leq m}{T_k}) - t_j}{m} + t_j \\ &= \frac{1}{m} \displaystyle\sum_{1 \leq k \leq m}{T_k} + (1-\frac{1}{m})t_j \\ &\leq T_{opt} + (1-\frac{1}{m})T_{opt} \\ &= (2-\frac{1}{m})T_{opt} \end{align*}$
  即有该列表调度贪心算法近似系数为 $\displaystyle 2-\frac{1}{m}$
- 方法二：（参考弗莱堡大学算法讲义pdf）
  设最优解对应最小工期为 $T_{opt}$ ，若能证明该贪心算法所有作业 $j$ 开始工作时间 $s_j \leq T_{opt}~(j=1 \dots n)$ ，则有作业 $j$ 结束时间 $c_j = s_j + t_j \leq T_{opt}+t_j \leq 2*T_{opt}$ ，即为2-近似算法
  反证法：如果存在作业 $j$ 开始工作时间 $s_j > T_{opt}$ ，则该作业开始时所有机器的负载都大于 $T_{opt}$ ，即有 $\sum_{j'\in J'} t_{j'} > m*T_{opt}$ (其中 $J'$ 是 $J$ 的子集，对应着作业 $j$ 之前完成的所有作业)，与最小工期 $T_{opt}$ 对应着所有任务完成总时间 $\sum_{j \in J} t_j \leq m*T_{opt}$ 矛盾

旅行商问题TSP

Travelling Salesman Problem，TSP

给定一系列城市和每對城市之间的距离，求解访问每座城市一次并回到起始城市的最短回路（哈密顿回路）

贪心：最近邻（nearest-neighbor）算法
- 下一次总是访问最近的未访问城市
- 对于实例 $I$ 和最近邻算法的解回路 $s_a$ ，只要权重w任意大，结果 $R(I’ , sa)$ 可以任意大
- 近似因子 $\Theta(log~|V|)$
证明不存在 r-近似算法

证明TSP问题有多项式时间r-近似算法等价于哈密顿回路HC问题有多项式时间解法（与HC问题是NPC问题矛盾）

任何一个HC问题实例 $G$ 都可以通过下面的方式背多项式时间内规约为TSP问题r-近似 $G'$ ：
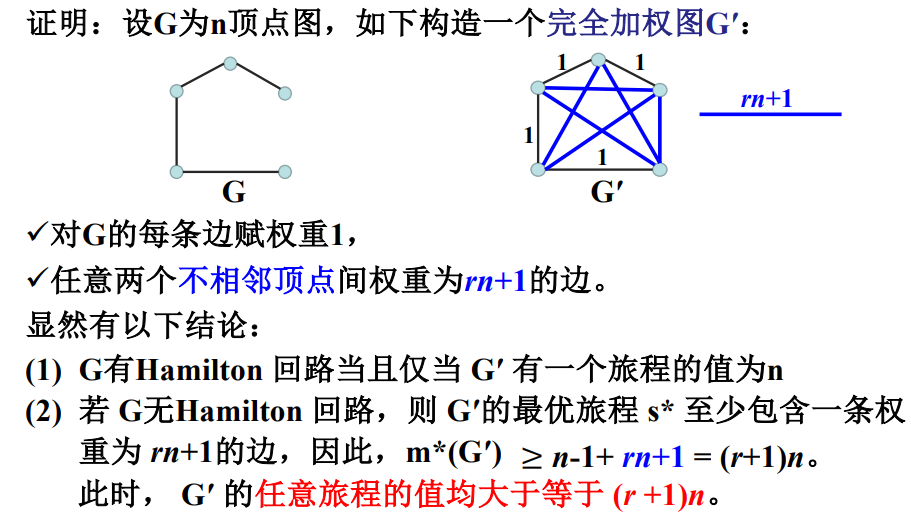
简化变式：欧几里得类型旅行商问题（Euclidean TSP）
- 城市间的距离满足三角不等式和对称性
- 最近邻居算法近似系数： $\frac{1}{2} (\lceil log_2n \rceil + 1)$ (?)
- 绕树两周算法：2-近似算法
  
  最终路径长度<=2*最小生成树两周长度<=2*哈密顿路径程度（哈密顿路径移除一条边是一棵生成树）
- Christofide算法：1.5-近似算法
  
  找出最小生成树 T*，找出T*中度数为奇数的顶点集合X，在X中寻找d最小权重匹配 M，在多重图 T* ∪ M 中寻找欧拉回路 $t_e$ ，删除 $t_e$ 中已访问过的顶点得到解 t
  
  $m(x, t) ≤ f(t_e) ≤ f(T^*) + f(M) < m^*(x) + m^*(x)/2 =1.5~m^*(x)$

背包问题

01背包问题
- n个物品集合U，重量 $w_i$ ，价值 $v_i$ ，背包承重W，求价值最高的物品子集
- 等价整数划分问题、线性规划问题
- 贪心算法：把物品按价值重量比vi /wi 降序排序，按列表序放能放入的物品
  
  特例：重1价2+重W价W，解的性能比为 W/2 没有上界 ∞
- 增强贪心算法：
  
  max（贪心算法的解，能放入箱子的物品中具有最大价值的物品）
  
  证明2-近似算法：考虑第一个不能放入箱子中的物品
- S.Sahni 算法：性能比1+1/k，0 ≤k<|x|(?)
  
  生成所有小于等于 k 个物品的子集，对每个可行子集S'按贪心原则对 S'增加剩余物品成为S''，输出最大S''

线性规划

0-1整数规划的可行解一定是线性规划松驰的可行解

线性规划松驰的最优解的值是0-1整数规划最优解的值的下界
对线性规划的解中每个带小数的数四舍五入成０或１
加权最小顶点覆盖：2-近似算法

随机算法

最大可满足性问题（Maximum satisfiability）

数学期望：2-近似
加权最小顶点覆盖：

局部搜索

local search

最大割问题 Maximum Cut

图G = ( V, E )，找到连接划分V1中的点与V2中的点的边的数目最大的划分

给定初始可行解，迭代寻找优于当前解的相邻解（neighbor solution）
2-近似算法(?)

启发式算法

定义

编码方式：
- 背包问题和指派问题：0-1编码
- TSP问题和调度问题：自然数编码
- 连续函数优化：实数编码表示法等

邻域搜索 Neighborhood Search

基本原理：基于贪心思想, 持续地在当前解的邻域中搜索, 直至邻域中再也没有更好的解, 也称为爬山启发式算法
特点：
- 易理解易实现, 具有很好的通用性,
- 但搜索结果完全依赖于初始解和邻域的结构，只能搜到局部最优
改进：变邻域搜索算法(Variable Neighborhood Search, VNS)

在多个邻域结构间进行交替搜索，在集中性和疏散性之间达到很好的平衡

禁忌搜索 Tabu Search

标记对应已搜索到的局部最优解的一些对象（对应移动s(x)得到x*）

通过引入一个禁忌表和相应的禁忌准则来避免局部迂回（移动s的重复）

通过渴望准则来挽救某些被禁忌的相对优化解（一般是小于(s,x)历史最优解）
对局部邻域搜索的一种扩展，可以很好地实现全局寻优
改进：
- 主动禁忌搜索算法：
  利用增大/减小调节系数 动态调整禁忌表长度：出现重复解增大长度，连续num_dec次未出现减小长度
  逃逸机制：出现重复解次数超过num_esc，随机移动避免循环
- 并行禁忌搜索算法：对算法的初始化、参数设置、通信方式等方面实施并行策略

模拟退火算法 Simulated Annealing

模拟热力学中退火过程能使金属原子达到能量最低状态的机制，通过模拟的降温过程按波尔兹曼方程计算状态间的转移概率来引导搜索
基于Metropolis准则的邻域移动
- 无条件移动（同邻域搜索）：如果新解的目标函数值小于当前解的目标函数值 (新状态的能量小于当前状态的能量)
- 有条件移动（新规则）：否则，依据一定的概率（和温度指数相关的波尔兹曼方程）进行有条件移动
内循环：在每一温度, 循环迭代相同的次数 or 根据温度𝑇𝑘来计算内循环次数

外循环：用降温函数控制温度的下降方式
特点：
- 具备良好的全局搜索能力，最终解逼近全局最优解，对初始解的依赖较低

遗传算法 Genetic Algorithm

基本原理：遗传算法是一种基于群体寻优的方法，算法运行是以一个种群在搜索空间进行搜索，根据具体问题构造恰当适值函数，根据适应值的大小不断选择和繁殖
过程：
- 初始：初始种群是随机产生的
- 选择：个体 $i$ 适应值 $f_i$ 被选中概率 $p_i=\displaystyle\frac{f_i}{\sum f_i}$
- 遗传算子(GeneticOperator)
  - 交叉(Crossover)
    - 单切点交叉：在双亲的染色体上随机地选择一个断点, 将断点的右段互相交换
    - 双切点交叉：随机选择两个切点，将两个切点中间的子串分别交换
  - 变异(Mutation)
    
    按照变异概率𝑃𝑚(5%以下) 任选若干基因位改变其位值
- 停止准则：最大代数 𝑁𝐺 (Number of Max Generation)
编码：染色体与优化问题的解对应
特点：
- 同时处理群体中的多个个体，减少了陷入局部最优解的风险，算法本身易于并行化

蚁群算法 Ant Colony

基本原理：采用人工蚂蚁的行走路线来表示待求解问题可行解，每只人工蚂蚁在解空间中独立地搜索可行解，以相对较大的概率选择信息素较多的路径

粒子群优化算法

基本思想：一个由m个粒子组成的群体在D维空间中以一定的速度飞行

每个粒子在搜索时考虑自己搜索到的历史最好点和群体内 (邻域内)其他粒子的历史最好点，进行位置 (状态或解) 的变化
过程：初始化为一群随机粒子

每一次迭代中，粒子通过跟踪两个“极值”来更新（位置、适应值、速度）
- 个体极值：粒子本身所找到的最优解
- 全局极值：整个种群目前找到的最优解
特点：公式简单，待定系数少，可用来解实优化

语言

C++

指针

指针

指针表示的是数据的存储地址，而非数据本身

数组名可以看做是一个指针常量，指向数组起始地址（第一个元素地址）

函数名表示的是一个函数的可执行代码的入口地址，也就是指向该函数可执行代码的指针
二维数组 a[2][3]

列指针 *a + j，第 i 行 j 列元素*(*a + i*3 + j)

行指针 a + i，第 i 行 j 列元素*(*(a + i) + j)

名称	例子	含义
指针函数	`char strstr(char s, char *s1);`	该函数返回一个指针
函数指针	`int (*f_name) (…);`	指向一个函数(返回int)的指针
指针数组	`char *a[N]`	数组的元素是指针
数组指针	`char (*a)[N]`	指向一个数组首地址

STL

名称	vector	queue	stack	set	map	priority_queue	list
含义	动态大小数组	队列，先进先出	栈，先进后出	存储唯一元素，二叉搜索树	key-value映射	相当于大顶堆	双向链表
索引	at(); operator []; front(); back();	front(); back();	top();	count(); find();	at(); operator []; count(); find();	top();	front(); back();
插入删除	push_back(); pop_back(); v1.insert(v1.end(), v2.begin(), v2.end()); v.erase(v.begin() + i);	push(); pop();	push(); pop();	insert(); erase();	insert(); erase();	push(); pop();	push_front(); pop_front(); push_back(); pop_back();
Iterator	begin(); end(); rbegin(); rend();			begin(); end(); rbegin(); rend();	begin(); end(); rbegin(); rend();		begin(); end(); rbegin(); rend();

JAVA

tbc...

posted @ 2024-05-17 19:15 Beatrix_Y 阅读(1572) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 北航研究生《矩阵理论》期末复习整理与2024考题记录

· 【软工】week6-结对编程作业-最长英语单词链

· leetcode之二叉树

· 数据结构与算法（AaDS）复习知识点

· 2024网安数据结构恐龙提纲

公告

昵称： Beatrix_Y
园龄： 4年2个月
粉丝： 5
关注： 3

+加关注

2025年3月

日

一

二

三

四

五

六

Beatrix_Y

北航研究生《算法设计与分析》期末复习整理

数据结构

二叉树

线索二叉树(Threaded Binary Tree）

二叉查找树(Binary Search Tree, BST）

平衡二叉树(Adelson-Velskii and Landis, AVL）

堆(Heap)

哈夫曼树(Huffman Tree）

优先队列(Priority queue）

多叉树

B树(Balanced Tree)

2-3树

B+树

图

最小生成树

最短路径问题

欧拉图

哈密顿图

排序

算法

常见题型

双指针(面试)

随机算法

减治分治变治

回溯法

贪心算法

动态规划

最优排序规则

最长公共子序列

矩阵链相乘

最短路径问题

有向图的传递闭包

最优二叉查找树问题

01背包问题

矩阵快速幂

分支定界算法

时间复杂度

上下界符号

NP问题

近似算法

定义

贪心算法

最小顶点覆盖

最小集合覆盖

最小工期分配

旅行商问题TSP

背包问题

线性规划

随机算法

局部搜索

启发式算法

定义

邻域搜索 Neighborhood Search

禁忌搜索 Tabu Search

模拟退火算法 Simulated Annealing

遗传算法 Genetic Algorithm

蚁群算法 Ant Colony

粒子群优化算法

语言

C++

指针

STL

JAVA

公告

常用链接

我的标签

随笔档案 (13)

阅读排行榜

推荐排行榜