面向对象课程第一单元总结

第一次作业

程序结构

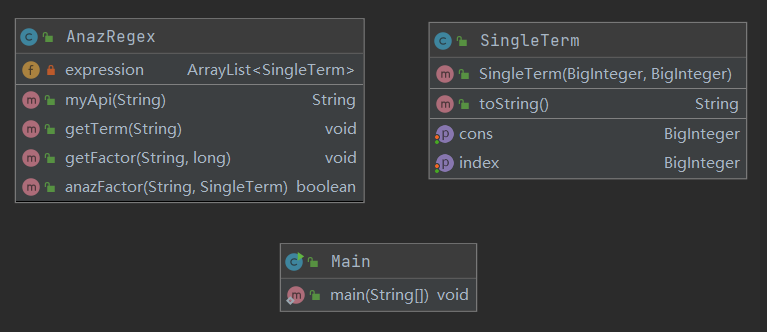
实质上只有两个类，\(SingleTerm\)是标准项（即把所有项表示成\(cons*x^{index}\)的形式），\(AnazRegex\)用来解析字符串，采用正则表达式匹配。

在\(AnazRegex\)中将形式化表述中的表达式->a|表达式+b，转化为读入a，循环matcher.find()读入b（和后面递归下降的消除左递归实际上原理上是相同的）。

在合并同类项的时候，将指数相同的项的系数相加，并按照指数从大到小对\(SingleTerm\)组成的\(ArrayList\)进行排序，输出具有唯一性。

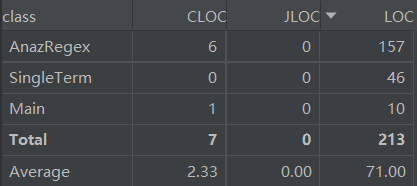
度量情况：

可以看出，主要的复杂度都集中在两个类，实际上五个比较复杂的方法中，三个是在解析字符串，一个是主要操作控制（调用解析字符串方法+合并同类项+排序+求导），一个是重写标准项的toString()方法

结论是正则表达式匹配比较复杂，需要优(chong)化(gou)

bug情况

未被别人/强测hack

采用了Generex库根据正则表达式自动生成字符串，注意需要去maven库下载依赖

由于我的输出具有唯一性，可以直接将别人的输出读入再输出进行.equals()，如果没有成功读入就是我的正则匹配错误或者对方格式错误，如果两个结果不一致则输出信息，否则一直运行即可。

我们房间比较风平浪静，我跑了几十万个点（数据五位数，每个项10+个因子，一共20+个项），只找到一个人的bug（可能还是同质bug）

心得体会

正则表达式写的过于复杂，改变要求几乎要重新写，并且很容易出错（所以第二次重构了）

Generex随机数据+唯一性输出是个偷懒的方法，还是需要抽时间学习评测机

第二次作业

程序结构

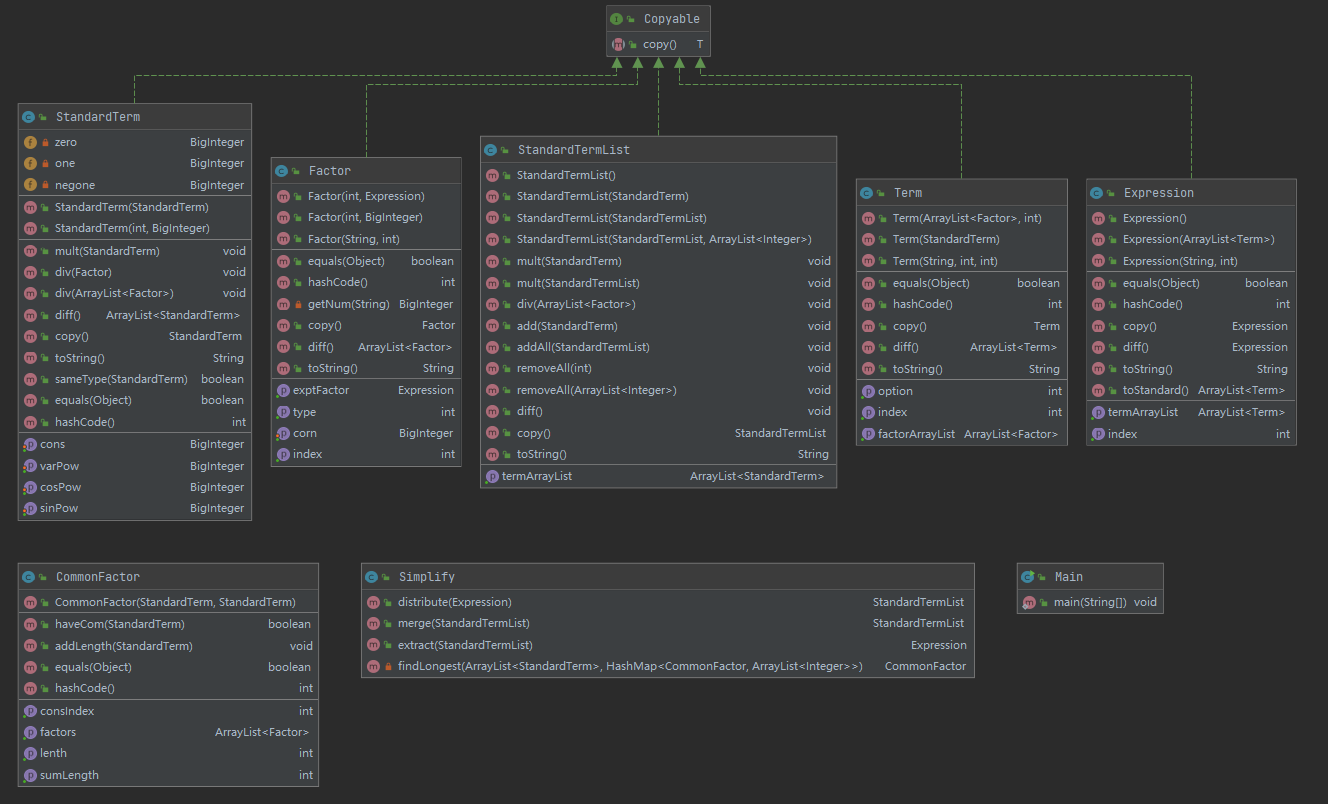
这次的类除了主类Main外，分为两种，一种是递归下降法读出的表达式、项、因子，一种是用于优化的类以及标准项、标准项List、公因式

由于优化输出采用了拆分所有括号+合并同类项+递归提取公因式，并且涉及到有嵌套表达式因子的项和标准项\(const*x^{exp}*sin(x)^{exp}*cos(x)^{exp}\)之间的转换，形式看起来会比较复杂

其中Copyable是用于deep copy的接口

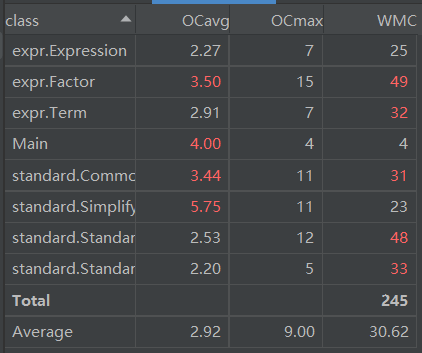
可以看到，类和方法的复杂度都偏高（但是还是符合checkstyle要求的）

优化长度

考虑到按人的思维进行多项式化简时，先把所有项拆开，再因式分解逐个合并，我的代码也采取了这种方式，即先提取公因式（包括常数因子的最大公因式），用一个keymap存储这些公因式和对应的标准项，找到能节省长度最大的公因式

公因式节省长度计算：设公因子长度为\(l\)，因子个数为\(n\)，则节省总长度\(sumLength=(l+1)*(n-1)-2-\Sigma(a_i+1)\)，其中\((l+1)*(n-1)\)表示省去的公因子以及乘号数目，\(-2\)表示减去增加的左右括号，如果第\(i\)项的常数因子除以公因式常数因子的值\(c_i\)不为1，则\(a_i\)为数字\(c_i\)的长度，否则\(a_i\)为-1。查找最佳因式分解方式即寻找\(sumLength\)最大值，直到没有\(sumlength>0\)的组合，将剩下所有标准项再转回\(factor\)组成的\(ArrayList\)，得到项和表达式输出。

按这个方式，middle-data-3的长度能缩小到150

bug情况

未被别人/强测hack，也没有成功找到别人的bug

但是后来自己查出来一个bug，就是在对字典遍历的时候，把entry.getkey()放到另一个函数的方法里，被改变了，导致被改变的key又访问了一次

教训：尽量不要在遍历中更改，尽量不要直接对方法传入参数进行更改(copy一下)

重构经历

研讨课上听了dhy和wjy两位大佬的分享，决定彻底重构采用递归下降法，我的实现架构如下：

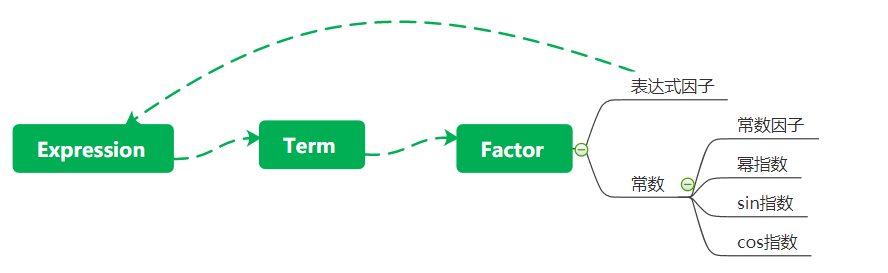
即Factor中只需要存表达式因子exprFactor，常数cons和type(代表cons的种类)

Expression递归拆括号获取标准项StandTerm：

定义标准项之间的乘法，没有表达式因子则逐个乘公共项，有表达式因子则递归将表达式因子转化为标准项List，将其中的每个标准项乘公共项再求和，得到新的公共项

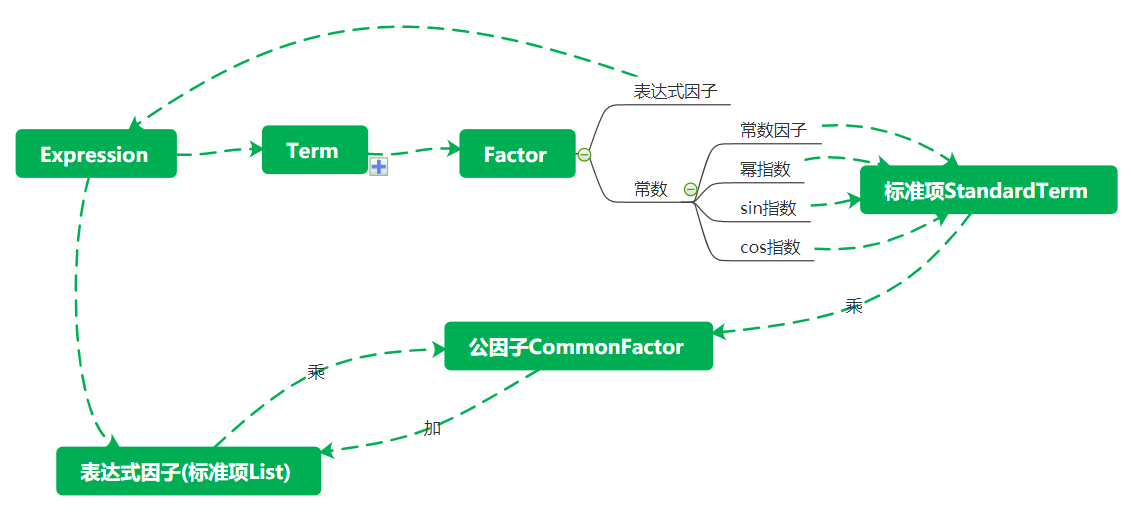
心得体会

1. 中间因为把equals方法定义为类型相同而不是完全相同，还使用了Arraylist的removeAll方法，出现了很多问题

2. 以及以后优化改一部分就交一个优化过的稳定版，这次作业由于担心达到10次的限制一直不敢提交，导致最后稳定版只有拆分了所有括号的版本，完全没有合并同类项，性能分很受影响

3. 研讨课十分有用，大佬的分享给了我很多启发，%%%

第三次作业

程序结构

延续了第二次作业的架构，递归下降方面只是微调，每个类和方法的定义构造上也都差不多。

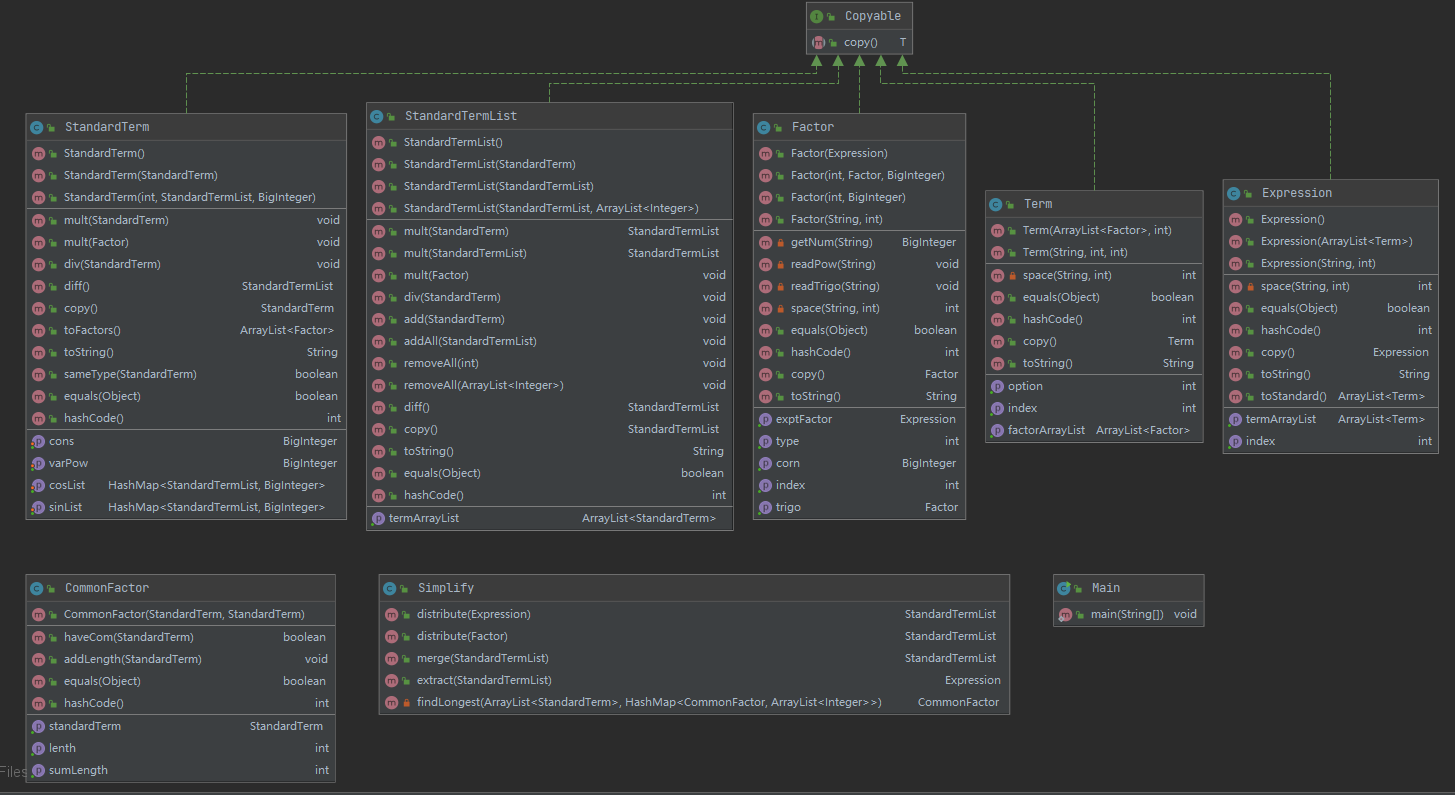
但是由于递归拆分括号的时候三角函数内的括号需要独立地递归拆分，标准项中的存储需要增肌sin和cos的因子的列表，变动比较大，因子和标准项的存储形式也没有原来简洁。

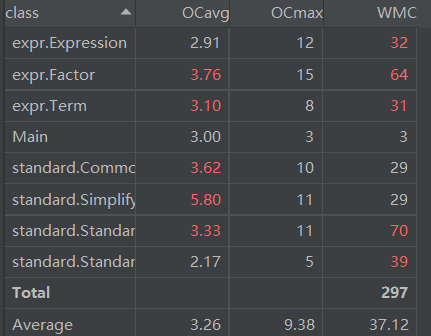
bug情况

主要是格式方面的问题

输入格式：只判断了是否有多余右括号，未判断缺少右括号

输出格式：主要是由于三角函数内为因子

(1) 在\(hw2\)中采取二次幂因子改为\(x*x\)输出，会导致因子变成表达式，在三角函数中如果不增加一层括号就是格式错误

(2) 在\(hw2\)中采取因子是0则toString返回 “” 的方式，只保证整个表达式不为 “”，可能会输出sin()

心得体会

1. 一开始由于没有认真读题，以为三角函数内是表达式，三级函数的括号就是表达式因子的括号，导致做了两倍\(hw2\rightarrow hw3\)的工作量，最重要的是一开始考虑都是基于三角函数内套表达式的，后续的很多错误都是因为没有扭转过来
2. 一定要记得不可变类的运算结果是返回一个新实例！直接a.multiply(b)的错误出现太多次了