码垛机器人
基本概念
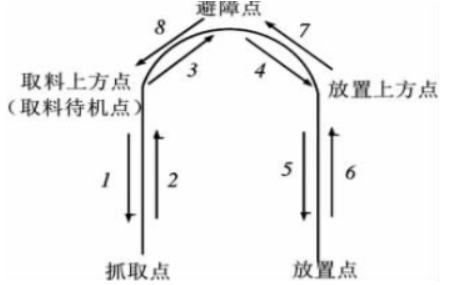
路径描述
抓取点，转向点，避障点，下降点，码放点
方程
码垛机器人力臂由多关节组成，自由度为各关节旋转角度
动力学方程：对每个关节分析力矩，相邻关节的作用力和机械臂重力形成的力矩
约束：(1)关节速度初末为零 \(v_n(0)=v_n(t_0)=0\)
(2)相邻关节间位移、速度、加速度连续
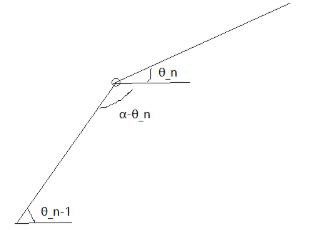
(3)相邻关节角度关系 \(\theta_n = \theta_{n-1}+\alpha_{n-1}-\pi\)
\(\Rightarrow\)运动学方程
需求
轨迹拟合
笛卡尔空间直线运动：
常见两直线段过渡方式：可控加速度转换段，圆弧，有理二次参数曲线
关节空间运动：
用\(l_i、\theta_i\)表示，其中\(i=1,2,3,…,n-1\)
关节空间轨迹计划方法：加减速曲线法，抛物线过渡法，多项式法
多项式法存在平均速度不高及多次加减速，抛物线过渡法可能会产生加速度突变
重复精度
定位点的精确度
速度
保证功率小于上限的前提下，速度尽可能快
稳定性
速度最快的情况下不会损害货物
优化
目前已有优化方向和一些思考：
运动轨迹
(1) 空间运动规划：
笛卡尔空间直线运动设计连接抓取点和码放点的机械手抓轨迹，再通过关节空间运动分析得到每个关节的广义位置
缺点：分别规划关节和抓手，在笛卡尔空间直线运动规划中，把多关节组成的码垛机器人看成单自由度机器人，没有考虑自由度的影响，在躲避障碍的过程中缺乏灵活性
(2) 遗传算法(Genetic Algorithm)：
目标函数：平均速度最大，加速度最小（高效&稳定）
约束：最大速度，初末速度为0，最大加速度，关节运动牵连(即位置、速度、加速度连续)，障碍物位置
对于非线性约束最优化方程组进行遗传算法求解：
是把实际问题中可能潜在的解作为个体，经过一定数目个体的基因编码形成一个种群，按照生物进化原理，根据目标函数的大小进行个体的选择(selection)、组合交叉(crossover)和变异(mutation)，通过模拟生物进化的过程，逐步产生新的解集，直至产生满足收敛条件的最优解。
缺点：遗传迭代过程中需要选择的参数较多，且参数对结果影响很大，但是没有参数选择规范，几乎完全依赖于经验
(3) 蚁群算法(Ant Colony Optimization)：
路径：起点、终点确定，有多个障碍
原理：蚂蚁的行走路径表示待优化问题的可行解，整个蚂蚁群体的所有路径构成待优化问题的解空间。随着时间的推进，较短的路径上累积的信息素浓度逐渐增高，选择该路径的蚂蚁个数也愈来愈多。最终，整个蚂蚁会在正反馈的作用下集中到最佳的路径上，此时对应的便是待优化问题的最优解。
侧重点：躲避障碍物的最优路径
缺点：正反馈使得初态非常重要，存在局部最优问题(即次优解占优势)；只关注了障碍物而忽略其他约束，以及未考虑码垛机器人的多自由度
速度分配
理想状态下加速到最大速度立刻减速，初末速度为0，平均速度为\(\frac{1}{2}v_{max}\)
实际受到最大功率和稳定性的限制，通常为梯形加减速
码垛排样
改变码放点位置，自适应排样
优点：(1)制定排样规则，使得操作具有重复性，大大降低复杂度
(2)改变码放点位置，使得根据抓取点、码放点、障碍物及约束计算的路径得到进一步优化
我认为本项目主要可选择的优化方向为有障碍的最优运动轨迹算法，以及码垛自适应排样算法
