快排-归并-堆排序
概述
排序算法算是最经典的算法了，只要你学习算法，就永远也离不开他，常用的排序算法有：
- 冒泡排序
- 插入排序
- 希尔排序
- 桶排序
- 计数排序
- 计数排序
- 快速排序
- 归并排序
- 堆排序
这些排序大致特点如下：
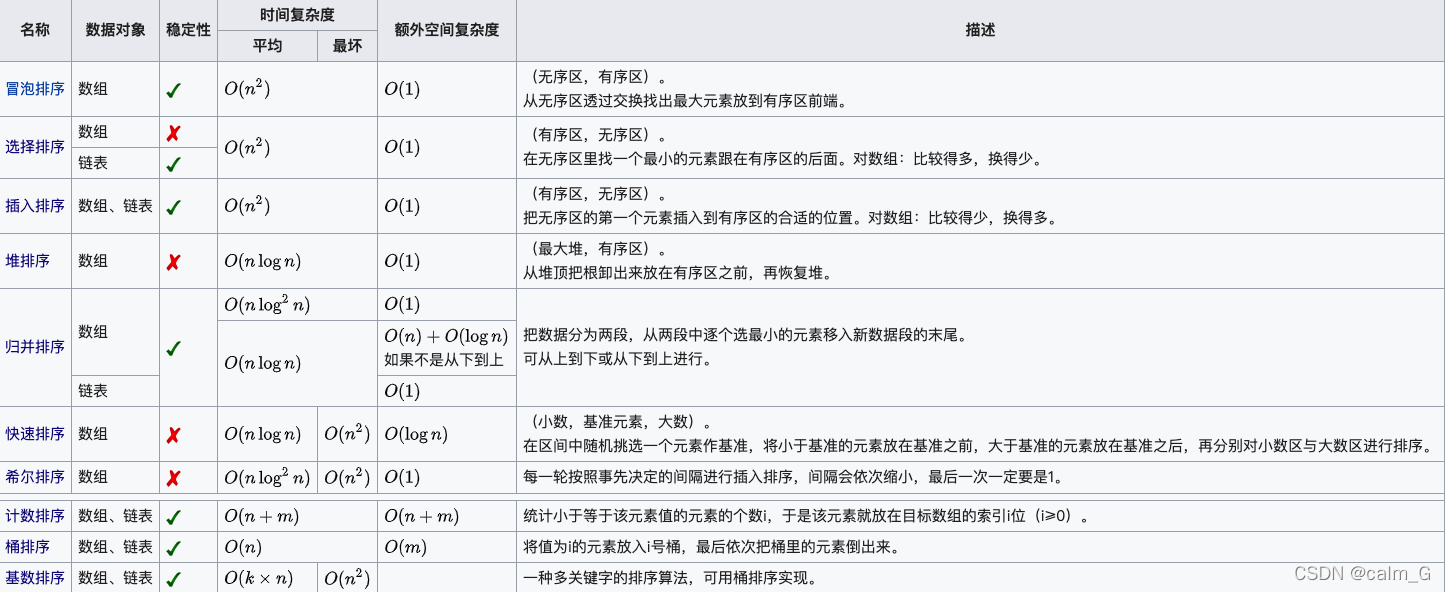
其中最重要，也最复杂的三种排序，分别是：
- 快速排序
- 归并排序
- 堆排序
一. 快速排序
1. 大致思路
核心：每一次选定一个基准值（一般选择第一个），通过前后比较，比这个值小的放在它前面，比它大的放在它后面，一轮比较过后，这个值就在他应该在的位置了，且前面的值都小于他，后面的值都大于他。图解如下（挖坑法）：
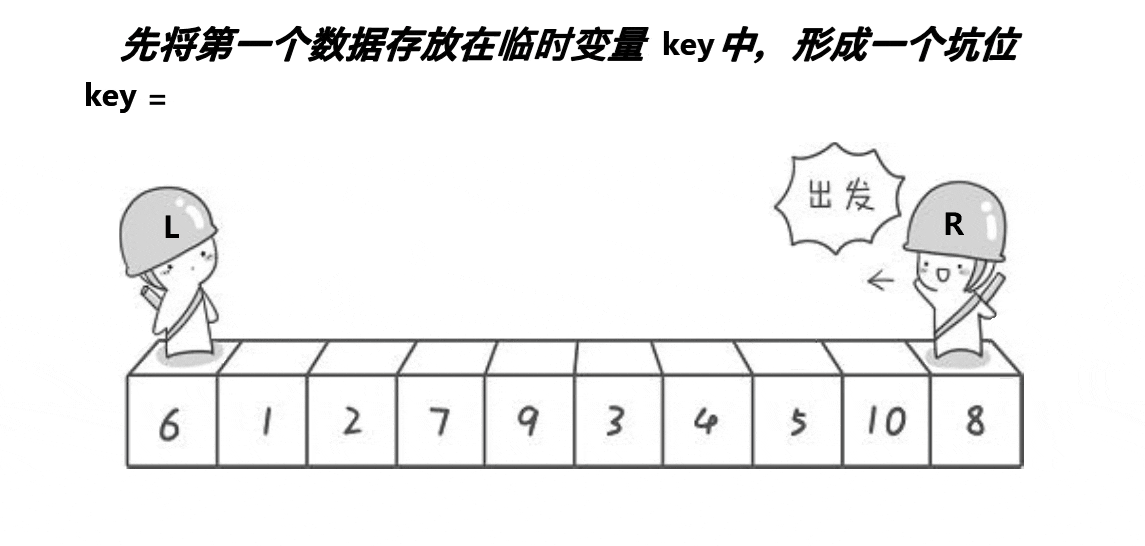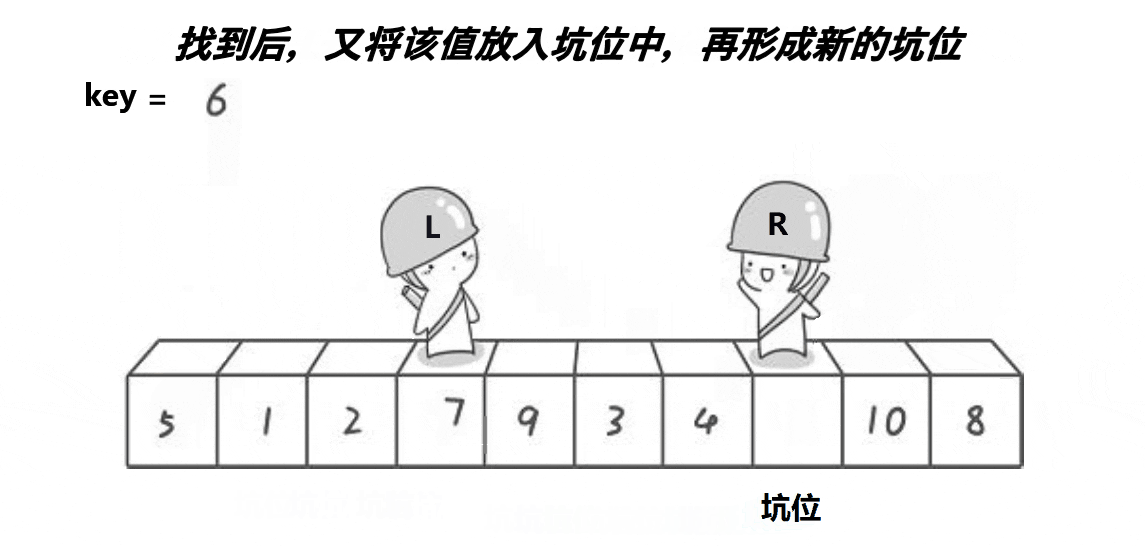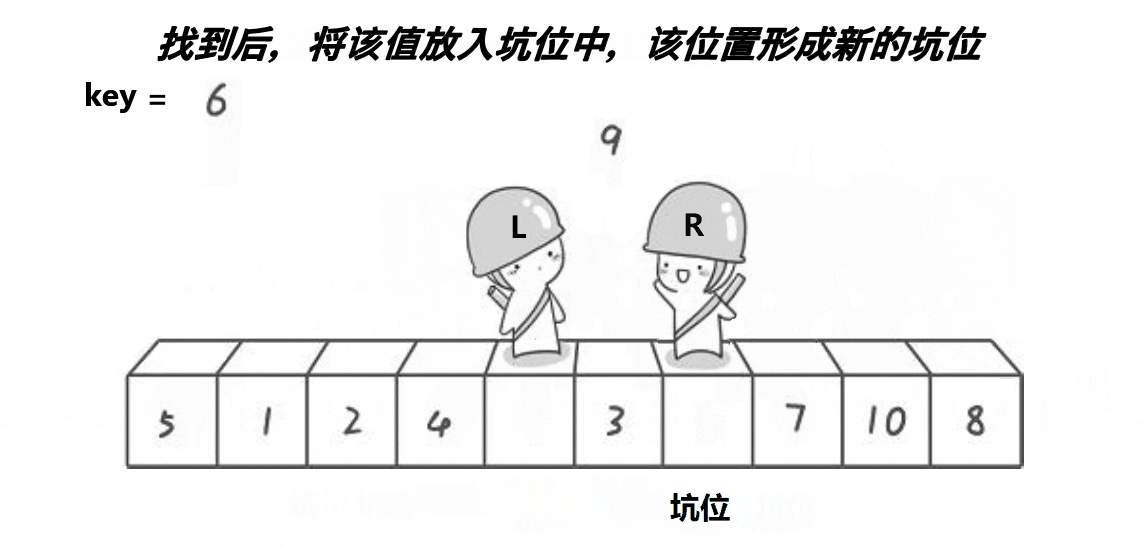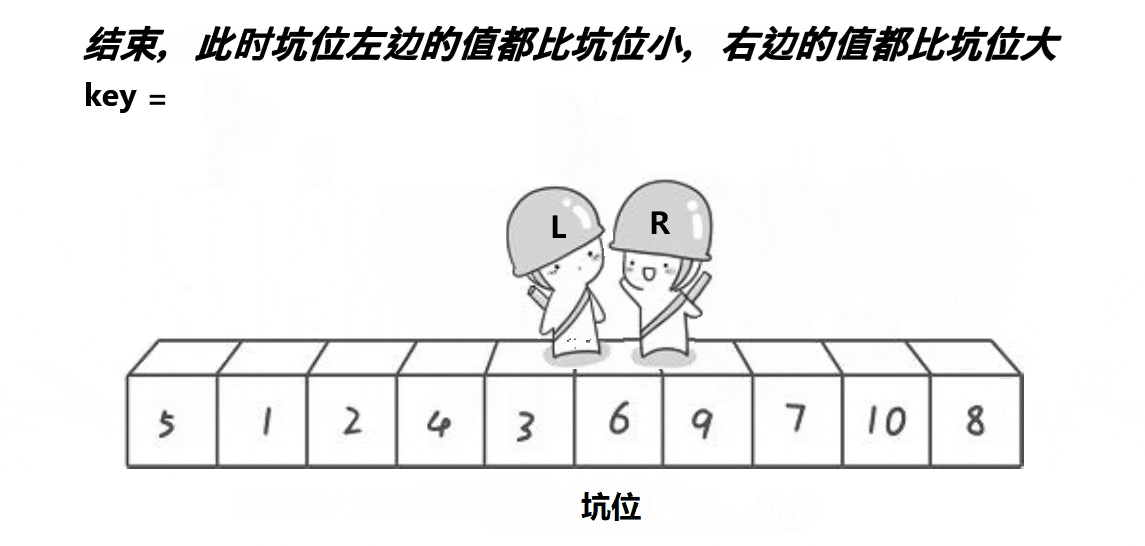
步骤：
- 选出一个基准（一般选第一个）作为标准值flag，这个地点出现坑位hole。
- 定义一个L指针和一个R指针，指向要排序部分的最左、最右端。
- 随后R先向前扫描，如果R指向的值小于flag，那么用R指向的值填补hole，hole=R，R停止移动。
- L开始向后扫描，如果L指向的值大于flag，那么用L指向的值填补hole，hole=L，L停止移动。
- 重复3、4步，直到L==R，此时L和R都指向hole，将标准值填入hole中。
上述步骤完成了一轮循环。每一轮循环，最后hole都会将当前要排序的数组段分割成两部分，随后还需要对这两部分分别分别进行排序。显然，我们可以使用递归的方式。
2. 代码实现
// 快速排序：采用挖坑法
void change(int*, int *);
// 单次排序，将标志节点(这里采用首节点)存放到对应的位置
int partSort(int arr[], int begin, int end){
// 找到基准点
int hole = begin;
int key = arr[begin];
int i = begin;
int j = end;
while(i < j){
while(i < j && arr[j] >= key){ // 注意左右遍历时要保证left < right
j--;
}
arr[hole] = arr[j];
hole = j;
while(i < j && arr[i] <= key){
i++;
}
arr[hole] = arr[i];
hole = i;
}
// 此时左右指针相遇，都指向一个坑，将最开始保存的首节点的值存在这里
arr[hole] = key;
return hole;
}
// 递归实现快速排序
void quickSort(int arr[], int begin, int end){
if(begin >= end) return;
int hole = partSort(arr, begin, end);
quickSort(arr, begin, hole - 1);
quickSort(arr, hole + 1, end);
}
二. 归并排序
1. 大致思路
核心：归并排序的核心在于利用了二分的思维，将数组不断切割，直到切割出的数组长度为1，此时切割出的数组自然有序，然后再让这些有序数组合并，不断回溯、合并，直到所有数据排序完成
图解：
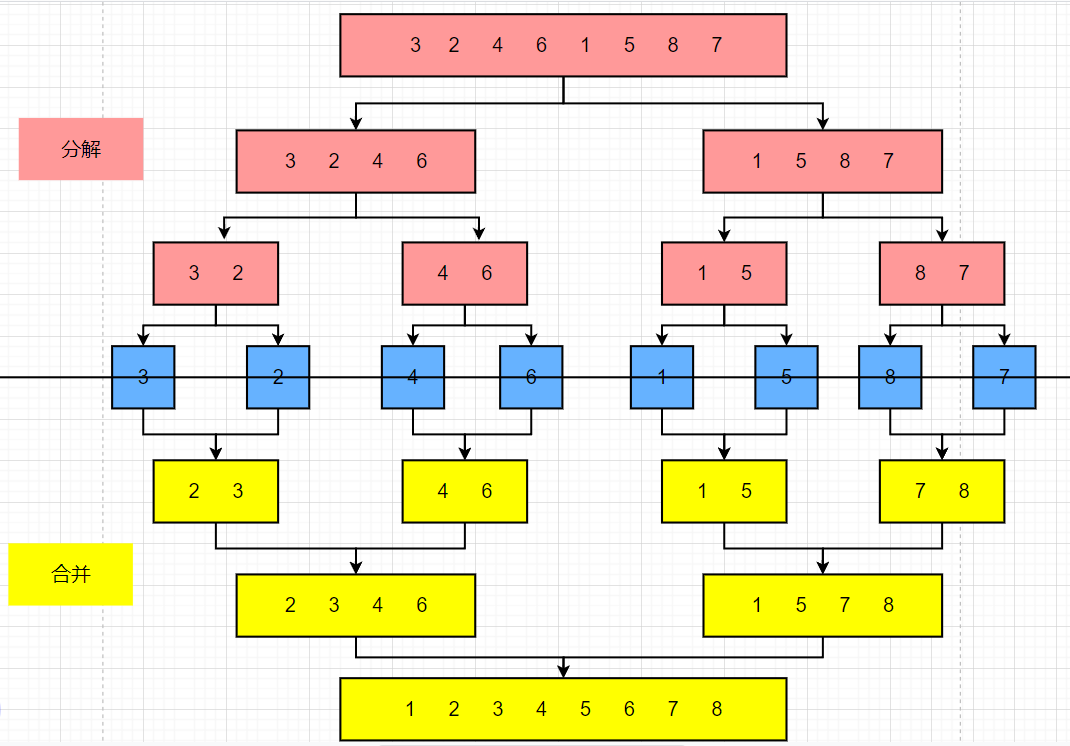
2. 代码实现
// 合并两个有序的数组：其中sourceArr为原数组，而tempArr为辅助数组
void merge(int sourceArr[], int tempArr[], int begin, int mid, int end){
int index = begin;
int i = begin;
int j = mid + 1;
while(i <= mid && j <= end){
if(sourceArr[i] <= sourceArr[j]){
tempArr[index] = sourceArr[i];
i++;
} else{
tempArr[index] = sourceArr[j];
j++;
}
index++;
}
while( i < mid+1 ){
tempArr[index++] = sourceArr[i++];
}
while( j < end+1 ){
tempArr[index++] = sourceArr[j++];
}
for(int var = 0; var <= end; var++){
sourceArr[var] = tempArr[var];
}
}
// 归并排序：递归实现
void mergeSort(int sourceArr[], int tempArr[], int begin, int end){
if(begin < end){
int mid = begin + (end - begin) / 2; // 防止int类型溢出
mergeSort(sourceArr, tempArr, begin, mid);
mergeSort(sourceArr, tempArr, mid + 1, end);
merge(sourceArr, tempArr, begin, mid, end);
}
}
三. 堆排序
1. 大致思路
堆：堆分为两种
- 大顶堆：所有的根节点大于子节点。
- 小顶堆：所有的根节点小于子节点。
所有堆都是一个完全二叉树，因此我们可以很简单的将他映射到一个数组上。
核心思路：堆排序的关键在于利用堆（这里以大顶堆为例），通过在逻辑上构建一个大顶堆（实际上是对数组进行调换），堆的根节点就是最大的值，随后将根节点和数组末尾的值替换，最大的数就被调换到数组的末尾了。随后将数组长度减一，然后对长度减一后的数组进行调整，让它再次符合大顶堆的定义，然后再次调换。如此往复，直到需要调整的数组长度变为1。
堆的构建：从最后一个非叶子节点开始，逐个向前遍历，直到根节点，都进行如下操作：
- 假设当前需要调整的节点为N，如果N大于它的左右孩子，那么返回，无需调整。否则，进行2。
- 如果子节点中的最大节点\(arr[c_{max}]>arr[N]\)，那么调换二者的值。然后用\(c_{max}\)替换N，回到步骤1。
堆的调整：此时堆已经构建完毕，因此如果令堆的顶M和最后一个节点交换N，随后删除M，我们需要对新的顶节点N进行判断，方式很简单，和堆的构建右异曲同工之妙：
- 假设当前需要调整的节点为N，如果N大于它的左右孩子，那么返回，无需调整。否则，进行2。
- 如果子节点中的最大节点\(arr[c_{max}]>arr[N]\)，那么调换二者的值。然后用\(c_{max}\)替换N，回到步骤1。
2. 代码实现
// 堆排序：构造大顶堆，对数组进行从小到大排序
void swap(int* a, int* b){
int temp = *a;
*a = *b;
*b = temp;
}
// 对传入的父结点进行排序(调用时会从最后一个非叶子节点开始调用，一直到根节点)
void headAdjust(int* arr, int len, int node){
// 左孩子的下标
int l_child = node * 2 + 1;
int c_max = l_child; // 记录子孩子中最大的一个
if(l_child >= len) // 说明传入节点没有子节点
return;
// 找到子结点中最大的一个
if(l_child + 1 < len && arr[l_child + 1] > arr[l_child]){
c_max = l_child+1;
}
// 判断是否需要交换位置
if(arr[c_max] > arr[node]){
swap(&arr[c_max], &arr[node]);
headAdjust(arr, len, c_max);
}
return;
}
// 开始排序
void headSort(int* arr, int len){
// 首先构建大顶堆
for(int i = len/2+1; i >= 0; i--){
headAdjust(arr, len, i);
}
while(len >= 1){
// 将大顶堆的堆定和末尾的数据交换，此时最大的值就移动到了数组最后
swap(&arr[0], &arr[len-1]);
// 此次修改导致大顶堆混乱，需要从新交换过去的根节点重新构建大顶堆
len--;
headAdjust(arr, len, 0);
}
}
