买卖股票的最佳时机III Best Time to Buy and Sell Stock III
##### Best Time to Buy and Sell Stock III
买卖股票的最佳时机III
题目
题意
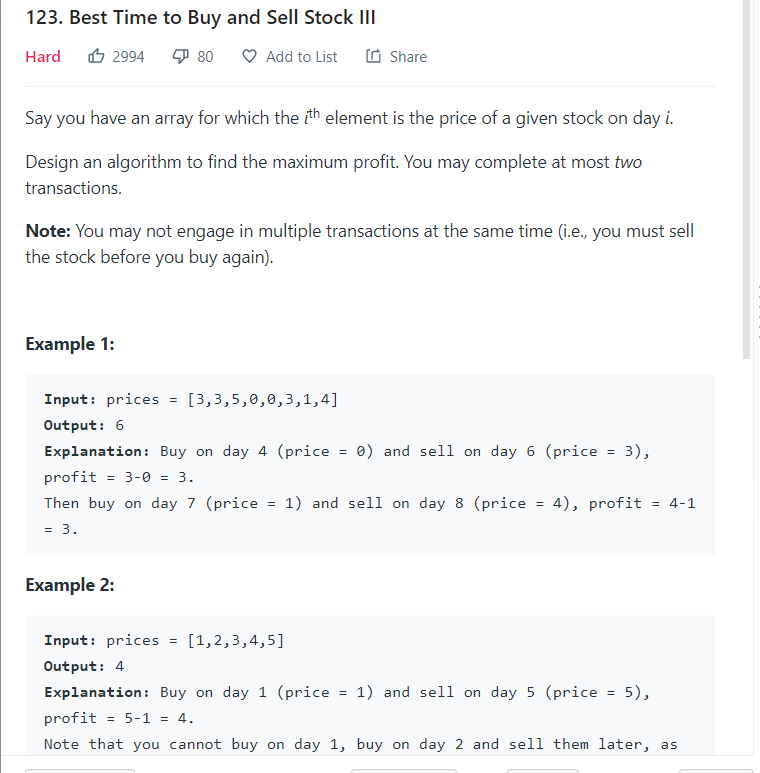
有两次买入和卖出股票的机会,求所获收益的最大值(第二次买入时需卖出第一次买入的股票)
分析
股票买卖问题的升级版
相较于基础问题股票买卖限定了两次购买 无法立即得出解题方法, 需要仔细分析
思路一
因为题目要求最多两次买卖,所以我们将序列分为两段,前一段为第一次买卖,后一段为第二次买卖
按股票买卖一中的方法先遍历序列,当我们每次找到一个新的值能使第一次买卖获利变大后,计算该值后面的序列进行买卖所能获得的最大收益,将两次收益合并为总收益
//伪代码
for(int i=0;i<n;i++){
minPrices=min(minPrices,prices[i]); //当前发现的最小值
if(prices[i]-minPrices>maxProfit){
maxProfit=prices[i]-minPrices; //更新第一次收益
allProfit=max(allProfit,maxProfit+getProfit(prices,i+1,n)) //getprofit为获得第二次收益
}
}
P.S
关于为什么每次是找到新的第一次收益才去找第二次的值
因为随着序列的遍历,我们第二段序列是越来越短,第二次的收益也是越来越小的
所以在第二段收益不再变大的情况下,只有第一次收益变大才会使总收益变大
#python代码
class Solution(object):
def getProfit(self,a):
if len(a)==0:
return 0
m=a[0]
maxn=0
for i in range(len(a)):
if(a[i]<m):
m=a[i]
if(a[i]-m>maxn):
maxn=a[i]-m
return maxn
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
allProfit=0
if len(prices)==0:
return 0
minPrices=prices[0]
maxProfit=0
for i in range(len(prices)):
if(prices[i]<minPrices):
minPrices=prices[i]
if(prices[i]-minPrices>mam):
maxProfit=prices[i]-minPrices
allProfit=max(allProfit,maxProfit+self.getProfit(prices[i+1:]))
return allProfit
方法二
该方法为通用解法
该系列题目中有 一次 两次 无限次等买入
我们认为题目是给了k次买入机会
这样的话我们需要用动态规划的方法来仔细拆解该问题
状态
该问题共三个状态 面对的股票、当前是否有买入机会,当前是否持有股票
整体来说为三维\(dp\)问题
\(dp[n][k][p]\) 表示面对第n天的股票,在拥有k次买入机会时,目前可买入状态为p时所获得的收入最大值(p==0代码未买入状态 p ==1 代码买入状态)
三维\(dp\)有些复杂
我们可以通过拆解买入状态来提高代码的可读性
令\(dpBuy[n][k]\) 为处理完第n天股票时 买入状态下的最大收益
\(dpSell[n][k]\) 为处理完第n天股票时,卖出状态下最大收益
则我们需要的答案为 \(dpSell[n-1][k]\) n为天数 k为购买次数
状态转移方程
当我们拥有上述两者状态时
对待每一天的股票
\[dpSell[i][j]=max
\begin{cases}
dpSell[i-1][j] &\text 此次不卖出 \\
dpBuy[i-1][j]+prices[i] &\text 卖出
\end{cases}
\]
\[dpBuy[i][j]=max
\begin{cases}
dpBuy[i-1][j] &\text 此次不买入\\
dpSell[i-1][j-1]-prices[i] &\text 买入
\end{cases}
\]
核心代码为
for(int i=1;i<n;i++){
for(int j=1;j<=k;j++){
dpSell[i][j]=max(dpSell[i-1][j],dpBuy[i-1][j]+prices[i]);
dpBuy[i][j]=max(dpBuy[i-1][j],dpSell[i-1][j-1]-prices[i]);
}
}
完整代码为
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n=prices.size();
if(n==0){
return 0;
}
int k=2;
int **dpSell=new int *[n];
for(int i=0;i<n;i++){
dpSell[i]=new int[3];
}
int **dpBuy=new int *[n];
for(int i=0;i<n;i++){
dpBuy[i]=new int[3];
}
for(int i=0;i<n;i++){
for(int j=0;j<=k;j++){
dpSell[i][j]=0;
dpBuy[i][j]=0;
}
}
for(int i=0;i<=k;i++){
dpSell[0][i]=0;
dpBuy[0][i]=-prices[0];
}
for(int i=1;i<n;i++){
for(int j=1;j<=k;j++){
dpSell[i][j]=max(dpSell[i-1][j],dpBuy[i-1][j]+prices[i]);
dpBuy[i][j]=max(dpBuy[i-1][j],dpSell[i-1][j-1]-prices[i]);
}
}
// for(int i=0;i<n;i++){
// printf("%d ",dpSell[i][k]);
// }
return dpSell[n-1][k];
}
};



