LeetCode 1690. Stone Game VII 石子游戏 VII

#### LeetCode

1690. Stone Game V11

此题来源于2020.12.13 周赛第三题

题目

题意

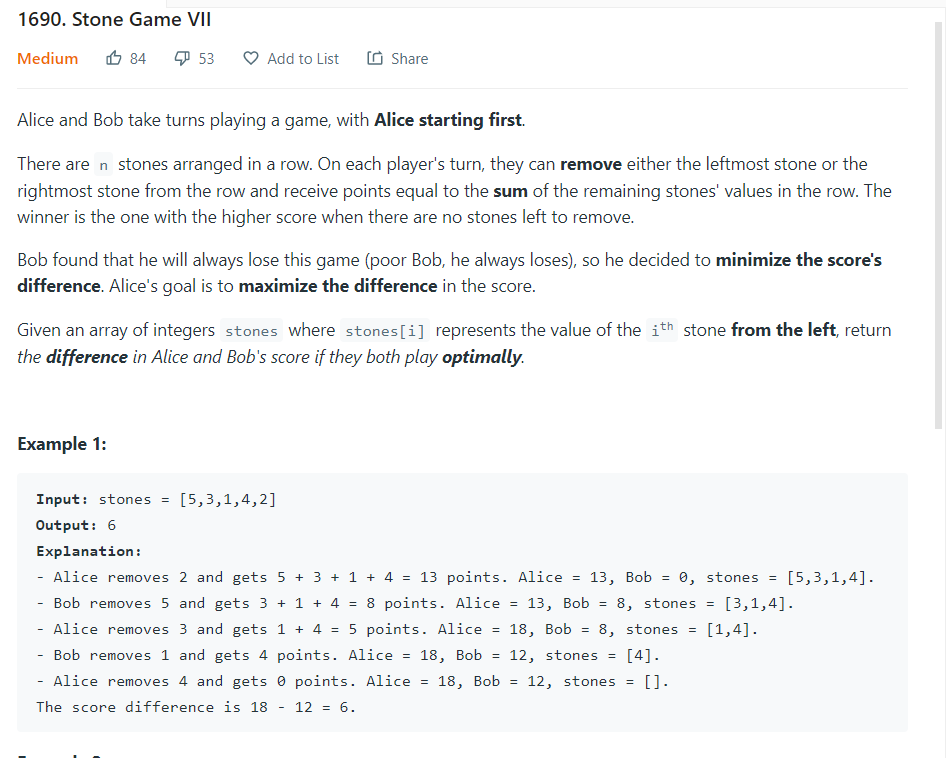
有从左到右排列整齐的n个石头，其重量分别为a[0....n] ， Bob和Alice分别按以下规则依次去将石头取出

1. 只能从剩余石头序列的最左或者最右选取石头取出
2. 每名选手在选取后获得序列中剩余石头的重量和的分数
3. Alice先手

很明显该游戏先手必胜，游戏过程中Bob会采取最佳策略去最小化与Alice分数的差值，同时Alice也会采取最佳策略去最大化分数差则

求 在双方都采用最优策略时 他们最终分数的差值

解析

通过分析题意我们可以认为这是一道动态规划题

规划的对象是该序列的连续子序列 到该序列

我们假设 \(dp[i][j]\) 为 面对序列\(Stones[i]\).... \(Stones[j]\) 时最终分数的差值

那么对于Alice来说 每次选择两遍那个能使分数差则更大的石头，即

\[dp[i][j]=max \begin{cases} dp[i+1][j]+Stones[i+1]+...+Stones[j] &\text 选取左边的石头\\ dp[i][j-1]+Stones[i]+...+Stones[j-1] &\text 选取右边的石头 \end{cases} \]

对于Bob来说，每次选择使分数差值最小的石头, bob得分会使分值差值变小

\[dp[i][j]=min \begin{cases} dp[i+1][j-Stones[i+1]-...-Stones[j] &\text 选取左边的石头\\ dp[i][j-1]-Stones[i]-...-Stones[j-1] &\text 选取右边的石头 \end{cases} \]

有了该状态转移方程可以 开始编写代码

#include<vector>
class Solution {
public:
    int stoneGameVII(vector<int>& stones) {
        
        vector<vector<int> > dp(stones.size()+1,vector<int>(stones.size()+1,0));
        int n=stones.size();
        vector<int>sum(n+1,0);
        sum[0]=0;
        for(int i=1;i<=n;i++){
            sum[i]=stones[i-1]+sum[i-1];
           // 使用前缀和减少运算过程a[i]到a[j]进行累加的操作
            //注意！！！ 此处的sum[i] 是a[0]+...+a[i-1] 并不包括 a[i], 如果包括a[i] 后续代码会访问越界
        }
            for(int j=1;j<n;j++){ //剩余石头个数
                for(int i=0;i<n-j;i++){  //选择起点
                    int k=i+j; //终点
                        
                    if((n+j-1)%2==0){ //判断轮到谁选取
                        dp[i][k]=max(sum[k+1]+dp[i+1][k]-sum[i+1],sum[k]+dp[i][k-1]-sum[i]);
                       // printf("Alice 取石子\n");
                    }else{
                        dp[i][k]=min(sum[i+1]-sum[k+1]+dp[i+1][k],dp[i][k-1]+sum[i]-sum[k]);
                        //printf("bob\n");
                    }                    
                }
            }
        return dp[0][n-1]; //返回最终值
    }
   
};

details

我们迭代中用的是剩余石头个数和起点作为迭代对象

因为我们规划的目标为长度为原石头数组长度且起始点和终点都为原石头数组的起始和终点 的值

故此处应该从这两个变量入手，从低到高进行迭代从而得到答案