棋盘覆盖问题可视化动图——python

#### 棋盘覆盖问题可视化动图——python

棋盘覆盖问题是一个经典的分治法解决的问题，具体内容可以参照以下博主的解析

棋盘覆盖算法解析

为了更好的理解该算法分治的过程

利用了python中的matplotlib库进行了该算法的可视化

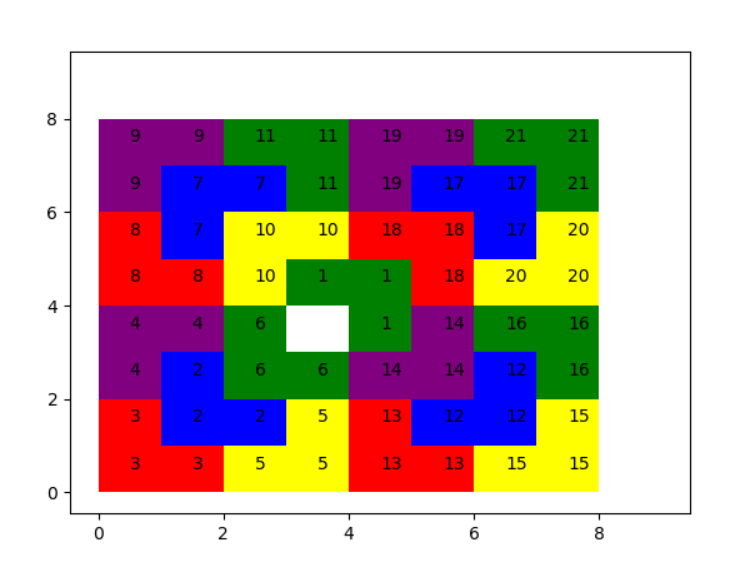
具体动画可复制代码在本地运行查看

import matplotlib.pyplot as plt 
import numpy as np 

count=0
color=['yellow','green','blue','red','purple'] #颜色数组


def fill(x,y,t):

    xx=np.linspace(x,x+1,10)
    yy=np.linspace(y,y,10)
    yy1=np.linspace(y+1,y+1,10)
    plt.fill_between(xx,yy,yy1,facecolor=color[t%(len(color))]) #填充
    plt.text(x+0.5,y+0.5,t) #添加文字
    plt.pause(1) #动态画图 参数为变化的时间
    pass 


def ChessBoard(tr,tc,dr,dc,size):
    if size==1:  #算法实现
        return 
    global count
    global Board 
    count+=1
    t=count
    s=size//2
    if dr<tr+s and dc<tc+s:
        ChessBoard(tr,tc,dr,dc,s)
    else:
        Board[tr+s-1][tc+s-1]=t
        fill(tr+s-1,tc+s-1,t)
        ChessBoard(tr,tc,tr+s-1,tc+s-1,s)
    
    if dr<tr+s and dc>=tc+s:
        ChessBoard(tr,tc+s,dr,dc,s)
    else:
        Board[tr+s-1][tc+s]=t
        fill(tr+s-1,tc+s,t)
        ChessBoard(tr,tc+s,tr+s-1,tc+s,s)

    if dr>=tr+s and dc<tc+s:
        ChessBoard(tr+s,tc,dr,dc,s)
    else:
        Board[tr+s][tc+s-1]=t
        fill(tr+s,tc+s-1,t)
        ChessBoard(tr+s,tc,tr+s,tc+s-1,s)

    if dr>=tr+s and dc>=tc+s:
        ChessBoard(tr+s,tc+s,dr,dc,s)
    else:
        Board[tr+s][tc+s]=t
        fill(tr+s,tc+s,t)
        ChessBoard(tr+s,tc+s,tr+s,tc+s,s)

def pre():
    x=2**n
    y=2**n
    xx=np.linspace(x,x+1,10)
    yy=np.linspace(y,y,10)
    yy1=np.linspace(y+1,y+1,10)
    plt.fill_between(xx,yy,yy1,facecolor='white') 
    plt.pause(1)
    pass 

n=int(input())
Board=[[0 for i in range(2**n)] for j in range(2**n)]
x,y=map(int,input().split())
pre() #图像预处理
Board[x][y]=-1
ChessBoard(0,0,x,y,2**n)
for i in range(2**n):
    for j in range(2**n):
        print(Board[i][j],end=' ')
    print()

plt.show()
# n为正方形的阶数 x y为方格点的坐标