结对作业
| 这个作业属于哪个课程 | 班级链接 |
|---|---|
| 这个作业要求在哪里 | 作业链接 |
| 这个作业的目标 | 四则运算生成器+生成应用程序+结对 |
| 项目成员1 | 3119005457 郭炜彬 Github地址 |
| 项目成员2 | 3119005467 刘健君 Github地址 |
| 项目成员3 | 3119005468 刘霖笙 Github地址 |
本次作业,经过软工老师同意,我们项目是三人组队完成的。
1 代码链接(Java)
1.1 Github链接
1.2 可运行的.exe应用程序(Myapp.exe(有图形界面))已经发布至仓库的release包内,运行exe时候文件产生在同级目录下,需要下载整个zip包,因为运行必须要有对应的jre。
2 效能分析
- 全部性能
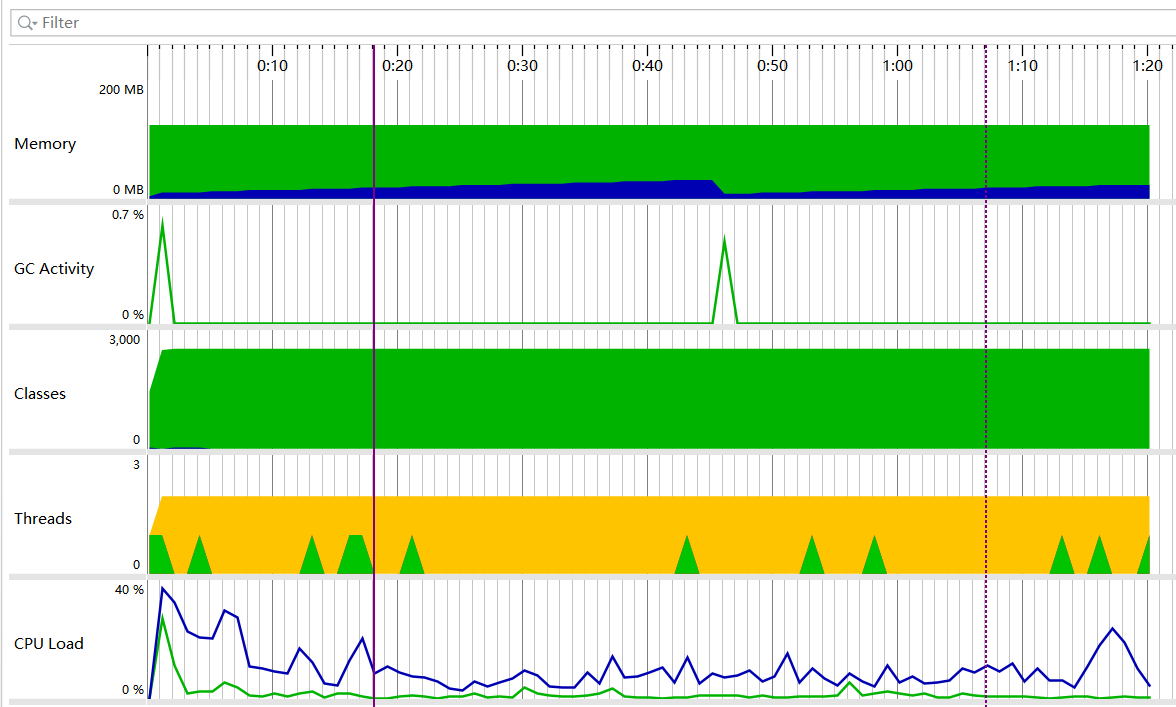
- 类的占用情况

- cpu view

在这个过程中,我们发现生成表达式的类的性能不高,于是我们将原来的算法生成表达式的部分做了改进,利用树的思想,具体的代码和解释在下面会详细讲到,提高了算法的性能;并且在过程中还发现了原来算法的bug,会生成超过三个的表达式,可以说这个算法的改进,既提高了性能,又修改了bug,一举两得!
3 设计实现过程
3.1 主要的包
-
MyApplication包:三个主程序,Main是生成表达式并且计算结果、MainGrade是计算grade、MainGUI是图形界面的生成表达式并且计算结果
-
Util包:项目的最重要部分,分为8个类,下面会详细讲到
3.2 主要的类
-
GenerateUtil类:生成表达式的类,形如“2/5 + 2'1/3 - 1'1/3 =”
-
ReversePolishUtil类:生成逆波兰表达式,以便于进行计算
-
CalculateUtil类:利用栈进行计算,先反转栈,进行计算
-
FractionUtil类:设计分数的+-*/运算
-
FormatUtil类:对结果进行格式化,化简结果,并且进行判断,不能为负
-
ExamineUtil类:对结果进行比较,得出grade
-
FileIOUt il类:将表达式和结果输出指定文件路径
-
类之间的关系图
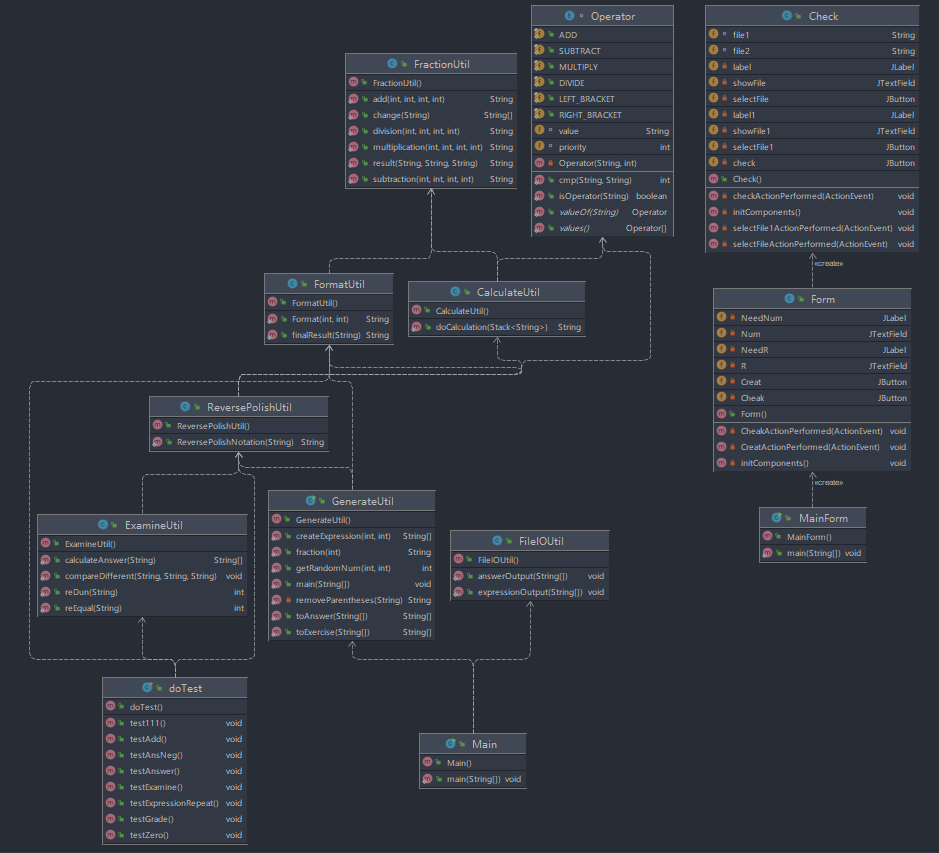
3.3 关键函数
- createExpression()函数,流程图如下
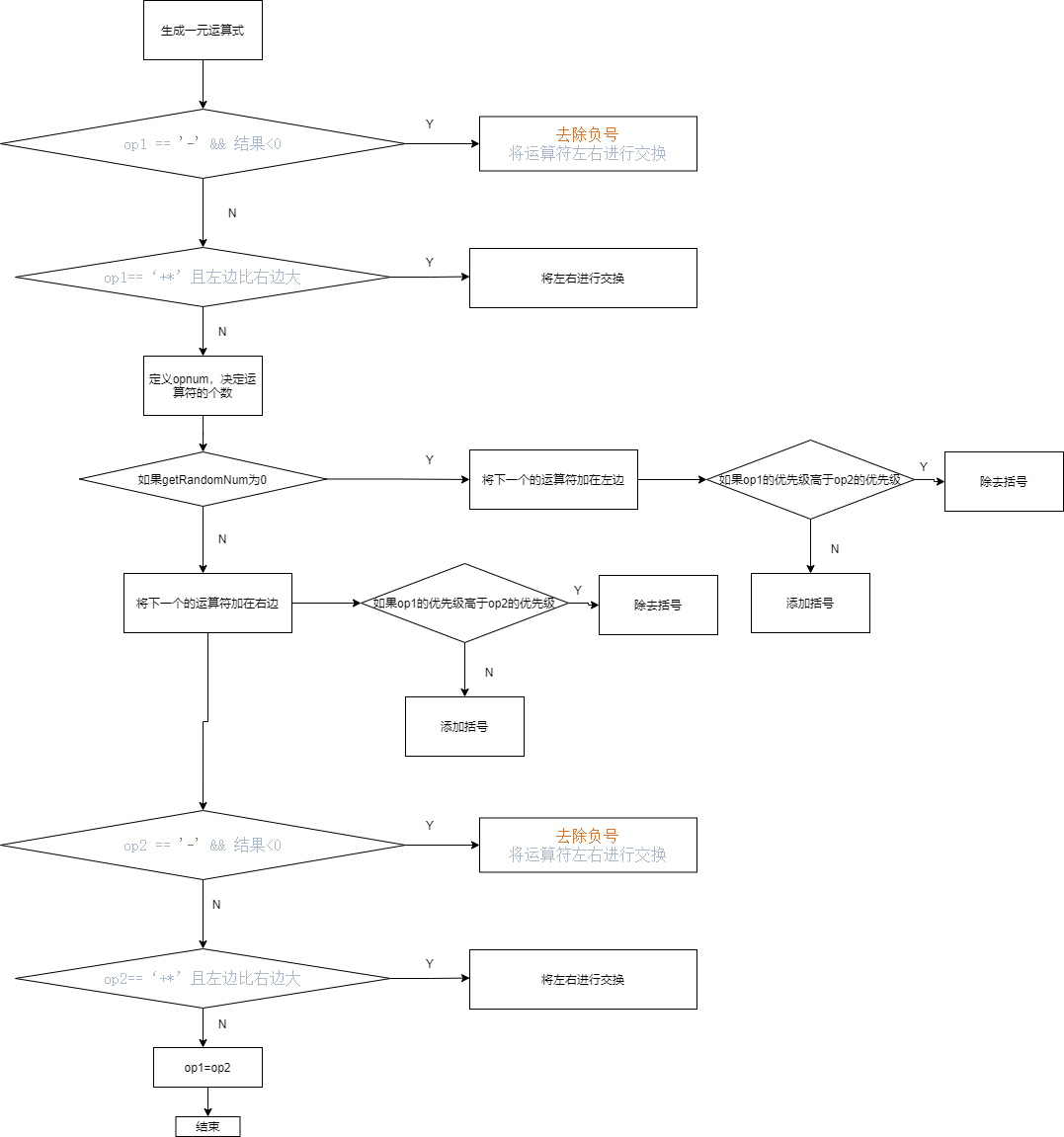
- doCalculation()函数,流程图如下
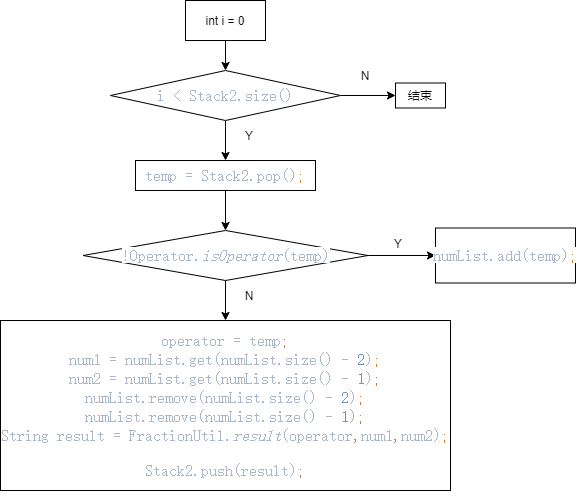
4 代码说明
- createExpression()函数,该类生成表达式比较复杂,下面代码有详细注释,且上面的流程图很好地解释算法的精髓,部分代码如下
public static String[] createExpression(int range, int num) {
//避免重复
HashSet<String> strHashSet = new HashSet<>();
String operator = "+-×÷";//定义四则运算符号,+-*/
Vector<String> expression = new Vector<>();//表达式
Vector<String> result = new Vector<>();
for (int i = 0; i < num; i++) {
try {
//先进行一次一元运算式生成
int opNum = getRandomNum(1,3);
char op1 = operator.charAt(getRandomNum(0, 3));
char op2 = operator.charAt(getRandomNum(0, 3));
String left;
String right;
String valueNow;
left = fraction(range);
// left = String.valueOf(getRandomNum(0,1));
right = fraction(range);
// right = String.valueOf(getRandomNum(0,1));
StringBuilder res = new StringBuilder("( " + left + " " + op1 + " " + right + " )");
valueNow = ReversePolishUtil.ReversePolishNotation(res.toString());
if (op1 == '-' && valueNow.contains("-")) { //交换左右
valueNow = valueNow.substring(1);
res = new StringBuilder("( " + right + " " + op1 + " " + left + " )");
} else if ("+×".contains(String.valueOf(op1)) && //去重
!ReversePolishUtil.ReversePolishNotation(
"( " + left + " - " + right + " )").contains("-")) {
res = new StringBuilder("( " + right + " " + op1 + " " + left + " )");
}
for (int j = 0; j < opNum-1; j++) {
if (getRandomNum(0, 1) == 0) {
left = fraction(range);
// left = String.valueOf(getRandomNum(0,1));
right = res.toString();
if ("×÷".contains(String.valueOf(op1)) && "+-".contains(String.valueOf(op2))) { //若原符号是乘除,新符号是加减,不需要括号 如5+(3*4)应去掉括号
res = new StringBuilder("( " + left + " " + op2 + " " + right.substring(1, res.length() - 1) + " )");
} else
res = new StringBuilder("( " + left + " " + op2 + " " + right + " )"); //其他情况需要括号
} else {
left = res.toString();
right = fraction(range);
// right = String.valueOf(getRandomNum(0,1));
//判断同级
if (("+-".contains(String.valueOf(op1)) && "+-".contains(String.valueOf(op2))) || //若新符号与原符号同级,去掉括号如 (1+2) - 3 应去掉括号
"×÷".contains(String.valueOf(op1))) { //若原符号是乘除,不需要括号,如 (2*2)+1 应去掉括号
res = new StringBuilder("( " + left.substring(1, res.length() - 1) + " " + op2 + " " + right + " )");
} else {
res = new StringBuilder("( " + left + " " + op2 + " " + right + " )");
}
}
valueNow = ReversePolishUtil.ReversePolishNotation(res.toString());
if (op2 == '-' && valueNow.contains("-")) { //交换左右
valueNow = valueNow.substring(1);
res = new StringBuilder("( " + right + " " + op2 + " " + left + " )");
} else if ("+×".contains(String.valueOf(op2)) && //去重
!ReversePolishUtil.ReversePolishNotation(
"( " + left + " - " + right + " )").contains("-")) {
res = new StringBuilder("( " + right + " " + op2 + " " + left + " )");
}
op1 = op2;
op2 = operator.charAt(getRandomNum(0, 3));
}
valueNow = FormatUtil.finalResult(valueNow);
String str = res.substring(1, res.toString().length()-1);
-
ReversePolishNotation()函数,用Stack1栈来存储逆波兰表达式,也称作后缀表达式。
例如:这个a(b-cd)+e式子来说,转成波兰表达式后应该是这样子的:abcd-e+
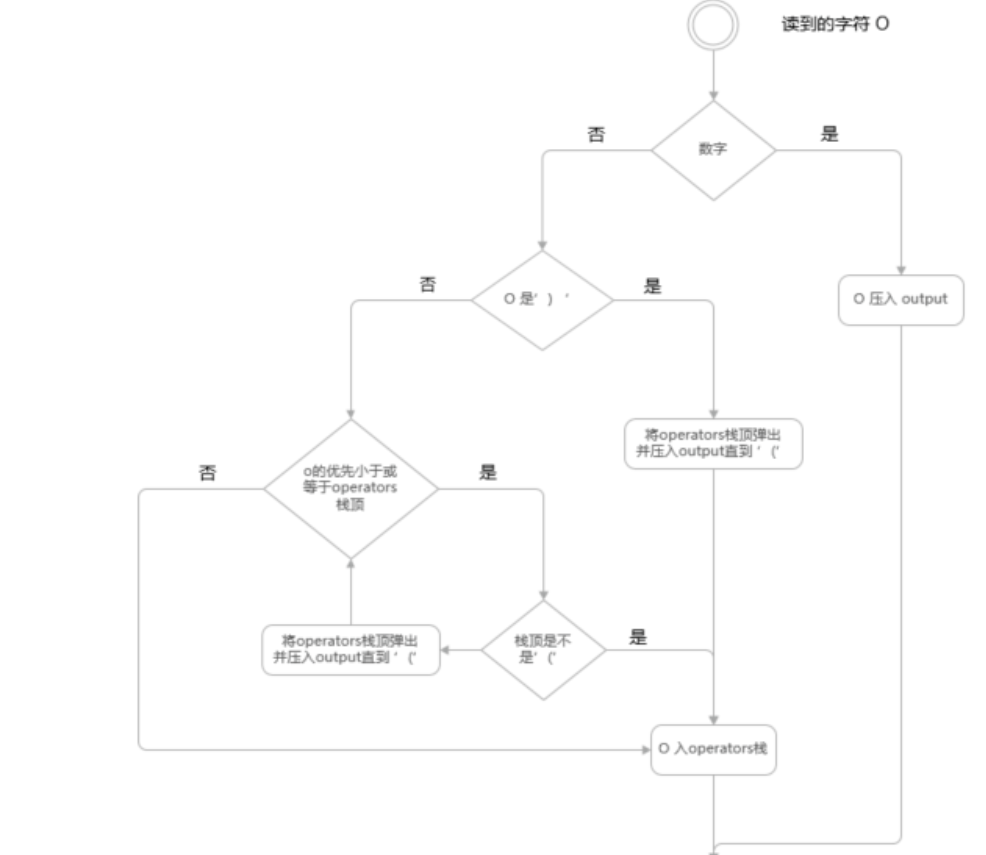
代码如下
Stack<Character> operators = new Stack<>(); //运算符
Stack<String> output = new Stack(); //输出结果
String[] strings = str.split(" ");
int pre = 0;
boolean digital; //是否为数字(只要不是运算符,都是数字),用于截取字符串
int len = strings.length;
int bracket = 0; // 左括号的数量
for (int i = 0; i < len; ) {
pre = i;
digital = false;
//截取数字
while (i < len && !Operator.isOperator(strings[i])) {
i++;
digital = true;
}
if (digital) {
output.push(strings[i-1]);
} else {
String o = strings[i++]; //运算符
if (o.equals("(")) {
bracket++;
}
if (bracket > 0) {
if (o.equals(")")) {
while (!operators.empty()) {
char top = operators.pop();
if (top == '(') {
break;
}
output.push(String.valueOf(top));
}
bracket--;
} else {
//如果栈顶为 ( ,则直接添加,不顾其优先级
//如果之前有 ( ,但是 ( 不在栈顶,则需判断其优先级,如果优先级比栈顶的低,则依次出栈
while (!operators.empty() && operators.peek() != '(' && Operator.cmp(o, String.valueOf(operators.peek())) <= 0) {
output.push(String.valueOf(operators.pop()));
}
operators.push(o.charAt(0));
}
} else {
while (!operators.empty() && Operator.cmp(o, String.valueOf(operators.peek())) <= 0) {
output.push(String.valueOf(operators.pop()));
}
operators.push(o.charAt(0));
}
}
}
-
doCalculation()函数,运用两个栈,反转逆波兰表达式的栈Stack1,得到Stack2,pop()出栈顶元素,如果是运算符,就去前numList中前两个元素通过FractionUtil.result函数进行计算,如果不是,则添加进去numList中。
代码如下
List<String> numList = new ArrayList<>(); Stack<String> Stack2 = new Stack(); String operator = ""; String num1 = ""; String num2 = ""; String temp = ""; //将stack1放入stack2 for (int i = 0; i < Stack1.size();) { Stack2.push(Stack1.pop()); } for (int i = 0; i < Stack2.size();) { temp = Stack2.pop(); //判断是否运算符 if(!Operator.isOperator(temp)){ numList.add(temp); }else{ operator = temp; num1 = numList.get(numList.size() - 2); num2 = numList.get(numList.size() - 1); numList.remove(numList.size() - 2); numList.remove(numList.size() - 1); String result = FractionUtil.result(operator,num1,num2); if(result.contains("-")){ throw new Exception(); }else{ Stack2.push(result); } } } return temp;
5 测试运行
- 要求1、2:使用 -n 参数控制生成题目的个数,使用 -r 参数控制题目中数值
- 命令行
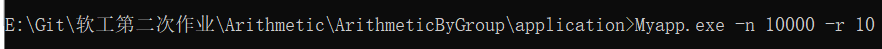
生成的文件在application目录下的exercises.txt和answers.txt文件中
-
界面
-

-
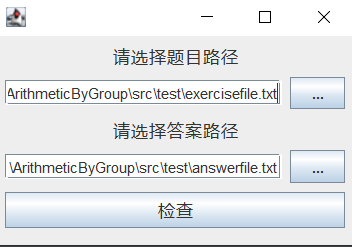
生成文件在

内容为


- 要求3:生成的题目中计算过程不能产生负数,代码如下
String result = FractionUtil.result(operator,num1,num2);
if(result.contains("-")){
throw new Exception();
}else{
Stack2.push(result);
}
单元测试
//测试结果为负
@Test
public void testAnsNeg(){
String str = "3 - 4";
try {
ReversePolishUtil.ReversePolishNotation(str);
} catch (Exception e) {
e.printStackTrace();
System.out.println("测试结果为负,不符合要求!");
}
}
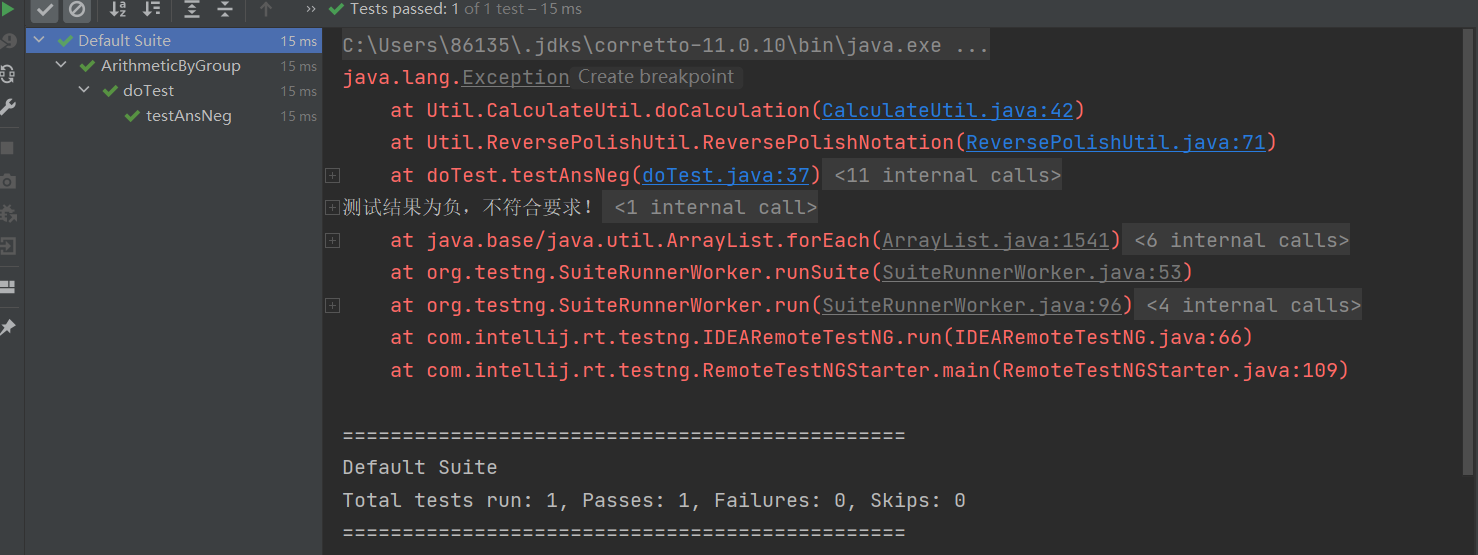
-
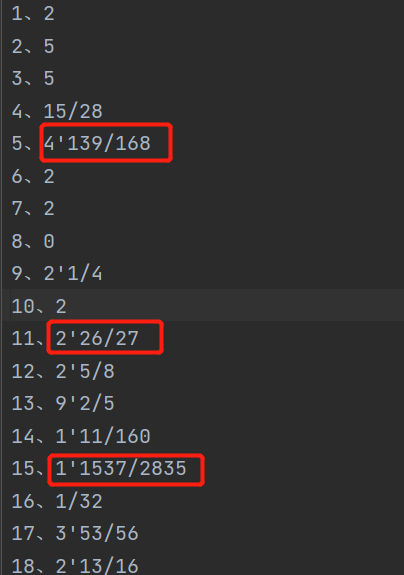
要求4:生成的题目中如果存在形如e1÷ e2的子表达式,那么*其结果应是真分数*
代码中我们都是用真分数进行计算的
-
要求5:每道题目中出现的运算符个数不超过3个
从Exercises.txt文件中可以看出,当生成10000个表达式时,不会超过三个运算符以上的表达式
从代码中,我们是按照随机数生成确定运算符的个数,在generateUtil类中,定义int opNum = getRandomNum(1,3);,可以看出,不会超过三个运算符
-
要求6:不会产生重复的表达式
从代码的角度可以看出,我们运用二叉树的构造思想,从左右进行插入,将结果是小的放在左边,结果大的放在右边,保证输出只能有一种情况,来满足题目的要求。
从结果的角度,我们应用0,1和四则运算符进行测试,一共会生成11种不重复的表达式,程序代码及运行的结果如下:
public static void main(String[] args) throws Exception { String[] strings = GenerateUtil.createExpression(10,11); for (int i = 0; i < strings.length; i++) { System.out.println(i+1 + " 、 " +strings[i]); } }结果:
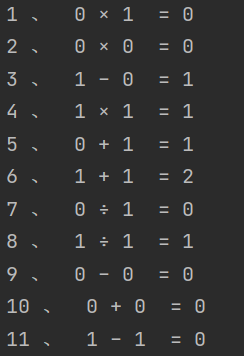
如果num范围大于11,就会陷入死循环,这是因为我们hashset来存储不重复的数据,代码如下:
//如果生成的表达式没有在hashset中,就说明没有重复
if (!strHashSet.contains(str)) {
strHashSet.add(str);
result.add(valueNow);
expression.add(str + " = " + valueNow);
} else i--;
-
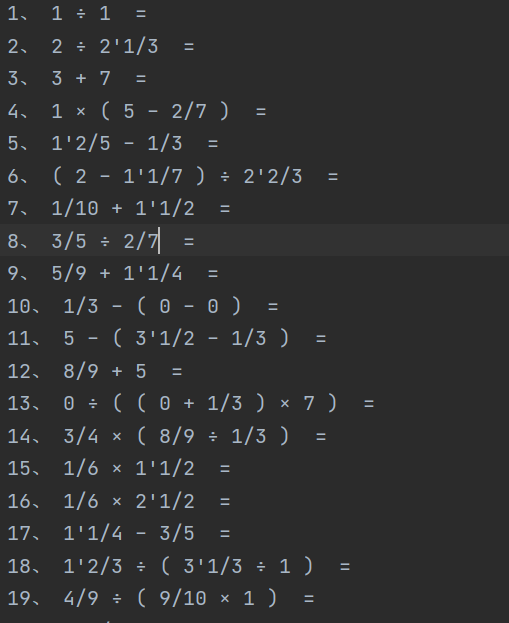
要求7:生成的题目存入执行程序的当前目录下的Exercises.txt文件,在生成题目的同时,计算出所有题目的答案,并存入执行程序的当前目录下的Answers.txt文件
将exercises.txt和answers.txt存储在src目录下,格式满足要求

-
要求8:程序应能支持一万道题目的生成,满足。
-
要求9:程序支持对给定的题目文件和答案文件,判定答案中的对错并进行数量统计
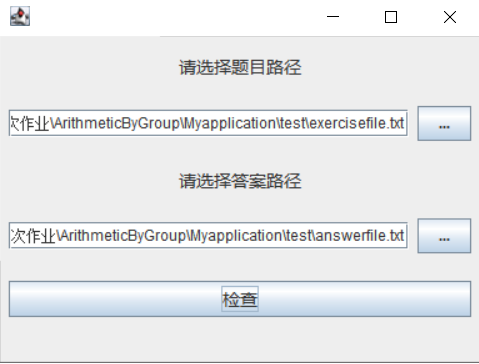

生成Grade.txt文本,并且没有错误日志,说明运行没有错误,结果如下图所示,结果没问题,是正确的!

6 PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时 | 实际耗时(分钟) |
|---|---|---|---|
| ·Planning | · 计划 | 45 | 45 |
| · Estimate | · 估计这个任务需要多少时间 | 45 | 45 |
| ·Development | 开发 | 350 | 820 |
| · Analysis | · 需求分析 (包括学习新技术) | 20 | 90 |
| · Design Spec | · 生成设计文档 | 30 | 50 |
| · Design Review | · 设计复审 | 15 | 20 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | 20 |
| · Design | · 具体设计 | 50 | 60 |
| · Coding | · 具体编码 | 150 | 500 |
| · Code Review | · 代码复审 | 20 | 20 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 45 | 60 |
| · Reporting | · 报告 | 85 | 95 |
| · Test Repor | · 测试报告 | 20 | 20 |
| · Size Measurement | · 计算工作量 | 15 | 15 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 50 | 60 |
| · 合计 | 475 | 960 |
7 单元测试
本次单元测试设置了十个单元测试用例,具体设置如下:
计算测试
-
输入带括号加法,检测结果
-
输入带括号减法,检测结果
-
输入带括号乘法,检测结果
-
输入带括号除法,检测结果
-
输入复杂的四则运算,检测结果
-
输入带分数的运算,检测结果
特殊情况测试
- 测试除数为0的情况
- 测试结果为负的情况
- 测试分数的约分功能
功能测试
- 测试能否正确判断答案对错
- 测试能否真正生成四则运算题目
测试结果如下:
计算测试用例

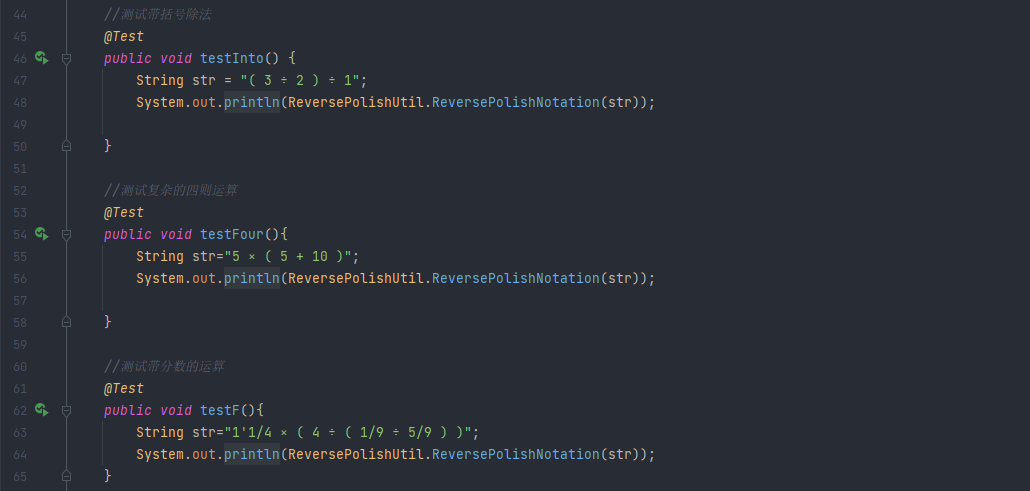
特殊情况测试:
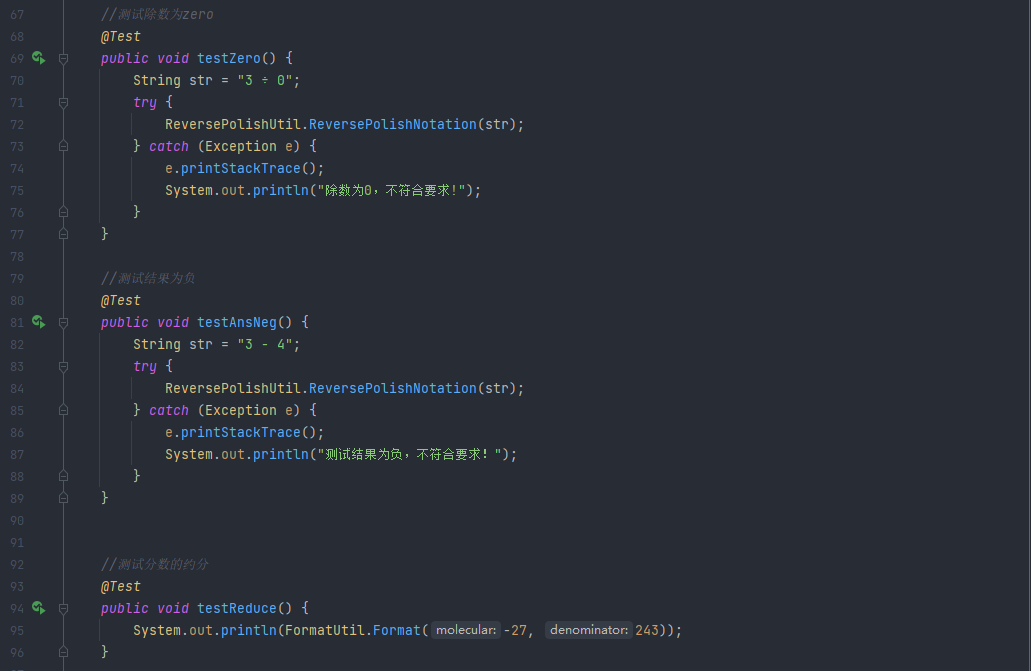
功能测试:
可以得到11个测试用例全部通过:
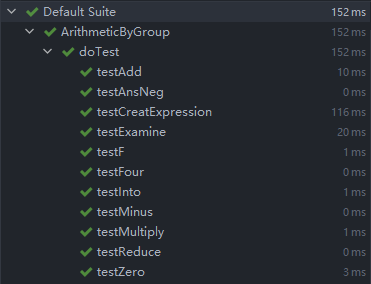
8 代码审查
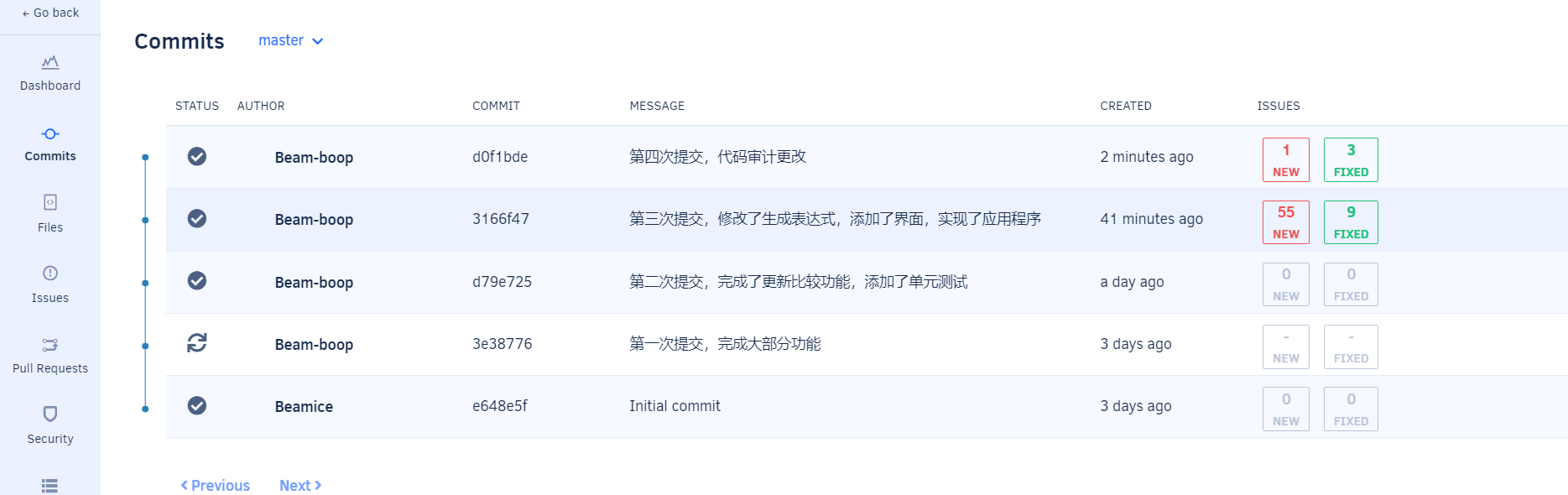
代码审查后发现很多错误,都是命名不规范,修改后剩下一些大错误,但是是在jre里面的,所以不给予修改。
9 项目小结
成员1:郭炜彬小结
本次项目是由三个人完成的,个人认为试一次成功的结对作业,学习到了很多东西。
1.有学习了新的技能,打包成jar包后,生成exe应用程序
2.在队友的指导下,学会用图形界面做简单界面,后面还需要继续努力学习
3.最重要的还是和队友的合作,说句实话,结对作业比个人作业难,在我个人看来,难不是难在题目的难度,因为很多都可以在网上找得到代码(不过我们的代码大部分是自己写的,少部分借鉴别人),难在和队友的合作上,因为都是第一次合作,没有经验,不知道从何下手,所以我们就先去借鉴别人的代码,学习别人的思路,收集资料,然后再进行分工合作;在合作中,发现我们对于类和方法的命名习惯不一样,以至于每一次将自己的代码给到别人,需要去更改命名,就有点......,最后我们一起在同一台电脑上进行操作,将自己的思想进行充分的交流,最后才能完成这份看似容易,实则不易的项目作业,也想对组内的成员说声辛苦啦!!!
成员2:刘健君小结
在这次结队项目中,我体会到了合作的重要性。不同于单枪匹马,我们需要将任务及要实现的需求分为几个部分,由每个人完成各自的部分,这也需要我们更加注意代码的规范性。在实现各种功能的过程中,我也学习到了,注意到了以前没有注意到的细节。总的来说,这一次结对作业是一次特别的体验,从中我也学习到了很多,也想对组内的成员说一声辛苦了~~
成员3:刘霖笙小结
首先我十分感谢我的两位队友在这次项目中对我的帮助,由于我本人使用的编程语言限制原因,无法和许多同学进行合作,但是我的两位队友不嫌弃我,与我结对。而我本人在本次项目中的能力也十分有限,只能对思路、资料进行一个整理,在git管理使用上的有限帮助,但是还是学到了很多东西。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号